First-Order Rewritability of Frontier-Guarded Ontology-Mediated Queries

We focus on ontology-mediated queries (OMQs) based on (frontier-)guarded existential rules and (unions of) conjunctive queries, and we investigate the problem of FO-rewritability, i.e., whether an OMQ can be rewritten as a first-order query. We adopt two different approaches. The first approach employs standard two-way alternating parity tree automata. Although it does not lead to a tight complexity bound, it provides a transparent solution based on widely known tools. The second approach relies on a sophisticated automata model, known as cost automata. This allows us to show that our problem is 2ExpTime-complete. In both approaches, we provide semantic characterizations of FO-rewritability that are of independent interest.

The Space-Efficient Core of Vadalog

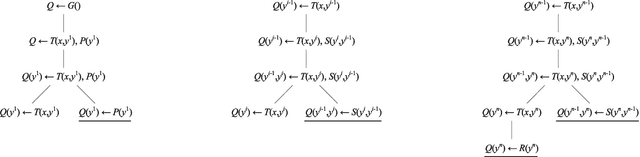
Vadalog is a system for performing complex reasoning tasks such as those required in advanced knowledge graphs. The logical core of the underlying Vadalog language is the warded fragment of tuple-generating dependencies (TGDs). This formalism ensures tractable reasoning in data complexity, while a recent analysis focusing on a practical implementation led to the reasoning algorithm around which the Vadalog system is built. A fundamental question that has emerged in the context of Vadalog is the following: can we limit the recursion allowed by wardedness in order to obtain a formalism that provides a convenient syntax for expressing useful recursive statements, and at the same time achieves space-efficiency? After analyzing several real-life examples of warded sets of TGDs provided by our industrial partners, as well as recent benchmarks, we observed that recursion is often used in a restricted way: the body of a TGD contains at most one atom whose predicate is mutually recursive with a predicate in the head. We show that this type of recursion, known as piece-wise linear in the Datalog literature, is the answer to our main question. We further show that piece-wise linear recursion alone, without the wardedness condition, is not enough as it leads to the undecidability of reasoning. We finally study the relative expressiveness of the query languages based on (piece-wise linear) warded sets of TGDs.

Containment for Rule-Based Ontology-Mediated Queries

Many efforts have been dedicated to identifying restrictions on ontologies expressed as tuple-generating dependencies (tgds), a.k.a. existential rules, that lead to the decidability for the problem of answering ontology-mediated queries (OMQs). This has given rise to three families of formalisms: guarded, non-recursive, and sticky sets of tgds. In this work, we study the containment problem for OMQs expressed in such formalisms, which is a key ingredient for solving static analysis tasks associated with them. Our main contribution is the development of specially tailored techniques for OMQ containment under the classes of tgds stated above. This enables us to obtain sharp complexity bounds for the problems at hand, which in turn allow us to delimitate its practical applicability. We also apply our techniques to pinpoint the complexity of problems associated with two emerging applications of OMQ containment: distribution over components and UCQ rewritability of OMQs.