A Symbolic Language for Interpreting Decision Trees

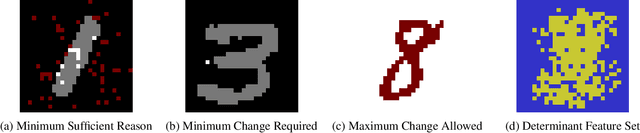
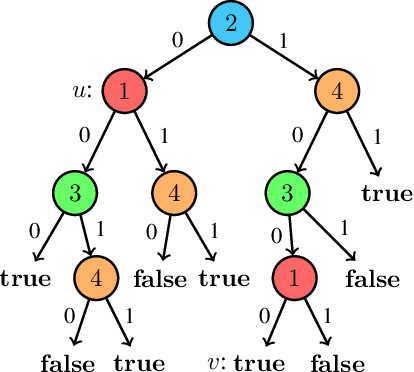
The recent development of formal explainable AI has disputed the folklore claim that "decision trees are readily interpretable models", showing different interpretability queries that are computationally hard on decision trees, as well as proposing different methods to deal with them in practice. Nonetheless, no single explainability query or score works as a "silver bullet" that is appropriate for every context and end-user. This naturally suggests the possibility of "interpretability languages" in which a wide variety of queries can be expressed, giving control to the end-user to tailor queries to their particular needs. In this context, our work presents ExplainDT, a symbolic language for interpreting decision trees. ExplainDT is rooted in a carefully constructed fragment of first-ordered logic that we call StratiFOILed. StratiFOILed balances expressiveness and complexity of evaluation, allowing for the computation of many post-hoc explanations--both local (e.g., abductive and contrastive explanations) and global ones (e.g., feature relevancy)--while remaining in the Boolean Hierarchy over NP. Furthermore, StratiFOILed queries can be written as a Boolean combination of NP-problems, thus allowing us to evaluate them in practice with a constant number of calls to a SAT solver. On the theoretical side, our main contribution is an in-depth analysis of the expressiveness and complexity of StratiFOILed, while on the practical side, we provide an optimized implementation for encoding StratiFOILed queries as propositional formulas, together with an experimental study on its efficiency.

Logical Languages Accepted by Transformer Encoders with Hard Attention

We contribute to the study of formal languages that can be recognized by transformer encoders. We focus on two self-attention mechanisms: (1) UHAT (Unique Hard Attention Transformers) and (2) AHAT (Average Hard Attention Transformers). UHAT encoders are known to recognize only languages inside the circuit complexity class ${\sf AC}^0$, i.e., accepted by a family of poly-sized and depth-bounded boolean circuits with unbounded fan-ins. On the other hand, AHAT encoders can recognize languages outside ${\sf AC}^0$), but their expressive power still lies within the bigger circuit complexity class ${\sf TC}^0$, i.e., ${\sf AC}^0$-circuits extended by majority gates. We first show a negative result that there is an ${\sf AC}^0$-language that cannot be recognized by an UHAT encoder. On the positive side, we show that UHAT encoders can recognize a rich fragment of ${\sf AC}^0$-languages, namely, all languages definable in first-order logic with arbitrary unary numerical predicates. This logic, includes, for example, all regular languages from ${\sf AC}^0$. We then show that AHAT encoders can recognize all languages of our logic even when we enrich it with counting terms. We apply these results to derive new results on the expressive power of UHAT and AHAT up to permutation of letters (a.k.a. Parikh images).

Weisfeiler and Leman Go Relational

Knowledge graphs, modeling multi-relational data, improve numerous applications such as question answering or graph logical reasoning. Many graph neural networks for such data emerged recently, often outperforming shallow architectures. However, the design of such multi-relational graph neural networks is ad-hoc, driven mainly by intuition and empirical insights. Up to now, their expressivity, their relation to each other, and their (practical) learning performance is poorly understood. Here, we initiate the study of deriving a more principled understanding of multi-relational graph neural networks. Namely, we investigate the limitations in the expressive power of the well-known Relational GCN and Compositional GCN architectures and shed some light on their practical learning performance. By aligning both architectures with a suitable version of the Weisfeiler-Leman test, we establish under which conditions both models have the same expressive power in distinguishing non-isomorphic (multi-relational) graphs or vertices with different structural roles. Further, by leveraging recent progress in designing expressive graph neural networks, we introduce the $k$-RN architecture that provably overcomes the expressiveness limitations of the above two architectures. Empirically, we confirm our theoretical findings in a vertex classification setting over small and large multi-relational graphs.

First-Order Rewritability of Frontier-Guarded Ontology-Mediated Queries

We focus on ontology-mediated queries (OMQs) based on (frontier-)guarded existential rules and (unions of) conjunctive queries, and we investigate the problem of FO-rewritability, i.e., whether an OMQ can be rewritten as a first-order query. We adopt two different approaches. The first approach employs standard two-way alternating parity tree automata. Although it does not lead to a tight complexity bound, it provides a transparent solution based on widely known tools. The second approach relies on a sophisticated automata model, known as cost automata. This allows us to show that our problem is 2ExpTime-complete. In both approaches, we provide semantic characterizations of FO-rewritability that are of independent interest.

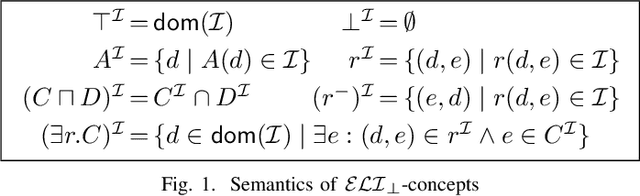
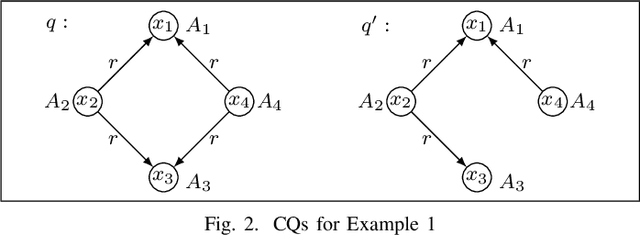
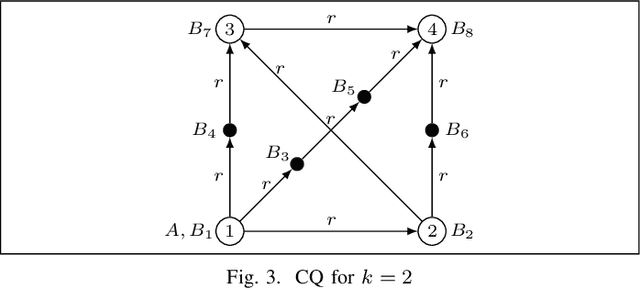
When is Ontology-Mediated Querying Efficient?

In ontology-mediated querying, description logic (DL) ontologies are used to enrich incomplete data with domain knowledge which results in more complete answers to queries. However, the evaluation of ontology-mediated queries (OMQs) over relational databases is computationally hard. This raises the question when OMQ evaluation is efficient, in the sense of being tractable in combined complexity or fixed-parameter tractable. We study this question for a range of ontology-mediated query languages based on several important and widely-used DLs, using unions of conjunctive queries as the actual queries. For the DL ELHI extended with the bottom concept, we provide a characterization of the classes of OMQs that are fixed-parameter tractable. For its fragment EL extended with domain and range restrictions and the bottom concept (which restricts the use of inverse roles), we provide a characterization of the classes of OMQs that are tractable in combined complexity. Both results are in terms of equivalence to OMQs of bounded tree width and rest on a reasonable assumption from parameterized complexity theory. They are similar in spirit to Grohe's seminal characterization of the tractable classes of conjunctive queries over relational databases. We further study the complexity of the meta problem of deciding whether a given OMQ is equivalent to an OMQ of bounded tree width, providing several completeness results that range from NP to 2ExpTime, depending on the DL used. We also consider the DL-Lite family of DLs, including members that admit functional roles.

The Limits of Efficiency for Open- and Closed-World Query Evaluation Under Guarded TGDs

Ontology-mediated querying and querying in the presence of constraints are two key database problems where tuple-generating dependencies (TGDs) play a central role. In ontology-mediated querying, TGDs can formalize the ontology and thus derive additional facts from the given data, while in querying in the presence of constraints, they restrict the set of admissible databases. In this work, we study the limits of efficient query evaluation in the context of the above two problems, focussing on guarded and frontier-guarded TGDs and on UCQs as the actual queries. We show that a class of ontology-mediated queries (OMQs) based on guarded TGDs can be evaluated in FPT iff the OMQs in the class are equivalent to OMQs in which the actual query has bounded treewidth, up to some reasonable assumptions. For querying in the presence of constraints, we consider classes of constraint-query specifications (CQSs) that bundle a set of constraints with an actual query. We show a dichotomy result for CQSs based on guarded TGDs that parallels the one for OMQs except that, additionally, FPT coincides with PTime combined complexity. The proof is based on a novel connection between OMQ and CQS evaluation. Using a direct proof, we also show a similar dichotomy result, again up to some reasonable assumptions, for CQSs based on frontier-guarded TGDs with a bounded number of atoms in TGD heads. Our results on CQSs can be viewed as extensions of Grohe's well-known characterization of the tractable classes of CQs (without constraints). Like Grohe's characterization, all the above results assume that the arity of relation symbols is bounded by a constant. We also study the associated meta problems, i.e., whether a given OMQ or CQS is equivalent to one in which the actual query has bounded treewidth.

Containment for Rule-Based Ontology-Mediated Queries

Many efforts have been dedicated to identifying restrictions on ontologies expressed as tuple-generating dependencies (tgds), a.k.a. existential rules, that lead to the decidability for the problem of answering ontology-mediated queries (OMQs). This has given rise to three families of formalisms: guarded, non-recursive, and sticky sets of tgds. In this work, we study the containment problem for OMQs expressed in such formalisms, which is a key ingredient for solving static analysis tasks associated with them. Our main contribution is the development of specially tailored techniques for OMQ containment under the classes of tgds stated above. This enables us to obtain sharp complexity bounds for the problems at hand, which in turn allow us to delimitate its practical applicability. We also apply our techniques to pinpoint the complexity of problems associated with two emerging applications of OMQ containment: distribution over components and UCQ rewritability of OMQs.