Explaining k-Nearest Neighbors: Abductive and Counterfactual Explanations

Despite the wide use of $k$-Nearest Neighbors as classification models, their explainability properties remain poorly understood from a theoretical perspective. While nearest neighbors classifiers offer interpretability from a "data perspective", in which the classification of an input vector $\bar{x}$ is explained by identifying the vectors $\bar{v}_1, \ldots, \bar{v}_k$ in the training set that determine the classification of $\bar{x}$, we argue that such explanations can be impractical in high-dimensional applications, where each vector has hundreds or thousands of features and it is not clear what their relative importance is. Hence, we focus on understanding nearest neighbor classifications through a "feature perspective", in which the goal is to identify how the values of the features in $\bar{x}$ affect its classification. Concretely, we study abductive explanations such as "minimum sufficient reasons", which correspond to sets of features in $\bar{x}$ that are enough to guarantee its classification, and "counterfactual explanations" based on the minimum distance feature changes one would have to perform in $\bar{x}$ to change its classification. We present a detailed landscape of positive and negative complexity results for counterfactual and abductive explanations, distinguishing between discrete and continuous feature spaces, and considering the impact of the choice of distance function involved. Finally, we show that despite some negative complexity results, Integer Quadratic Programming and SAT solving allow for computing explanations in practice.

Probabilistic Explanations for Linear Models

Formal XAI is an emerging field that focuses on providing explanations with mathematical guarantees for the decisions made by machine learning models. A significant amount of work in this area is centered on the computation of "sufficient reasons". Given a model $M$ and an input instance $\vec{x}$, a sufficient reason for the decision $M(\vec{x})$ is a subset $S$ of the features of $\vec{x}$ such that for any instance $\vec{z}$ that has the same values as $\vec{x}$ for every feature in $S$, it holds that $M(\vec{x}) = M(\vec{z})$. Intuitively, this means that the features in $S$ are sufficient to fully justify the classification of $\vec{x}$ by $M$. For sufficient reasons to be useful in practice, they should be as small as possible, and a natural way to reduce the size of sufficient reasons is to consider a probabilistic relaxation; the probability of $M(\vec{x}) = M(\vec{z})$ must be at least some value $\delta \in (0,1]$, for a random instance $\vec{z}$ that coincides with $\vec{x}$ on the features in $S$. Computing small $\delta$-sufficient reasons ($\delta$-SRs) is known to be a theoretically hard problem; even over decision trees--traditionally deemed simple and interpretable models--strong inapproximability results make the efficient computation of small $\delta$-SRs unlikely. We propose the notion of $(\delta, \epsilon)$-SR, a simple relaxation of $\delta$-SRs, and show that this kind of explanation can be computed efficiently over linear models.

A Symbolic Language for Interpreting Decision Trees

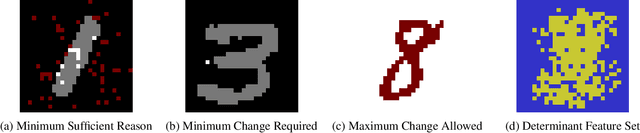
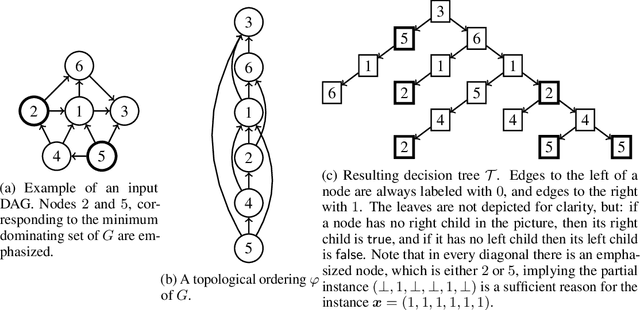
The recent development of formal explainable AI has disputed the folklore claim that "decision trees are readily interpretable models", showing different interpretability queries that are computationally hard on decision trees, as well as proposing different methods to deal with them in practice. Nonetheless, no single explainability query or score works as a "silver bullet" that is appropriate for every context and end-user. This naturally suggests the possibility of "interpretability languages" in which a wide variety of queries can be expressed, giving control to the end-user to tailor queries to their particular needs. In this context, our work presents ExplainDT, a symbolic language for interpreting decision trees. ExplainDT is rooted in a carefully constructed fragment of first-ordered logic that we call StratiFOILed. StratiFOILed balances expressiveness and complexity of evaluation, allowing for the computation of many post-hoc explanations--both local (e.g., abductive and contrastive explanations) and global ones (e.g., feature relevancy)--while remaining in the Boolean Hierarchy over NP. Furthermore, StratiFOILed queries can be written as a Boolean combination of NP-problems, thus allowing us to evaluate them in practice with a constant number of calls to a SAT solver. On the theoretical side, our main contribution is an in-depth analysis of the expressiveness and complexity of StratiFOILed, while on the practical side, we provide an optimized implementation for encoding StratiFOILed queries as propositional formulas, together with an experimental study on its efficiency.

The Packing Chromatic Number of the Infinite Square Grid is 15

A packing $k$-coloring is a natural variation on the standard notion of graph $k$-coloring, where vertices are assigned numbers from $\{1, \ldots, k\}$, and any two vertices assigned a common color $c \in \{1, \ldots, k\}$ need to be at a distance greater than $c$ (as opposed to $1$, in standard graph colorings). Despite a sequence of incremental work, determining the packing chromatic number of the infinite square grid has remained an open problem since its introduction in 2002. We culminate the search by proving this number to be 15. We achieve this result by improving the best-known method for this problem by roughly two orders of magnitude. The most important technique to boost performance is a novel, surprisingly effective propositional encoding for packing colorings. Additionally, we developed an alternative symmetry-breaking method. Since both new techniques are more complex than existing techniques for this problem, a verified approach is required to trust them. We include both techniques in a proof of unsatisfiability, reducing the trusted core to the correctness of the direct encoding.

Foundations of Symbolic Languages for Model Interpretability

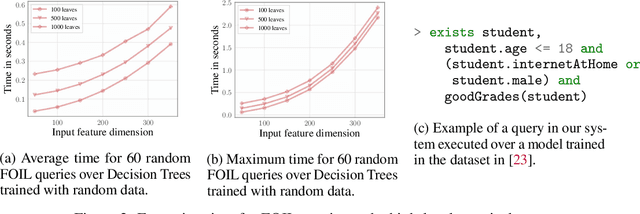
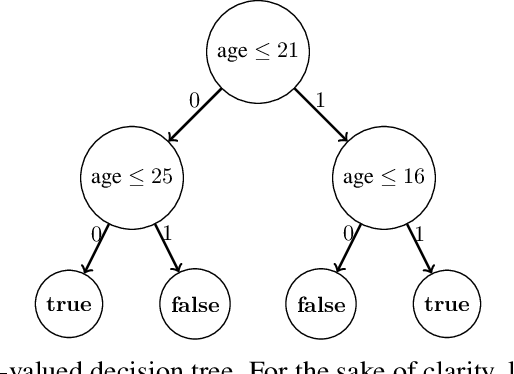
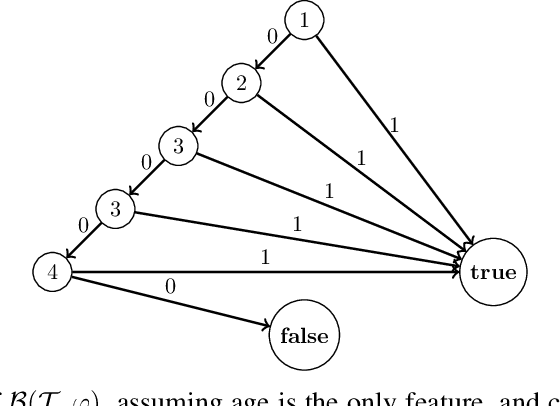
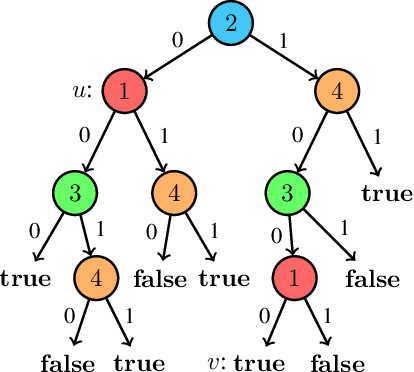
Several queries and scores have recently been proposed to explain individual predictions over ML models. Given the need for flexible, reliable, and easy-to-apply interpretability methods for ML models, we foresee the need for developing declarative languages to naturally specify different explainability queries. We do this in a principled way by rooting such a language in a logic, called FOIL, that allows for expressing many simple but important explainability queries, and might serve as a core for more expressive interpretability languages. We study the computational complexity of FOIL queries over two classes of ML models often deemed to be easily interpretable: decision trees and OBDDs. Since the number of possible inputs for an ML model is exponential in its dimension, the tractability of the FOIL evaluation problem is delicate but can be achieved by either restricting the structure of the models or the fragment of FOIL being evaluated. We also present a prototype implementation of FOIL wrapped in a high-level declarative language and perform experiments showing that such a language can be used in practice.

Model Interpretability through the Lens of Computational Complexity

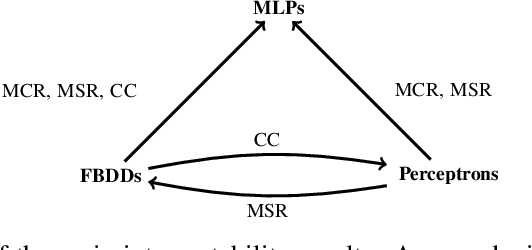
In spite of several claims stating that some models are more interpretable than others -- e.g., "linear models are more interpretable than deep neural networks" -- we still lack a principled notion of interpretability to formally compare among different classes of models. We make a step towards such a notion by studying whether folklore interpretability claims have a correlate in terms of computational complexity theory. We focus on local post-hoc explainability queries that, intuitively, attempt to answer why individual inputs are classified in a certain way by a given model. In a nutshell, we say that a class $\mathcal{C}_1$ of models is more interpretable than another class $\mathcal{C}_2$, if the computational complexity of answering post-hoc queries for models in $\mathcal{C}_2$ is higher than for those in $\mathcal{C}_1$. We prove that this notion provides a good theoretical counterpart to current beliefs on the interpretability of models; in particular, we show that under our definition and assuming standard complexity-theoretical assumptions (such as P$\neq$NP), both linear and tree-based models are strictly more interpretable than neural networks. Our complexity analysis, however, does not provide a clear-cut difference between linear and tree-based models, as we obtain different results depending on the particular post-hoc explanations considered. Finally, by applying a finer complexity analysis based on parameterized complexity, we are able to prove a theoretical result suggesting that shallow neural networks are more interpretable than deeper ones.