A Linear Weight Transfer Rule for Local Search

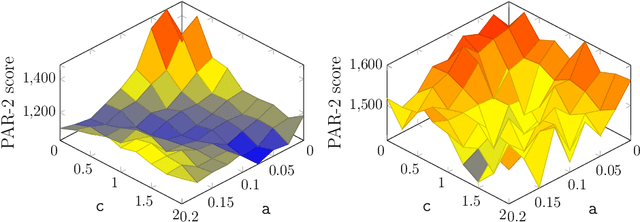
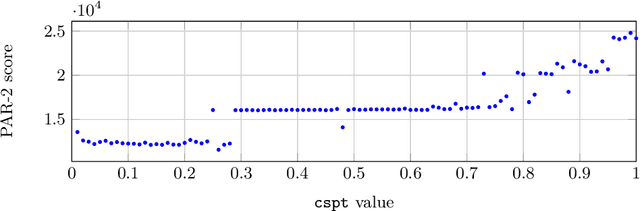
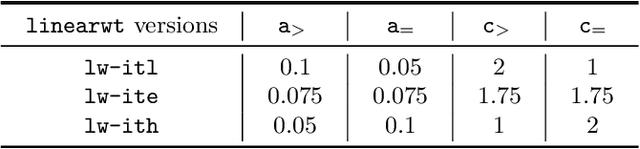
The Divide and Distribute Fixed Weights algorithm (ddfw) is a dynamic local search SAT-solving algorithm that transfers weight from satisfied to falsified clauses in local minima. ddfw is remarkably effective on several hard combinatorial instances. Yet, despite its success, it has received little study since its debut in 2005. In this paper, we propose three modifications to the base algorithm: a linear weight transfer method that moves a dynamic amount of weight between clauses in local minima, an adjustment to how satisfied clauses are chosen in local minima to give weight, and a weighted-random method of selecting variables to flip. We implemented our modifications to ddfw on top of the solver yalsat. Our experiments show that our modifications boost the performance compared to the original ddfw algorithm on multiple benchmarks, including those from the past three years of SAT competitions. Moreover, our improved solver exclusively solves hard combinatorial instances that refute a conjecture on the lower bound of two Van der Waerden numbers set forth by Ahmed et al. (2014), and it performs well on a hard graph-coloring instance that has been open for over three decades.

The Packing Chromatic Number of the Infinite Square Grid is 15

A packing $k$-coloring is a natural variation on the standard notion of graph $k$-coloring, where vertices are assigned numbers from $\{1, \ldots, k\}$, and any two vertices assigned a common color $c \in \{1, \ldots, k\}$ need to be at a distance greater than $c$ (as opposed to $1$, in standard graph colorings). Despite a sequence of incremental work, determining the packing chromatic number of the infinite square grid has remained an open problem since its introduction in 2002. We culminate the search by proving this number to be 15. We achieve this result by improving the best-known method for this problem by roughly two orders of magnitude. The most important technique to boost performance is a novel, surprisingly effective propositional encoding for packing colorings. Additionally, we developed an alternative symmetry-breaking method. Since both new techniques are more complex than existing techniques for this problem, a verified approach is required to trust them. We include both techniques in a proof of unsatisfiability, reducing the trusted core to the correctness of the direct encoding.

Concurrent Cube-and-Conquer

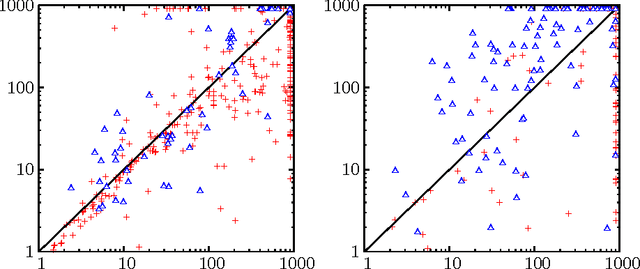
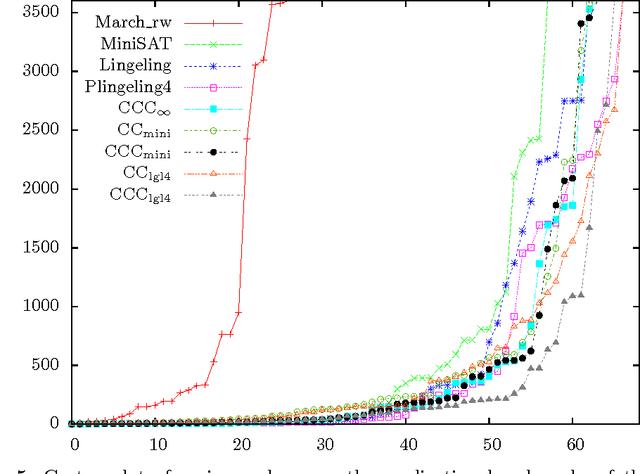
Recent work introduced the cube-and-conquer technique to solve hard SAT instances. It partitions the search space into cubes using a lookahead solver. Each cube is tackled by a conflict-driven clause learning (CDCL) solver. Crucial for strong performance is the cutoff heuristic that decides when to switch from lookahead to CDCL. Yet, this offline heuristic is far from ideal. In this paper, we present a novel hybrid solver that applies the cube and conquer steps simultaneously. A lookahead and a CDCL solver work together on each cube, while communication is restricted to synchronization. Our concurrent cube-and-conquer solver can solve many instances faster than pure lookahead, pure CDCL and offline cube-and-conquer, and can abort early in favor of a pure CDCL search if an instance is not suitable for cube-and-conquer techniques.