A Linear Weight Transfer Rule for Local Search

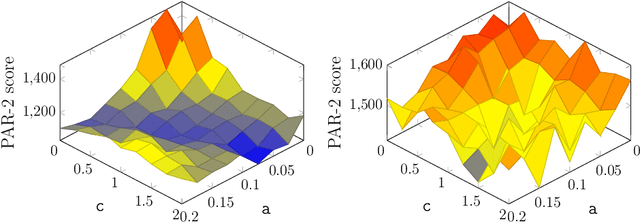
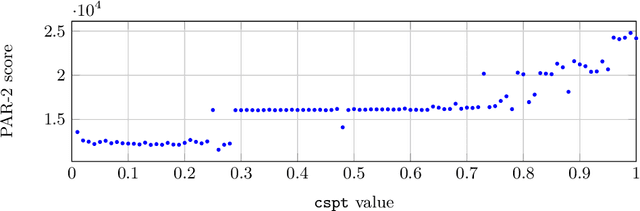
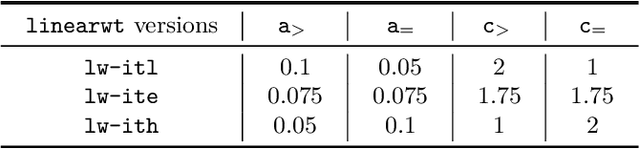
The Divide and Distribute Fixed Weights algorithm (ddfw) is a dynamic local search SAT-solving algorithm that transfers weight from satisfied to falsified clauses in local minima. ddfw is remarkably effective on several hard combinatorial instances. Yet, despite its success, it has received little study since its debut in 2005. In this paper, we propose three modifications to the base algorithm: a linear weight transfer method that moves a dynamic amount of weight between clauses in local minima, an adjustment to how satisfied clauses are chosen in local minima to give weight, and a weighted-random method of selecting variables to flip. We implemented our modifications to ddfw on top of the solver yalsat. Our experiments show that our modifications boost the performance compared to the original ddfw algorithm on multiple benchmarks, including those from the past three years of SAT competitions. Moreover, our improved solver exclusively solves hard combinatorial instances that refute a conjecture on the lower bound of two Van der Waerden numbers set forth by Ahmed et al. (2014), and it performs well on a hard graph-coloring instance that has been open for over three decades.

A Deep Dive into Conflict Generating Decisions

Boolean Satisfiability (SAT) is a well-known NP-complete problem. Despite this theoretical hardness, SAT solvers based on Conflict Driven Clause Learning (CDCL) can solve large SAT instances from many important domains. CDCL learns clauses from conflicts, a technique that allows a solver to prune its search space. The selection heuristics in CDCL prioritize variables that are involved in recent conflicts. While only a fraction of decisions generate any conflicts, many generate multiple conflicts. In this paper, we study conflict-generating decisions in CDCL in detail. We investigate the impact of single conflict (sc) decisions, which generate only one conflict, and multi-conflict (mc) decisions which generate two or more. We empirically characterize these two types of decisions based on the quality of the learned clauses produced by each type of decision. We also show an important connection between consecutive clauses learned within the same mc decision, where one learned clause triggers the learning of the next one forming a chain of clauses. This leads to the consideration of similarity between conflicts, for which we formulate the notion of conflictsproximity as a similarity measure. We show that conflicts in mc decisions are more closely related than consecutive conflicts generated from sc decisions. Finally, we develop Common Reason Variable Reduction (CRVR) as a new decision strategy that reduces the selection priority of some variables from the learned clauses of mc decisions. Our empirical evaluation of CRVR implemented in three leading solvers demonstrates performance gains in benchmarks from the main track of SAT Competition-2020.

Characterization of Glue Variables in CDCL SAT Solving

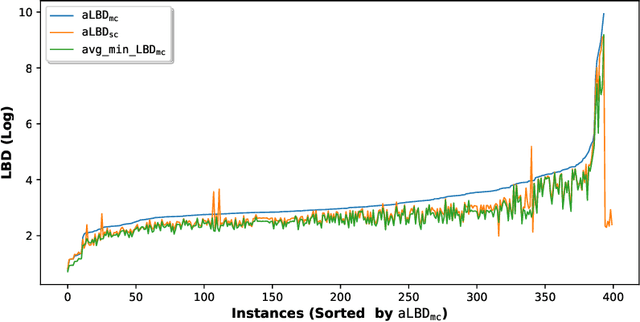
A state-of-the-art criterion to evaluate the importance of a given learned clause is called Literal Block Distance (LBD) score. It measures the number of distinct decision levels in a given learned clause. The lower the LBD score of a learned clause, the better is its quality. The learned clauses with LBD score of 2, called glue clauses, are known to possess high pruning power which are never deleted from the clause databases of the modern CDCL SAT solvers. In this work, we relate glue clauses to decision variables. We call the variables that appeared in at least one glue clause up to the current search state Glue Variables. We first show experimentally, by running the state-of-the-art CDCL SAT solver MapleLCMDist on benchmarks from SAT Competition-2017 and 2018, that branching decisions with glue variables are categorically more inference and conflict efficient than nonglue variables. Based on this observation, we develop a structure aware CDCL variable bumping scheme, which bumps the activity score of a glue variable based on its appearance count in the glue clauses that are learned so far by the search. Empirical evaluation shows effectiveness of the new method over the main track instances from SAT Competition 2017 and 2018.

Evolving Real-Time Heuristics Search Algorithms with Building Blocks

The research area of real-time heuristics search has produced quite many algorithms. In the landscape of real-time heuristics search research, it is not rare to find that an algorithm X that appears to perform better than algorithm Y on a group of problems, performed worse than Y for another group of problems. If these published algorithms are combined to generate a more powerful space of algorithms, then that novel space of algorithms may solve a distribution of problems more efficiently. Based on this intuition, a recent work Bulitko 2016 has defined the task of finding a combination of heuristics search algorithms as a survival task. In this evolutionary approach, a space of algorithms is defined over a set of building blocks published algorithms and a simulated evolution is used to recombine these building blocks to find out the best algorithm from that space of algorithms. In this paper, we extend the set of building blocks by adding one published algorithm, namely lookahead based A-star shaped local search space generation method from LSSLRTA-star, plus an unpublished novel strategy to generate local search space with Greedy Best First Search. Then we perform experiments in the new space of algorithms, which show that the best algorithms selected by the evolutionary process have the following property: the deeper is the lookahead depth of an algorithm, the lower is its suboptimality and scrubbing complexity.