On the Foundations of Conflict-Driven Solving for Hybrid MKNF Knowledge Bases

Hybrid MKNF Knowledge Bases (HMKNF-KBs) constitute a formalism for tightly integrated reasoning over closed-world rules and open-world ontologies. This approach allows for accurate modeling of real-world systems, which often rely on both categorical and normative reasoning. Conflict-driven solving is the leading approach for computationally hard problems, such as satisfiability (SAT) and answer set programming (ASP), in which MKNF is rooted. This paper investigates the theoretical underpinnings required for a conflict-driven solver of HMKNF-KBs. The approach defines a set of completion and loop formulas, whose satisfaction characterizes MKNF models. This forms the basis for a set of nogoods, which in turn can be used as the backbone for a conflict-driven solver.

Eliminating Unintended Stable Fixpoints for Hybrid Reasoning Systems

A wide variety of nonmonotonic semantics can be expressed as approximators defined under AFT (Approximation Fixpoint Theory). Using traditional AFT theory, it is not possible to define approximators that rely on information computed in previous iterations of stable revision. However, this information is rich for semantics that incorporate classical negation into nonmonotonic reasoning. In this work, we introduce a methodology resembling AFT that can utilize priorly computed upper bounds to more precisely capture semantics. We demonstrate our framework's applicability to hybrid MKNF (minimal knowledge and negation as failure) knowledge bases by extending the state-of-the-art approximator.

A Fixpoint Characterization of Three-Valued Disjunctive Hybrid MKNF Knowledge Bases

The logic of hybrid MKNF (minimal knowledge and negation as failure) is a powerful knowledge representation language that elegantly pairs ASP (answer set programming) with ontologies. Disjunctive rules are a desirable extension to normal rule-based reasoning and typically semantic frameworks designed for normal knowledge bases need substantial restructuring to support disjunctive rules. Alternatively, one may lift characterizations of normal rules to support disjunctive rules by inducing a collection of normal knowledge bases, each with the same body and a single atom in its head. In this work, we refer to a set of such normal knowledge bases as a head-cut of a disjunctive knowledge base. The question arises as to whether the semantics of disjunctive hybrid MKNF knowledge bases can be characterized using fixpoint constructions with head-cuts. Earlier, we have shown that head-cuts can be paired with fixpoint operators to capture the two-valued MKNF models of disjunctive hybrid MKNF knowledge bases. Three-valued semantics extends two-valued semantics with the ability to express partial information. In this work, we present a fixpoint construction that leverages head-cuts using an operator that iteratively captures three-valued models of hybrid MKNF knowledge bases with disjunctive rules. This characterization also captures partial stable models of disjunctive logic programs since a program can be expressed as a disjunctive hybrid MKNF knowledge base with an empty ontology. We elaborate on a relationship between this characterization and approximators in AFT (approximation fixpoint theory) for normal hybrid MKNF knowledge bases.

Towards Universal Languages for Tractable Ontology Mediated Query Answering

An ontology language for ontology mediated query answering (OMQA-language) is universal for a family of OMQA-languages if it is the most expressive one among this family. In this paper, we focus on three families of tractable OMQA-languages, including first-order rewritable languages and languages whose data complexity of the query answering is in AC0 or PTIME. On the negative side, we prove that there is, in general, no universal language for each of these families of languages. On the positive side, we propose a novel property, the locality, to approximate the first-order rewritability, and show that there exists a language of disjunctive embedded dependencies that is universal for the family of OMQA-languages with locality. All of these results apply to OMQA with query languages such as conjunctive queries, unions of conjunctive queries and acyclic conjunctive queries.

Mutex Graphs and Multicliques: Reducing Grounding Size for Planning

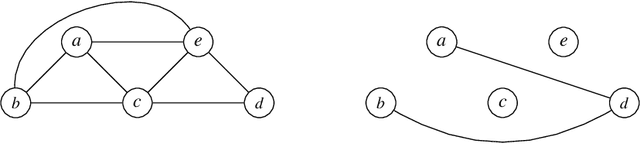
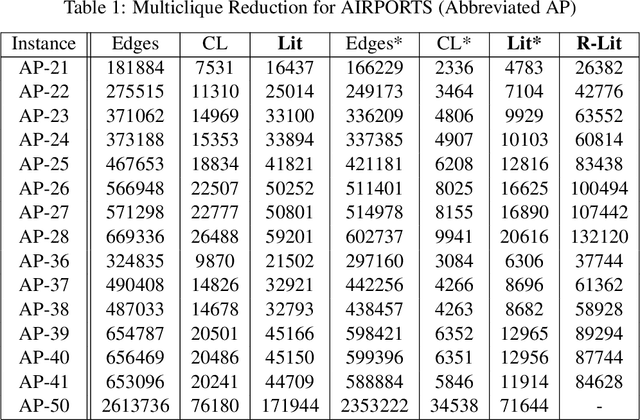
We present an approach to representing large sets of mutual exclusions, also known as mutexes or mutex constraints. These are the types of constraints that specify the exclusion of some properties, events, processes, and so on. They are ubiquitous in many areas of applications. The size of these constraints for a given problem can be overwhelming enough to present a bottleneck for the solving efficiency of the underlying solver. In this paper, we propose a novel graph-theoretic technique based on multicliques for a compact representation of mutex constraints and apply it to domain-independent planning in ASP. As computing a minimum multiclique covering from a mutex graph is NP-hard, we propose an efficient approximation algorithm for multiclique covering and show experimentally that it generates substantially smaller grounding size for mutex constraints in ASP than the previously known work in SAT.

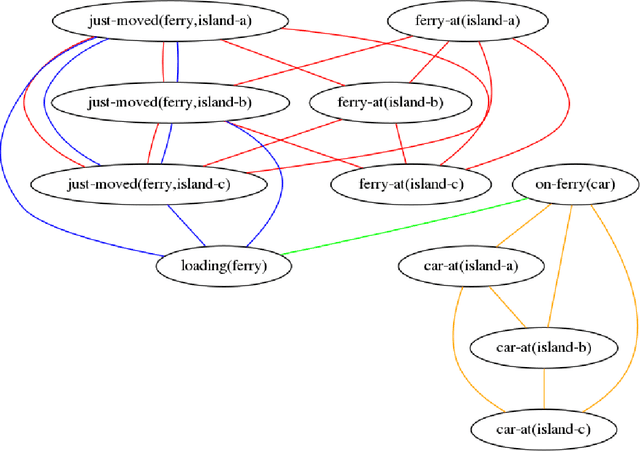
Domain-Independent Cost-Optimal Planning in ASP

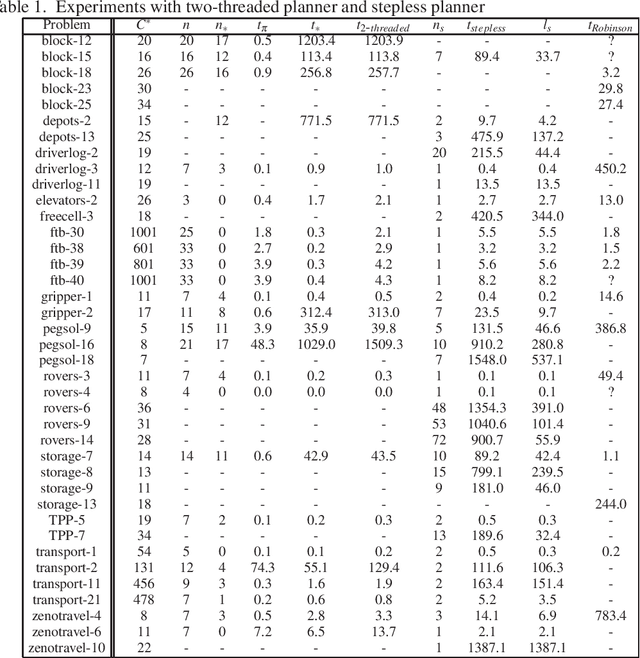
We investigate the problem of cost-optimal planning in ASP. Current ASP planners can be trivially extended to a cost-optimal one by adding weak constraints, but only for a given makespan (number of steps). It is desirable to have a planner that guarantees global optimality. In this paper, we present two approaches to addressing this problem. First, we show how to engineer a cost-optimal planner composed of two ASP programs running in parallel. Using lessons learned from this, we then develop an entirely new approach to cost-optimal planning, stepless planning, which is completely free of makespan. Experiments to compare the two approaches with the only known cost-optimal planner in SAT reveal good potentials for stepless planning in ASP. The paper is under consideration for acceptance in TPLP.

Characterization of Glue Variables in CDCL SAT Solving

A state-of-the-art criterion to evaluate the importance of a given learned clause is called Literal Block Distance (LBD) score. It measures the number of distinct decision levels in a given learned clause. The lower the LBD score of a learned clause, the better is its quality. The learned clauses with LBD score of 2, called glue clauses, are known to possess high pruning power which are never deleted from the clause databases of the modern CDCL SAT solvers. In this work, we relate glue clauses to decision variables. We call the variables that appeared in at least one glue clause up to the current search state Glue Variables. We first show experimentally, by running the state-of-the-art CDCL SAT solver MapleLCMDist on benchmarks from SAT Competition-2017 and 2018, that branching decisions with glue variables are categorically more inference and conflict efficient than nonglue variables. Based on this observation, we develop a structure aware CDCL variable bumping scheme, which bumps the activity score of a glue variable based on its appearance count in the glue clauses that are learned so far by the search. Empirical evaluation shows effectiveness of the new method over the main track instances from SAT Competition 2017 and 2018.

Well-Founded Operators for Normal Hybrid MKNF Knowledge Bases

Hybrid MKNF knowledge bases have been considered one of the dominant approaches to combining open world ontology languages with closed world rule-based languages. Currently, the only known inference methods are based on the approach of guess-and-verify, while most modern SAT/ASP solvers are built under the DPLL architecture. The central impediment here is that it is not clear what constitutes a constraint propagator, a key component employed in any DPLL-based solver. In this paper, we address this problem by formulating the notion of unfounded sets for nondisjunctive hybrid MKNF knowledge bases, based on which we propose and study two new well-founded operators. We show that by employing a well-founded operator as a constraint propagator, a sound and complete DPLL search engine can be readily defined. We compare our approach with the operator based on the alternating fixpoint construction by Knorr et al [2011] and show that, when applied to arbitrary partial partitions, the new well-founded operators not only propagate more truth values but also circumvent the non-converging behavior of the latter. In addition, we study the possibility of simplifying a given hybrid MKNF knowledge base by employing a well-founded operator, and show that, out of the two operators proposed in this paper, the weaker one can be applied for this purpose and the stronger one cannot. These observations are useful in implementing a grounder for hybrid MKNF knowledge bases, which can be applied before the computation of MKNF models. The paper is under consideration for acceptance in TPLP.

Expressive Completeness of Existential Rule Languages for Ontology-based Query Answering

Existential rules, also known as data dependencies in Databases, have been recently rediscovered as a promising family of languages for Ontology-based Query Answering. In this paper, we prove that disjunctive embedded dependencies exactly capture the class of recursively enumerable ontologies in Ontology-based Conjunctive Query Answering (OCQA). Our expressive completeness result does not rely on any built-in linear order on the database. To establish the expressive completeness, we introduce a novel semantic definition for OCQA ontologies. We also show that neither the class of disjunctive tuple-generating dependencies nor the class of embedded dependencies is expressively complete for recursively enumerable OCQA ontologies.

Existential Rule Languages with Finite Chase: Complexity and Expressiveness

Finite chase, or alternatively chase termination, is an important condition to ensure the decidability of existential rule languages. In the past few years, a number of rule languages with finite chase have been studied. In this work, we propose a novel approach for classifying the rule languages with finite chase. Using this approach, a family of decidable rule languages, which extend the existing languages with the finite chase property, are naturally defined. We then study the complexity of these languages. Although all of them are tractable for data complexity, we show that their combined complexity can be arbitrarily high. Furthermore, we prove that all the rule languages with finite chase that extend the weakly acyclic language are of the same expressiveness as the weakly acyclic one, while rule languages with higher combined complexity are in general more succinct than those with lower combined complexity.