Expected Work Search: Combining Win Rate and Proof Size Estimation

We propose Expected Work Search (EWS), a new game solving algorithm. EWS combines win rate estimation, as used in Monte Carlo Tree Search, with proof size estimation, as used in Proof Number Search. The search efficiency of EWS stems from minimizing a novel notion of Expected Work, which predicts the expected computation required to solve a position. EWS outperforms traditional solving algorithms on the games of Go and Hex. For Go, we present the first solution to the empty 5x5 board with the commonly used positional superko ruleset. For Hex, our algorithm solves the empty 8x8 board in under 4 minutes. Experiments show that EWS succeeds both with and without extensive domain-specific knowledge.

Mutex Graphs and Multicliques: Reducing Grounding Size for Planning

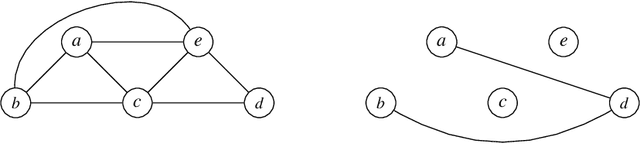
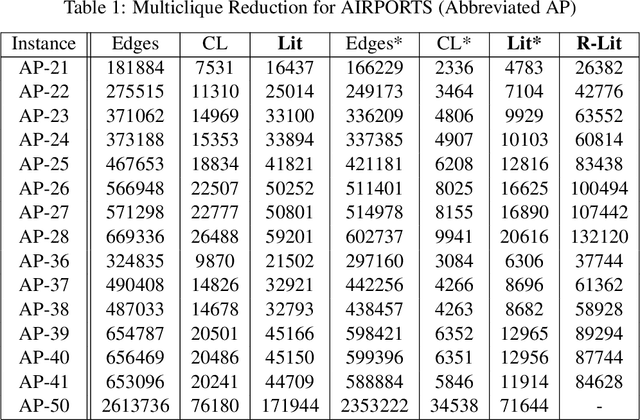
We present an approach to representing large sets of mutual exclusions, also known as mutexes or mutex constraints. These are the types of constraints that specify the exclusion of some properties, events, processes, and so on. They are ubiquitous in many areas of applications. The size of these constraints for a given problem can be overwhelming enough to present a bottleneck for the solving efficiency of the underlying solver. In this paper, we propose a novel graph-theoretic technique based on multicliques for a compact representation of mutex constraints and apply it to domain-independent planning in ASP. As computing a minimum multiclique covering from a mutex graph is NP-hard, we propose an efficient approximation algorithm for multiclique covering and show experimentally that it generates substantially smaller grounding size for mutex constraints in ASP than the previously known work in SAT.

Domain-Independent Cost-Optimal Planning in ASP

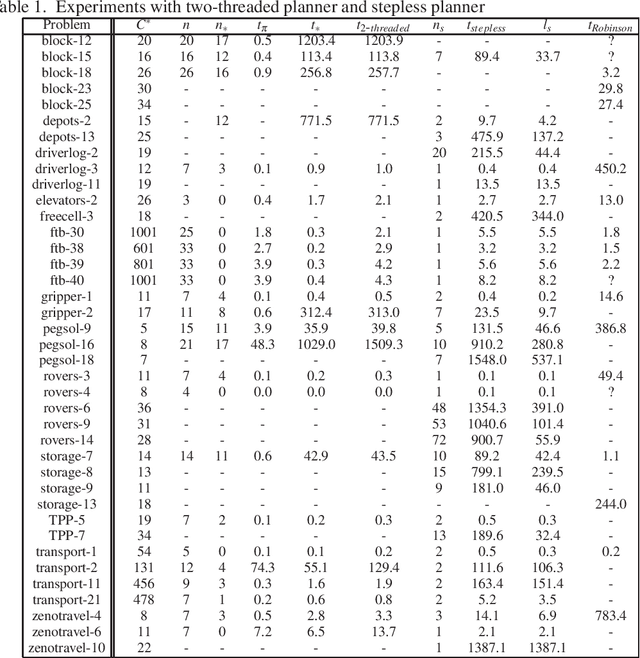
We investigate the problem of cost-optimal planning in ASP. Current ASP planners can be trivially extended to a cost-optimal one by adding weak constraints, but only for a given makespan (number of steps). It is desirable to have a planner that guarantees global optimality. In this paper, we present two approaches to addressing this problem. First, we show how to engineer a cost-optimal planner composed of two ASP programs running in parallel. Using lessons learned from this, we then develop an entirely new approach to cost-optimal planning, stepless planning, which is completely free of makespan. Experiments to compare the two approaches with the only known cost-optimal planner in SAT reveal good potentials for stepless planning in ASP. The paper is under consideration for acceptance in TPLP.

Neurohex: A Deep Q-learning Hex Agent

DeepMind's recent spectacular success in using deep convolutional neural nets and machine learning to build superhuman level agents --- e.g. for Atari games via deep Q-learning and for the game of Go via Reinforcement Learning --- raises many questions, including to what extent these methods will succeed in other domains. In this paper we consider DQL for the game of Hex: after supervised initialization, we use selfplay to train NeuroHex, an 11-layer CNN that plays Hex on the 13x13 board. Hex is the classic two-player alternate-turn stone placement game played on a rhombus of hexagonal cells in which the winner is whomever connects their two opposing sides. Despite the large action and state space, our system trains a Q-network capable of strong play with no search. After two weeks of Q-learning, NeuroHex achieves win-rates of 20.4% as first player and 2.1% as second player against a 1-second/move version of MoHex, the current ICGA Olympiad Hex champion. Our data suggests further improvement might be possible with more training time.