Solving 7x7 Killall-Go with Seki Database

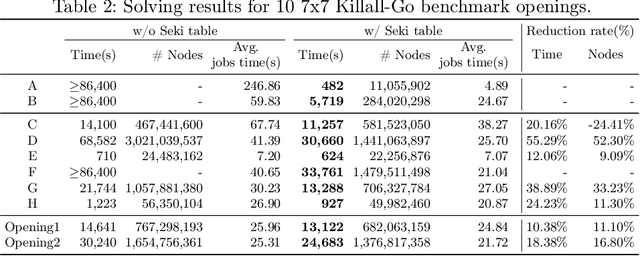
Game solving is the process of finding the theoretical outcome for a game, assuming that all player choices are optimal. This paper focuses on a technique that can reduce the heuristic search space significantly for 7x7 Killall-Go. In Go and Killall-Go, live patterns are stones that are protected from opponent capture. Mutual life, also referred to as seki, is when both players' stones achieve life by sharing liberties with their opponent. Whichever player attempts to capture the opponent first will leave their own stones vulnerable. Therefore, it is critical to recognize seki patterns to avoid putting oneself in jeopardy. Recognizing seki can reduce the search depth significantly. In this paper, we enumerate all seki patterns up to a predetermined area size, then store these patterns into a seki table. This allows us to recognize seki during search, which significantly improves solving efficiency for the game of Killall-Go. Experiments show that a day-long, unsolvable position can be solved in 482 seconds with the addition of a seki table. For general positions, a 10% to 20% improvement in wall clock time and node count is observed.

Expected Work Search: Combining Win Rate and Proof Size Estimation

We propose Expected Work Search (EWS), a new game solving algorithm. EWS combines win rate estimation, as used in Monte Carlo Tree Search, with proof size estimation, as used in Proof Number Search. The search efficiency of EWS stems from minimizing a novel notion of Expected Work, which predicts the expected computation required to solve a position. EWS outperforms traditional solving algorithms on the games of Go and Hex. For Go, we present the first solution to the empty 5x5 board with the commonly used positional superko ruleset. For Hex, our algorithm solves the empty 8x8 board in under 4 minutes. Experiments show that EWS succeeds both with and without extensive domain-specific knowledge.

Game Solving with Online Fine-Tuning

Game solving is a similar, yet more difficult task than mastering a game. Solving a game typically means to find the game-theoretic value (outcome given optimal play), and optionally a full strategy to follow in order to achieve that outcome. The AlphaZero algorithm has demonstrated super-human level play, and its powerful policy and value predictions have also served as heuristics in game solving. However, to solve a game and obtain a full strategy, a winning response must be found for all possible moves by the losing player. This includes very poor lines of play from the losing side, for which the AlphaZero self-play process will not encounter. AlphaZero-based heuristics can be highly inaccurate when evaluating these out-of-distribution positions, which occur throughout the entire search. To address this issue, this paper investigates applying online fine-tuning while searching and proposes two methods to learn tailor-designed heuristics for game solving. Our experiments show that using online fine-tuning can solve a series of challenging 7x7 Killall-Go problems, using only 23.54% of computation time compared to the baseline without online fine-tuning. Results suggest that the savings scale with problem size. Our method can further be extended to any tree search algorithm for problem solving. Our code is available at https://rlg.iis.sinica.edu.tw/papers/neurips2023-online-fine-tuning-solver.

MiniZero: Comparative Analysis of AlphaZero and MuZero on Go, Othello, and Atari Games

This paper presents MiniZero, a zero-knowledge learning framework that supports four state-of-the-art algorithms, including AlphaZero, MuZero, Gumbel AlphaZero, and Gumbel MuZero. While these algorithms have demonstrated super-human performance in many games, it remains unclear which among them is most suitable or efficient for specific tasks. Through MiniZero, we systematically evaluate the performance of each algorithm in two board games, 9x9 Go and 8x8 Othello, as well as 57 Atari games. Our empirical findings are summarized as follows. For two board games, using more simulations generally results in higher performance. However, the choice of AlphaZero and MuZero may differ based on game properties. For Atari games, both MuZero and Gumbel MuZero are worth considering. Since each game has unique characteristics, different algorithms and simulations yield varying results. In addition, we introduce an approach, called progressive simulation, which progressively increases the simulation budget during training to allocate computation more efficiently. Our empirical results demonstrate that progressive simulation achieves significantly superior performance in two board games. By making our framework and trained models publicly available, this paper contributes a benchmark for future research on zero-knowledge learning algorithms, assisting researchers in algorithm selection and comparison against these zero-knowledge learning baselines.

A Local-Pattern Related Look-Up Table

This paper describes a Relevance-Zone pattern table (RZT) that can be used to replace a traditional transposition table. An RZT stores exact game values for patterns that are discovered during a Relevance-Zone-Based Search (RZS), which is the current state-of-the-art in solving L&D problems in Go. Positions that share the same pattern can reuse the same exact game value in the RZT. The pattern matching scheme for RZTs is implemented using a radix tree, taking into consideration patterns with different shapes. To improve the efficiency of table lookups, we designed a heuristic that prevents redundant lookups. The heuristic can safely skip previously queried patterns for a given position, reducing the overhead to 10% of the original cost. We also analyze the time complexity of the RZT both theoretically and empirically. Experiments show the overhead of traversing the radix tree in practice during lookup remain flat logarithmically in relation to the number of entries stored in the table. Experiments also show that the use of an RZT instead of a traditional transposition table significantly reduces the number of searched nodes on two data sets of 7x7 and 19x19 L&D Go problems.

A Novel Approach to Solving Goal-Achieving Problems for Board Games

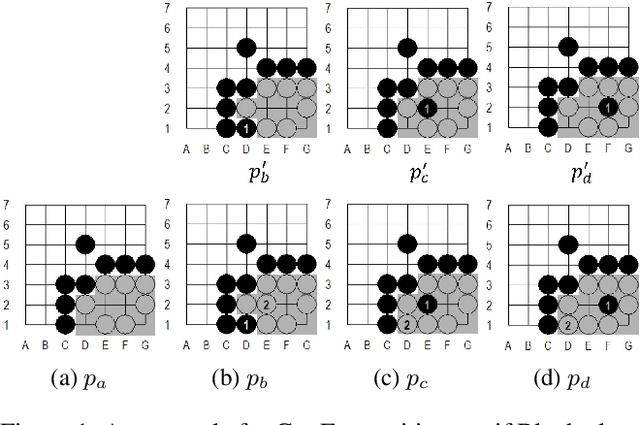
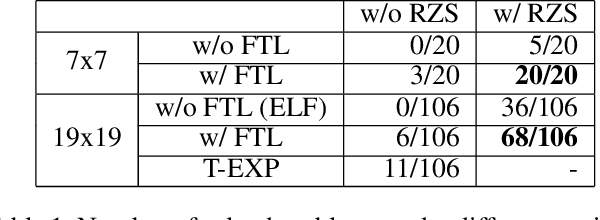
Goal-achieving problems are puzzles that set up a specific situation with a clear objective. An example that is well-studied is the category of life-and-death (L&D) problems for Go, which helps players hone their skill of identifying region safety. Many previous methods like lambda search try null moves first, then derive so-called relevance zones (RZs), outside of which the opponent does not need to search. This paper first proposes a novel RZ-based approach, called the RZ-Based Search (RZS), to solving L&D problems for Go. RZS tries moves before determining whether they are null moves post-hoc. This means we do not need to rely on null move heuristics, resulting in a more elegant algorithm, so that it can also be seamlessly incorporated into AlphaZero's super-human level play in our solver. To repurpose AlphaZero for solving, we also propose a new training method called Faster to Life (FTL), which modifies AlphaZero to entice it to win more quickly. We use RZS and FTL to solve L&D problems on Go, namely solving 68 among 106 problems from a professional L&D book while a previous program solves 11 only. Finally, we discuss that the approach is generic in the sense that RZS is applicable to solving many other goal-achieving problems for board games.

Towards Combining On-Off-Policy Methods for Real-World Applications

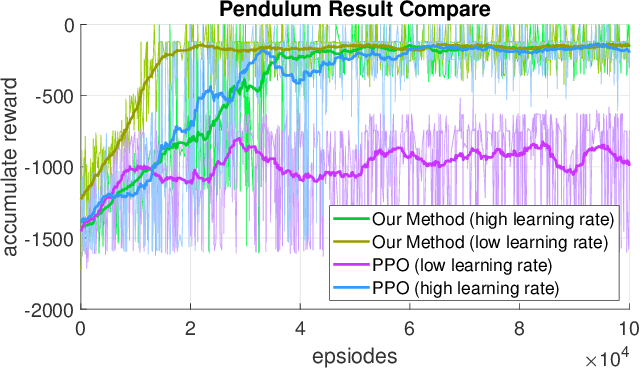
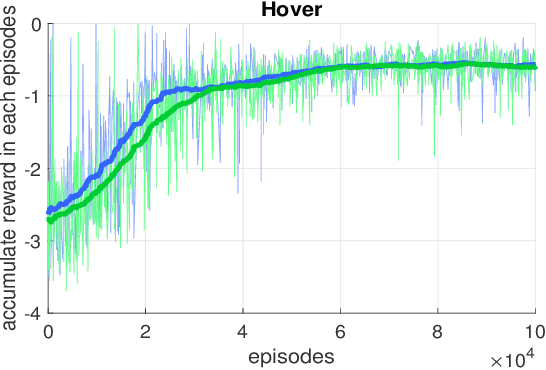
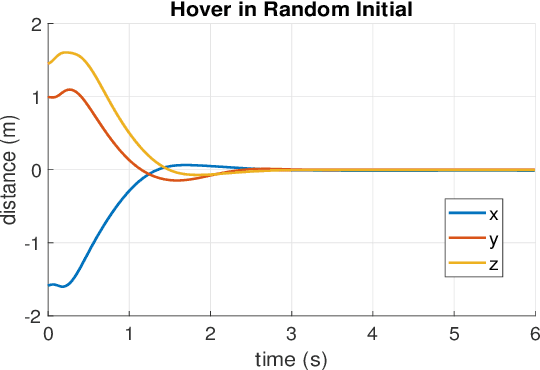
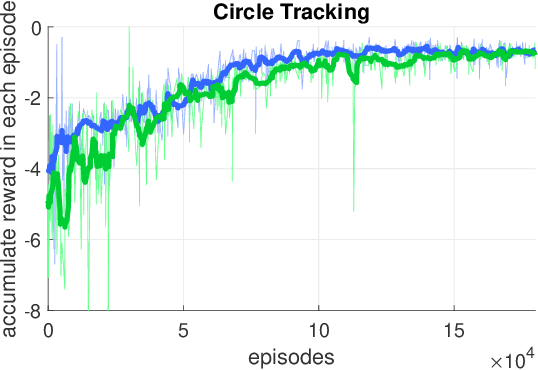
In this paper, we point out a fundamental property of the objective in reinforcement learning, with which we can reformulate the policy gradient objective into a perceptron-like loss function, removing the need to distinguish between on and off policy training. Namely, we posit that it is sufficient to only update a policy $\pi$ for cases that satisfy the condition $A(\frac{\pi}{\mu}-1)\leq0$, where $A$ is the advantage, and $\mu$ is another policy. Furthermore, we show via theoretic derivation that a perceptron-like loss function matches the clipped surrogate objective for PPO. With our new formulation, the policies $\pi$ and $\mu$ can be arbitrarily apart in theory, effectively enabling off-policy training. To examine our derivations, we can combine the on-policy PPO clipped surrogate (which we show to be equivalent with one instance of the new reformation) with the off-policy IMPALA method. We first verify the combined method on the OpenAI Gym pendulum toy problem. Next, we use our method to train a quadrotor position controller in a simulator. Our trained policy is efficient and lightweight enough to perform in a low cost micro-controller at a minimum update rate of 500 Hz. For the quadrotor, we show two experiments to verify our method and demonstrate performance: 1) hovering at a fixed position, and 2) tracking along a specific trajectory. In preliminary trials, we are also able to apply the method to a real-world quadrotor.