MAPLE: Multi-State Aggregated Policy Evaluation for AlphaZero in Imperfect-Information Games

Imperfect-information games (IIGs) are challenging, as players must make decisions without fully observing the true game state. While AlphaZero has achieved remarkable success in perfect-information games, extending it to IIGs remains difficult. Existing search-based approaches, such as Perfect Information Monte Carlo (PIMC), suffer from strategy fusion, while Information Set Monte Carlo Tree Search (IS-MCTS) incurs high computational cost when combined with neural networks. In this paper, we propose Multi-State Aggregated PoLicy Evaluation (MAPLE), a tree search method that aggregates policy and value evaluations from multiple sampled world states within a single search tree, combining the advantages of PIMC and IS-MCTS while maintaining a controllable computational cost. We further incorporate a Siamese-based sampling strategy to select informative world states from the information set. Experiments on Phantom Go and Dark Hex show that MAPLE significantly outperforms the PIMC-based AlphaZero baseline, achieving Elo improvements of 291 and 136, respectively. These results demonstrate that MAPLE is an effective approach for AlphaZero-style learning in imperfect-information games.

Evaluating Game Difficulty in Tetris Block Puzzle

Tetris Block Puzzle is a single player stochastic puzzle in which a player places blocks on an 8 x 8 grid to complete lines; its popular variants have amassed tens of millions of downloads. Despite this reach, there is little principled assessment of which rule sets are more difficult. Inspired by prior work that uses AlphaZero as a strong evaluator for chess variants, we study difficulty in this domain using Stochastic Gumbel AlphaZero (SGAZ), a budget-aware planning agent for stochastic environments. We evaluate rule changes including holding block h, preview holding block p, and additional Tetris block variants using metrics such as training reward and convergence iterations. Empirically, increasing h and p reduces difficulty (higher reward and faster convergence), while adding more Tetris block variants increases difficulty, with the T-pentomino producing the largest slowdown. Through analysis, SGAZ delivers strong play under small simulation budgets, enabling efficient, reproducible comparisons across rule sets and providing a reference for future design in stochastic puzzle games.

A Study of Solving Life-and-Death Problems in Go Using Relevance-Zone Based Solvers

This paper analyzes the behavior of solving Life-and-Death (L&D) problems in the game of Go using current state-of-the-art computer Go solvers with two techniques: the Relevance-Zone Based Search (RZS) and the relevance-zone pattern table. We examined the solutions derived by relevance-zone based solvers on seven L&D problems from the renowned book "Life and Death Dictionary" written by Cho Chikun, a Go grandmaster, and found several interesting results. First, for each problem, the solvers identify a relevance-zone that highlights the critical areas for solving. Second, the solvers discover a series of patterns, including some that are rare. Finally, the solvers even find different answers compared to the given solutions for two problems. We also identified two issues with the solver: (a) it misjudges values of rare patterns, and (b) it tends to prioritize living directly rather than maximizing territory, which differs from the behavior of human Go players. We suggest possible approaches to address these issues in future work. Our code and data are available at https://rlg.iis.sinica.edu.tw/papers/study-LD-RZ.

Relevance-Zone Reduction in Game Solving

Game solving aims to find the optimal strategies for all players and determine the theoretical outcome of a game. However, due to the exponential growth of game trees, many games remain unsolved, even though methods like AlphaZero have demonstrated super-human level in game playing. The Relevance-Zone (RZ) is a local strategy reuse technique that restricts the search to only the regions relevant to the outcome, significantly reducing the search space. However, RZs are not unique. Different solutions may result in RZs of varying sizes. Smaller RZs are generally more favorable, as they increase the chance of reuse and improve pruning efficiency. To this end, we propose an iterative RZ reduction method that repeatedly solves the same position while gradually restricting the region involved, guiding the solver toward smaller RZs. We design three constraint generation strategies and integrate an RZ Pattern Table to fully leverage past solutions. In experiments on 7x7 Killall-Go, our method reduces the average RZ size to 85.95% of the original. Furthermore, the reduced RZs can be permanently stored as reusable knowledge for future solving tasks, especially for larger board sizes or different openings.

OptionZero: Planning with Learned Options

Planning with options -- a sequence of primitive actions -- has been shown effective in reinforcement learning within complex environments. Previous studies have focused on planning with predefined options or learned options through expert demonstration data. Inspired by MuZero, which learns superhuman heuristics without any human knowledge, we propose a novel approach, named OptionZero. OptionZero incorporates an option network into MuZero, providing autonomous discovery of options through self-play games. Furthermore, we modify the dynamics network to provide environment transitions when using options, allowing searching deeper under the same simulation constraints. Empirical experiments conducted in 26 Atari games demonstrate that OptionZero outperforms MuZero, achieving a 131.58% improvement in mean human-normalized score. Our behavior analysis shows that OptionZero not only learns options but also acquires strategic skills tailored to different game characteristics. Our findings show promising directions for discovering and using options in planning. Our code is available at https://rlg.iis.sinica.edu.tw/papers/optionzero.

Solving 7x7 Killall-Go with Seki Database

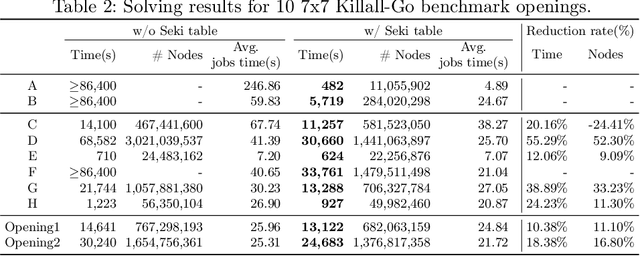
Game solving is the process of finding the theoretical outcome for a game, assuming that all player choices are optimal. This paper focuses on a technique that can reduce the heuristic search space significantly for 7x7 Killall-Go. In Go and Killall-Go, live patterns are stones that are protected from opponent capture. Mutual life, also referred to as seki, is when both players' stones achieve life by sharing liberties with their opponent. Whichever player attempts to capture the opponent first will leave their own stones vulnerable. Therefore, it is critical to recognize seki patterns to avoid putting oneself in jeopardy. Recognizing seki can reduce the search depth significantly. In this paper, we enumerate all seki patterns up to a predetermined area size, then store these patterns into a seki table. This allows us to recognize seki during search, which significantly improves solving efficiency for the game of Killall-Go. Experiments show that a day-long, unsolvable position can be solved in 482 seconds with the addition of a seki table. For general positions, a 10% to 20% improvement in wall clock time and node count is observed.

Interpreting the Learned Model in MuZero Planning

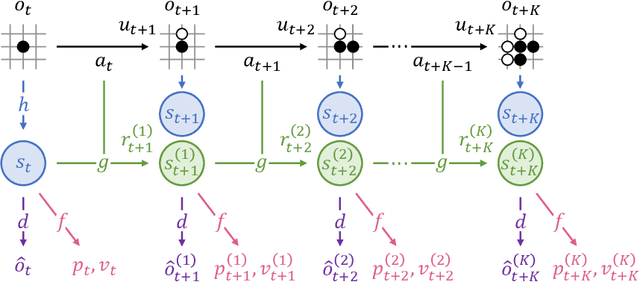
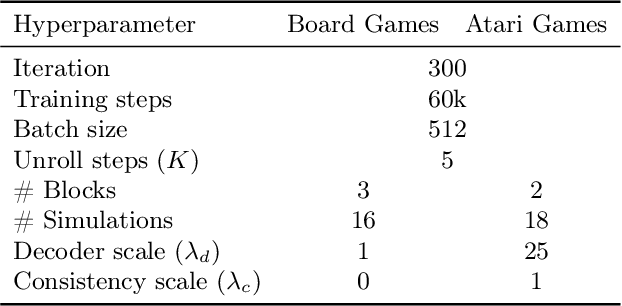
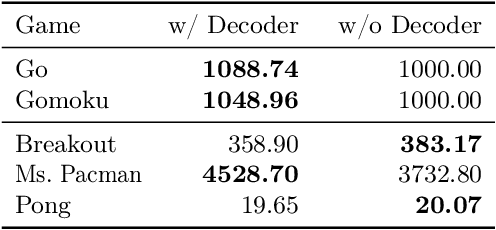
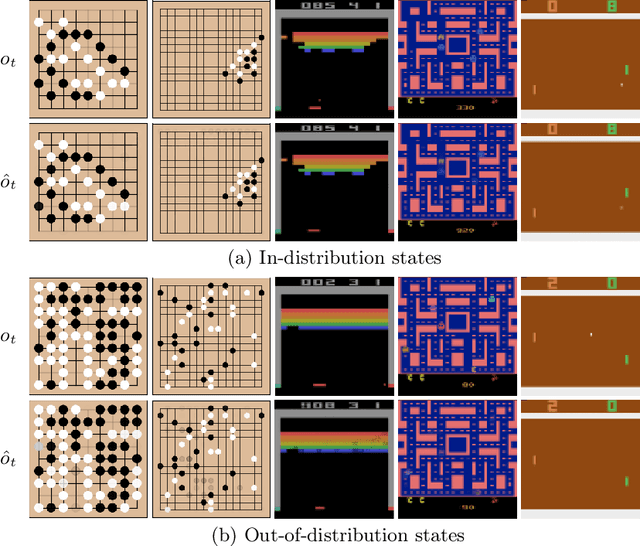
MuZero has achieved superhuman performance in various games by using a dynamics network to predict environment dynamics for planning, without relying on simulators. However, the latent states learned by the dynamics network make its planning process opaque. This paper aims to demystify MuZero's model by interpreting the learned latent states. We incorporate observation reconstruction and state consistency into MuZero training and conduct an in-depth analysis to evaluate latent states across two board games: 9x9 Go and Outer-Open Gomoku, and three Atari games: Breakout, Ms. Pacman, and Pong. Our findings reveal that while the dynamics network becomes less accurate over longer simulations, MuZero still performs effectively by using planning to correct errors. Our experiments also show that the dynamics network learns better latent states in board games than in Atari games. These insights contribute to a better understanding of MuZero and offer directions for future research to improve the playing performance, robustness, and interpretability of the MuZero algorithm.

Game Solving with Online Fine-Tuning

Game solving is a similar, yet more difficult task than mastering a game. Solving a game typically means to find the game-theoretic value (outcome given optimal play), and optionally a full strategy to follow in order to achieve that outcome. The AlphaZero algorithm has demonstrated super-human level play, and its powerful policy and value predictions have also served as heuristics in game solving. However, to solve a game and obtain a full strategy, a winning response must be found for all possible moves by the losing player. This includes very poor lines of play from the losing side, for which the AlphaZero self-play process will not encounter. AlphaZero-based heuristics can be highly inaccurate when evaluating these out-of-distribution positions, which occur throughout the entire search. To address this issue, this paper investigates applying online fine-tuning while searching and proposes two methods to learn tailor-designed heuristics for game solving. Our experiments show that using online fine-tuning can solve a series of challenging 7x7 Killall-Go problems, using only 23.54% of computation time compared to the baseline without online fine-tuning. Results suggest that the savings scale with problem size. Our method can further be extended to any tree search algorithm for problem solving. Our code is available at https://rlg.iis.sinica.edu.tw/papers/neurips2023-online-fine-tuning-solver.

MiniZero: Comparative Analysis of AlphaZero and MuZero on Go, Othello, and Atari Games

This paper presents MiniZero, a zero-knowledge learning framework that supports four state-of-the-art algorithms, including AlphaZero, MuZero, Gumbel AlphaZero, and Gumbel MuZero. While these algorithms have demonstrated super-human performance in many games, it remains unclear which among them is most suitable or efficient for specific tasks. Through MiniZero, we systematically evaluate the performance of each algorithm in two board games, 9x9 Go and 8x8 Othello, as well as 57 Atari games. Our empirical findings are summarized as follows. For two board games, using more simulations generally results in higher performance. However, the choice of AlphaZero and MuZero may differ based on game properties. For Atari games, both MuZero and Gumbel MuZero are worth considering. Since each game has unique characteristics, different algorithms and simulations yield varying results. In addition, we introduce an approach, called progressive simulation, which progressively increases the simulation budget during training to allocate computation more efficiently. Our empirical results demonstrate that progressive simulation achieves significantly superior performance in two board games. By making our framework and trained models publicly available, this paper contributes a benchmark for future research on zero-knowledge learning algorithms, assisting researchers in algorithm selection and comparison against these zero-knowledge learning baselines.

On Reinforcement Learning for the Game of 2048

2048 is a single-player stochastic puzzle game. This intriguing and addictive game has been popular worldwide and has attracted researchers to develop game-playing programs. Due to its simplicity and complexity, 2048 has become an interesting and challenging platform for evaluating the effectiveness of machine learning methods. This dissertation conducts comprehensive research on reinforcement learning and computer game algorithms for 2048. First, this dissertation proposes optimistic temporal difference learning, which significantly improves the quality of learning by employing optimistic initialization to encourage exploration for 2048. Furthermore, based on this approach, a state-of-the-art program for 2048 is developed, which achieves the highest performance among all learning-based programs, namely an average score of 625377 points and a rate of 72% for reaching 32768-tiles. Second, this dissertation investigates several techniques related to 2048, including the n-tuple network ensemble learning, Monte Carlo tree search, and deep reinforcement learning. These techniques are promising for further improving the performance of the current state-of-the-art program. Finally, this dissertation discusses pedagogical applications related to 2048 by proposing course designs and summarizing the teaching experience. The proposed course designs adopt 2048-like games as materials for beginners to learn reinforcement learning and computer game algorithms. The courses have been successfully applied to graduate-level students and received well by student feedback.