Relevance-Zone Reduction in Game Solving

Game solving aims to find the optimal strategies for all players and determine the theoretical outcome of a game. However, due to the exponential growth of game trees, many games remain unsolved, even though methods like AlphaZero have demonstrated super-human level in game playing. The Relevance-Zone (RZ) is a local strategy reuse technique that restricts the search to only the regions relevant to the outcome, significantly reducing the search space. However, RZs are not unique. Different solutions may result in RZs of varying sizes. Smaller RZs are generally more favorable, as they increase the chance of reuse and improve pruning efficiency. To this end, we propose an iterative RZ reduction method that repeatedly solves the same position while gradually restricting the region involved, guiding the solver toward smaller RZs. We design three constraint generation strategies and integrate an RZ Pattern Table to fully leverage past solutions. In experiments on 7x7 Killall-Go, our method reduces the average RZ size to 85.95% of the original. Furthermore, the reduced RZs can be permanently stored as reusable knowledge for future solving tasks, especially for larger board sizes or different openings.

Solving 7x7 Killall-Go with Seki Database

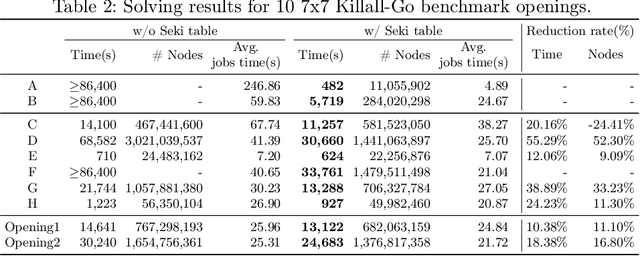
Game solving is the process of finding the theoretical outcome for a game, assuming that all player choices are optimal. This paper focuses on a technique that can reduce the heuristic search space significantly for 7x7 Killall-Go. In Go and Killall-Go, live patterns are stones that are protected from opponent capture. Mutual life, also referred to as seki, is when both players' stones achieve life by sharing liberties with their opponent. Whichever player attempts to capture the opponent first will leave their own stones vulnerable. Therefore, it is critical to recognize seki patterns to avoid putting oneself in jeopardy. Recognizing seki can reduce the search depth significantly. In this paper, we enumerate all seki patterns up to a predetermined area size, then store these patterns into a seki table. This allows us to recognize seki during search, which significantly improves solving efficiency for the game of Killall-Go. Experiments show that a day-long, unsolvable position can be solved in 482 seconds with the addition of a seki table. For general positions, a 10% to 20% improvement in wall clock time and node count is observed.

MiniZero: Comparative Analysis of AlphaZero and MuZero on Go, Othello, and Atari Games

This paper presents MiniZero, a zero-knowledge learning framework that supports four state-of-the-art algorithms, including AlphaZero, MuZero, Gumbel AlphaZero, and Gumbel MuZero. While these algorithms have demonstrated super-human performance in many games, it remains unclear which among them is most suitable or efficient for specific tasks. Through MiniZero, we systematically evaluate the performance of each algorithm in two board games, 9x9 Go and 8x8 Othello, as well as 57 Atari games. Our empirical findings are summarized as follows. For two board games, using more simulations generally results in higher performance. However, the choice of AlphaZero and MuZero may differ based on game properties. For Atari games, both MuZero and Gumbel MuZero are worth considering. Since each game has unique characteristics, different algorithms and simulations yield varying results. In addition, we introduce an approach, called progressive simulation, which progressively increases the simulation budget during training to allocate computation more efficiently. Our empirical results demonstrate that progressive simulation achieves significantly superior performance in two board games. By making our framework and trained models publicly available, this paper contributes a benchmark for future research on zero-knowledge learning algorithms, assisting researchers in algorithm selection and comparison against these zero-knowledge learning baselines.