Expected Shapley-Like Scores of Boolean Functions: Complexity and Applications to Probabilistic Databases

Shapley values, originating in game theory and increasingly prominent in explainable AI, have been proposed to assess the contribution of facts in query answering over databases, along with other similar power indices such as Banzhaf values. In this work we adapt these Shapley-like scores to probabilistic settings, the objective being to compute their expected value. We show that the computations of expected Shapley values and of the expected values of Boolean functions are interreducible in polynomial time, thus obtaining the same tractability landscape. We investigate the specific tractable case where Boolean functions are represented as deterministic decomposable circuits, designing a polynomial-time algorithm for this setting. We present applications to probabilistic databases through database provenance, and an effective implementation of this algorithm within the ProvSQL system, which experimentally validates its feasibility over a standard benchmark.

On the Complexity of SHAP-Score-Based Explanations: Tractability via Knowledge Compilation and Non-Approximability Results

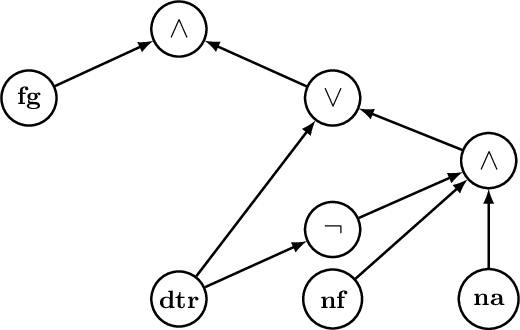
In Machine Learning, the $\mathsf{SHAP}$-score is a version of the Shapley value that is used to explain the result of a learned model on a specific entity by assigning a score to every feature. While in general computing Shapley values is an intractable problem, we prove a strong positive result stating that the $\mathsf{SHAP}$-score can be computed in polynomial time over deterministic and decomposable Boolean circuits. Such circuits are studied in the field of Knowledge Compilation and generalize a wide range of Boolean circuits and binary decision diagrams classes, including binary decision trees and Ordered Binary Decision Diagrams (OBDDs). We also establish the computational limits of the SHAP-score by observing that computing it over a class of Boolean models is always polynomially as hard as the model counting problem for that class. This implies that both determinism and decomposability are essential properties for the circuits that we consider. It also implies that computing $\mathsf{SHAP}$-scores is intractable as well over the class of propositional formulas in DNF. Based on this negative result, we look for the existence of fully-polynomial randomized approximation schemes (FPRAS) for computing $\mathsf{SHAP}$-scores over such class. In contrast to the model counting problem for DNF formulas, which admits an FPRAS, we prove that no such FPRAS exists for the computation of $\mathsf{SHAP}$-scores. Surprisingly, this negative result holds even for the class of monotone formulas in DNF. These techniques can be further extended to prove another strong negative result: Under widely believed complexity assumptions, there is no polynomial-time algorithm that checks, given a monotone DNF formula $\varphi$ and features $x,y$, whether the $\mathsf{SHAP}$-score of $x$ in $\varphi$ is smaller than the $\mathsf{SHAP}$-score of $y$ in $\varphi$.

Model Interpretability through the Lens of Computational Complexity

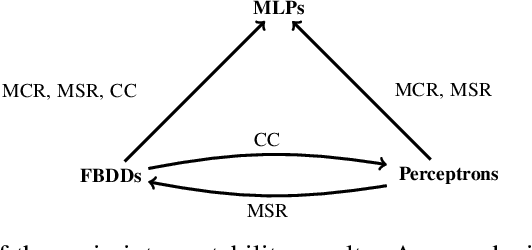
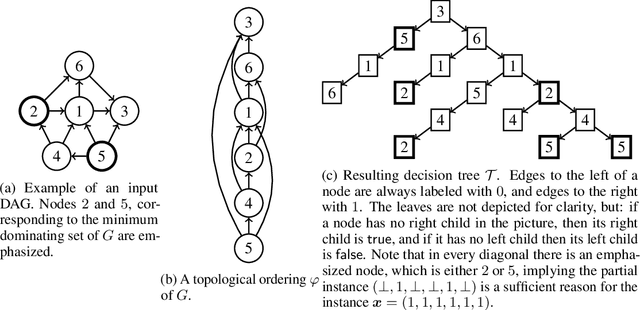
In spite of several claims stating that some models are more interpretable than others -- e.g., "linear models are more interpretable than deep neural networks" -- we still lack a principled notion of interpretability to formally compare among different classes of models. We make a step towards such a notion by studying whether folklore interpretability claims have a correlate in terms of computational complexity theory. We focus on local post-hoc explainability queries that, intuitively, attempt to answer why individual inputs are classified in a certain way by a given model. In a nutshell, we say that a class $\mathcal{C}_1$ of models is more interpretable than another class $\mathcal{C}_2$, if the computational complexity of answering post-hoc queries for models in $\mathcal{C}_2$ is higher than for those in $\mathcal{C}_1$. We prove that this notion provides a good theoretical counterpart to current beliefs on the interpretability of models; in particular, we show that under our definition and assuming standard complexity-theoretical assumptions (such as P$\neq$NP), both linear and tree-based models are strictly more interpretable than neural networks. Our complexity analysis, however, does not provide a clear-cut difference between linear and tree-based models, as we obtain different results depending on the particular post-hoc explanations considered. Finally, by applying a finer complexity analysis based on parameterized complexity, we are able to prove a theoretical result suggesting that shallow neural networks are more interpretable than deeper ones.

The Tractability of SHAP-scores over Deterministic and Decomposable Boolean Circuits

Scores based on Shapley values are currently widely used for providing explanations to classification results over machine learning models. A prime example of this corresponds to the influential SHAP-score, a version of the Shapley value in which the contribution of a set $S$ of features from a given entity $\mathbf{e}$ over a model $M$ is defined as the expected value in $M$ of the set of entities $\mathbf{e}'$ that coincide with $\mathbf{e}$ over all features in $S$. While in general computing Shapley values is a computationally intractable problem, it has recently been claimed that the SHAP-score can be computed in polynomial time over the class of decision trees. In this paper, we provide a proof of a stronger result over Boolean models: the SHAP-score can be computed in polynomial time over deterministic and decomposable Boolean circuits, also known as tractable probabilistic circuits. Such circuits encompass a wide range of Boolean circuits and binary decision diagrams classes, including binary decision trees and Ordered Binary Decision Diagrams (OBDDs). Moreover, we establish the computational limits of the notion of SHAP-score by showing that computing it over a class of Boolean models is always (polynomially) as hard as the model counting problem for this class (under some mild condition). This implies, for instance, that computing the SHAP-score for DNF propositional formulae is a #P-hard problem, and, thus, that determinism is essential for the circuits that we consider.