Mitigating Matching Biases Through Score Calibration

Record matching, the task of identifying records that correspond to the same real-world entities across databases, is critical for data integration in domains like healthcare, finance, and e-commerce. While traditional record matching models focus on optimizing accuracy, fairness issues, such as demographic disparities in model performance, have attracted increasing attention. Biased outcomes in record matching can result in unequal error rates across demographic groups, raising ethical and legal concerns. Existing research primarily addresses fairness at specific decision thresholds, using bias metrics like Demographic Parity (DP), Equal Opportunity (EO), and Equalized Odds (EOD) differences. However, threshold-specific metrics may overlook cumulative biases across varying thresholds. In this paper, we adapt fairness metrics traditionally applied in regression models to evaluate cumulative bias across all thresholds in record matching. We propose a novel post-processing calibration method, leveraging optimal transport theory and Wasserstein barycenters, to balance matching scores across demographic groups. This approach treats any matching model as a black box, making it applicable to a wide range of models without access to their training data. Our experiments demonstrate the effectiveness of the calibration method in reducing demographic parity difference in matching scores. To address limitations in reducing EOD and EO differences, we introduce a conditional calibration method, which empirically achieves fairness across widely used benchmarks and state-of-the-art matching methods. This work provides a comprehensive framework for fairness-aware record matching, setting the foundation for more equitable data integration processes.

Evaluating Blocking Biases in Entity Matching

Entity Matching (EM) is crucial for identifying equivalent data entities across different sources, a task that becomes increasingly challenging with the growth and heterogeneity of data. Blocking techniques, which reduce the computational complexity of EM, play a vital role in making this process scalable. Despite advancements in blocking methods, the issue of fairness; where blocking may inadvertently favor certain demographic groups; has been largely overlooked. This study extends traditional blocking metrics to incorporate fairness, providing a framework for assessing bias in blocking techniques. Through experimental analysis, we evaluate the effectiveness and fairness of various blocking methods, offering insights into their potential biases. Our findings highlight the importance of considering fairness in EM, particularly in the blocking phase, to ensure equitable outcomes in data integration tasks.

Threshold-Independent Fair Matching through Score Calibration

Entity Matching (EM) is a critical task in numerous fields, such as healthcare, finance, and public administration, as it identifies records that refer to the same entity within or across different databases. EM faces considerable challenges, particularly with false positives and negatives. These are typically addressed by generating matching scores and apply thresholds to balance false positives and negatives in various contexts. However, adjusting these thresholds can affect the fairness of the outcomes, a critical factor that remains largely overlooked in current fair EM research. The existing body of research on fair EM tends to concentrate on static thresholds, neglecting their critical impact on fairness. To address this, we introduce a new approach in EM using recent metrics for evaluating biases in score based binary classification, particularly through the lens of distributional parity. This approach enables the application of various bias metrics like equalized odds, equal opportunity, and demographic parity without depending on threshold settings. Our experiments with leading matching methods reveal potential biases, and by applying a calibration technique for EM scores using Wasserstein barycenters, we not only mitigate these biases but also preserve accuracy across real world datasets. This paper contributes to the field of fairness in data cleaning, especially within EM, which is a central task in data cleaning, by promoting a method for generating matching scores that reduce biases across different thresholds.

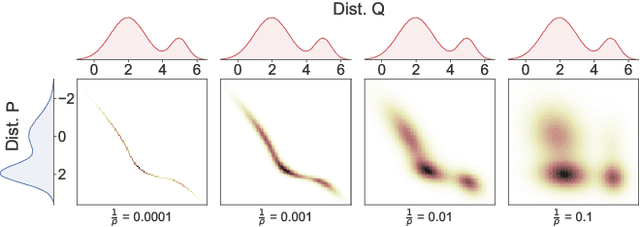
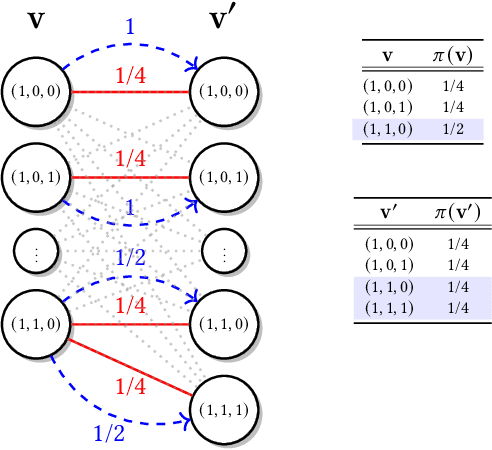
OTClean: Data Cleaning for Conditional Independence Violations using Optimal Transport

Ensuring Conditional Independence (CI) constraints is pivotal for the development of fair and trustworthy machine learning models. In this paper, we introduce \sys, a framework that harnesses optimal transport theory for data repair under CI constraints. Optimal transport theory provides a rigorous framework for measuring the discrepancy between probability distributions, thereby ensuring control over data utility. We formulate the data repair problem concerning CIs as a Quadratically Constrained Linear Program (QCLP) and propose an alternating method for its solution. However, this approach faces scalability issues due to the computational cost associated with computing optimal transport distances, such as the Wasserstein distance. To overcome these scalability challenges, we reframe our problem as a regularized optimization problem, enabling us to develop an iterative algorithm inspired by Sinkhorn's matrix scaling algorithm, which efficiently addresses high-dimensional and large-scale data. Through extensive experiments, we demonstrate the efficacy and efficiency of our proposed methods, showcasing their practical utility in real-world data cleaning and preprocessing tasks. Furthermore, we provide comparisons with traditional approaches, highlighting the superiority of our techniques in terms of preserving data utility while ensuring adherence to the desired CI constraints.

Semi-Oblivious Chase Termination for Linear Existential Rules: An Experimental Study

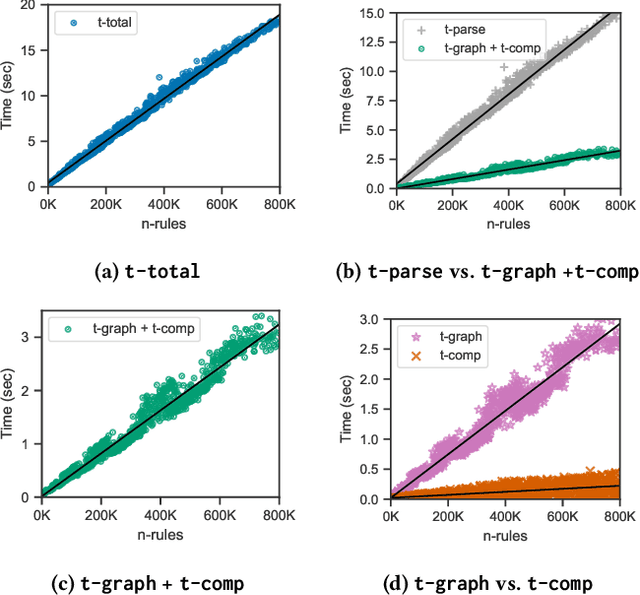
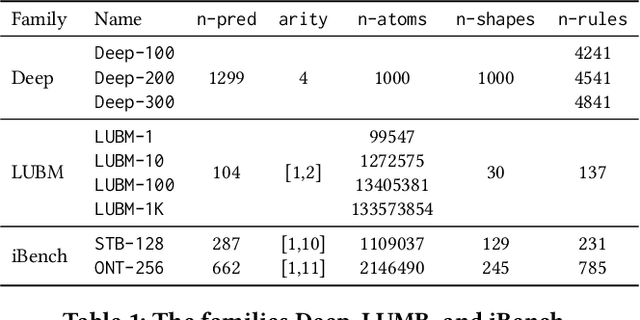
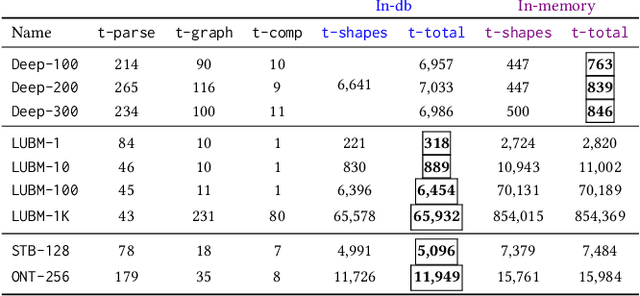
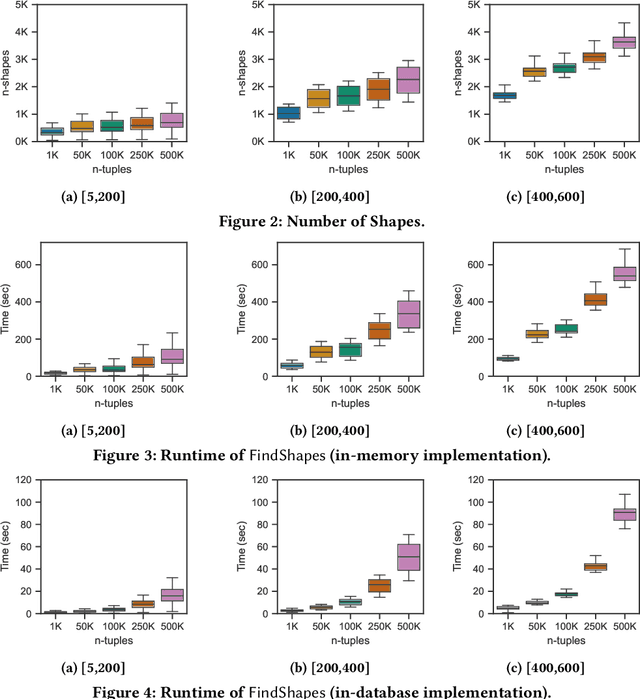
The chase procedure is a fundamental algorithmic tool in databases that allows us to reason with constraints, such as existential rules, with a plethora of applications. It takes as input a database and a set of constraints, and iteratively completes the database as dictated by the constraints. A key challenge, though, is the fact that it may not terminate, which leads to the problem of checking whether it terminates given a database and a set of constraints. In this work, we focus on the semi-oblivious version of the chase, which is well-suited for practical implementations, and linear existential rules, a central class of constraints with several applications. In this setting, there is a mature body of theoretical work that provides syntactic characterizations of when the chase terminates, algorithms for checking chase termination, precise complexity results, and worst-case optimal bounds on the size of the result of the chase (whenever is finite). Our main objective is to experimentally evaluate the existing chase termination algorithms with the aim of understanding which input parameters affect their performance, clarifying whether they can be used in practice, and revealing their performance limitations.

Extending Sticky-Datalog+/- via Finite-Position Selection Functions: Tractability, Algorithms, and Optimization

Weakly-Sticky(WS) Datalog+/- is an expressive member of the family of Datalog+/- program classes that is defined on the basis of the conditions of stickiness and weak-acyclicity. Conjunctive query answering (QA) over the WS programs has been investigated, and its tractability in data complexity has been established. However, the design and implementation of practical QA algorithms and their optimizations have been open. In order to fill this gap, we first study Sticky and WS programs from the point of view of the behavior of the chase procedure. We extend the stickiness property of the chase to that of generalized stickiness of the chase (GSCh) modulo an oracle that selects (and provides) the predicate positions where finitely values appear during the chase. Stickiness modulo a selection function S that provides only a subset of those positions defines sch(S), a semantic subclass of GSCh. Program classes with selection functions include Sticky and WS, and another syntactic class that we introduce and characterize, namely JWS, of jointly-weakly-sticky programs, which contains WS. The selection functions for these last three classes are computable, and no external, possibly non-computable oracle is needed. We propose a bottom-up QA algorithm for programs in the class sch(S), for a general selection function S. As a particular case, we obtain a polynomial-time QA algorithm for JWS and weakly-sticky programs. Unlike WS, JWS turns out to be closed under magic-sets query optimization. As a consequence, both the generic polynomial-time QA algorithm and its magic-set optimization can be particularized and applied to WS.

Ontological Multidimensional Data Models and Contextual Data Qality

Data quality assessment and data cleaning are context-dependent activities. Motivated by this observation, we propose the Ontological Multidimensional Data Model (OMD model), which can be used to model and represent contexts as logic-based ontologies. The data under assessment is mapped into the context, for additional analysis, processing, and quality data extraction. The resulting contexts allow for the representation of dimensions, and multidimensional data quality assessment becomes possible. At the core of a multidimensional context we include a generalized multidimensional data model and a Datalog+/- ontology with provably good properties in terms of query answering. These main components are used to represent dimension hierarchies, dimensional constraints, dimensional rules, and define predicates for quality data specification. Query answering relies upon and triggers navigation through dimension hierarchies, and becomes the basic tool for the extraction of quality data. The OMD model is interesting per se, beyond applications to data quality. It allows for a logic-based, and computationally tractable representation of multidimensional data, extending previous multidimensional data models with additional expressive power and functionalities.

The Ontological Multidimensional Data Model

In this extended abstract we describe, mainly by examples, the main elements of the Ontological Multidimensional Data Model, which considerably extends a relational reconstruction of the multidimensional data model proposed by Hurtado and Mendelzon by means of tuple-generating dependencies, equality-generating dependencies, and negative constraints as found in Datalog+-. We briefly mention some good computational properties of the model.

A Hybrid Approach to Query Answering under Expressive Datalog+/-

Datalog+/- is a family of ontology languages that combine good computational properties with high expressive power. Datalog+/- languages are provably able to capture the most relevant Semantic Web languages. In this paper we consider the class of weakly-sticky (WS) Datalog+/- programs, which allow for certain useful forms of joins in rule bodies as well as extending the well-known class of weakly-acyclic TGDs. So far, only non-deterministic algorithms were known for answering queries on WS Datalog+/- programs. We present novel deterministic query answering algorithms under WS Datalog+/-. In particular, we propose: (1) a bottom-up grounding algorithm based on a query-driven chase, and (2) a hybrid approach based on transforming a WS program into a so-called sticky one, for which query rewriting techniques are known. We discuss how our algorithms can be optimized and effectively applied for query answering in real-world scenarios.

Extending Weakly-Sticky Datalog+/-: Query-Answering Tractability and Optimizations

Weakly-sticky (WS) Datalog+/- is an expressive member of the family of Datalog+/- programs that is based on the syntactic notions of stickiness and weak-acyclicity. Query answering over the WS programs has been investigated, but there is still much work to do on the design and implementation of practical query answering (QA) algorithms and their optimizations. Here, we study sticky and WS programs from the point of view of the behavior of the chase procedure, extending the stickiness property of the chase to that of generalized stickiness of the chase (gsch-property). With this property we specify the semantic class of GSCh programs, which includes sticky and WS programs, and other syntactic subclasses that we identify. In particular, we introduce joint-weakly-sticky (JWS) programs, that include WS programs. We also propose a bottom-up QA algorithm for a range of subclasses of GSCh. The algorithm runs in polynomial time (in data) for JWS programs. Unlike the WS class, JWS is closed under a general magic-sets rewriting procedure for the optimization of programs with existential rules. We apply the magic-sets rewriting in combination with the proposed QA algorithm for the optimization of QA over JWS programs.