Causal DAG Summarization (Full Version)

Causal inference aids researchers in discovering cause-and-effect relationships, leading to scientific insights. Accurate causal estimation requires identifying confounding variables to avoid false discoveries. Pearl's causal model uses causal DAGs to identify confounding variables, but incorrect DAGs can lead to unreliable causal conclusions. However, for high dimensional data, the causal DAGs are often complex beyond human verifiability. Graph summarization is a logical next step, but current methods for general-purpose graph summarization are inadequate for causal DAG summarization. This paper addresses these challenges by proposing a causal graph summarization objective that balances graph simplification for better understanding while retaining essential causal information for reliable inference. We develop an efficient greedy algorithm and show that summary causal DAGs can be directly used for inference and are more robust to misspecification of assumptions, enhancing robustness for causal inference. Experimenting with six real-life datasets, we compared our algorithm to three existing solutions, showing its effectiveness in handling high-dimensional data and its ability to generate summary DAGs that ensure both reliable causal inference and robustness against misspecifications.

Towards Robust Offline Evaluation: A Causal and Information Theoretic Framework for Debiasing Ranking Systems

Evaluating retrieval-ranking systems is crucial for developing high-performing models. While online A/B testing is the gold standard, its high cost and risks to user experience require effective offline methods. However, relying on historical interaction data introduces biases-such as selection, exposure, conformity, and position biases-that distort evaluation metrics, driven by the Missing-Not-At-Random (MNAR) nature of user interactions and favoring popular or frequently exposed items over true user preferences. We propose a novel framework for robust offline evaluation of retrieval-ranking systems, transforming MNAR data into Missing-At-Random (MAR) through reweighting combined with black-box optimization, guided by neural estimation of information-theoretic metrics. Our contributions include (1) a causal formulation for addressing offline evaluation biases, (2) a system-agnostic debiasing framework, and (3) empirical validation of its effectiveness. This framework enables more accurate, fair, and generalizable evaluations, enhancing model assessment before deployment.

A Lightweight Method to Disrupt Memorized Sequences in LLM

Large language models (LLMs) demonstrate impressive capabilities across many tasks yet risk reproducing copyrighted content verbatim, raising legal and ethical concerns. Although methods like differential privacy or neuron editing can reduce memorization, they typically require costly retraining or direct access to model weights and may degrade performance. To address these challenges, we propose TokenSwap, a lightweight, post-hoc approach that replaces the probabilities of grammar-related tokens with those from a small auxiliary model (e.g., DistilGPT-2). We run extensive experiments on commercial grade models such as Pythia-6.9b and LLaMA-3-8b and demonstrate that our method effectively reduces well-known cases of memorized generation by upto 10x with little to no impact on downstream tasks. Our approach offers a uniquely accessible and effective solution to users of real-world systems.

Scalable Out-of-distribution Robustness in the Presence of Unobserved Confounders

We consider the task of out-of-distribution (OOD) generalization, where the distribution shift is due to an unobserved confounder ($Z$) affecting both the covariates ($X$) and the labels ($Y$). In this setting, traditional assumptions of covariate and label shift are unsuitable due to the confounding, which introduces heterogeneity in the predictor, i.e., $\hat{Y} = f_Z(X)$. OOD generalization differs from traditional domain adaptation by not assuming access to the covariate distribution ($X^\text{te}$) of the test samples during training. These conditions create a challenging scenario for OOD robustness: (a) $Z^\text{tr}$ is an unobserved confounder during training, (b) $P^\text{te}{Z} \neq P^\text{tr}{Z}$, (c) $X^\text{te}$ is unavailable during training, and (d) the posterior predictive distribution depends on $P^\text{te}(Z)$, i.e., $\hat{Y} = E_{P^\text{te}(Z)}[f_Z(X)]$. In general, accurate predictions are unattainable in this scenario, and existing literature has proposed complex predictors based on identifiability assumptions that require multiple additional variables. Our work investigates a set of identifiability assumptions that tremendously simplify the predictor, whose resulting elegant simplicity outperforms existing approaches.

Learning from Uncertain Data: From Possible Worlds to Possible Models

We introduce an efficient method for learning linear models from uncertain data, where uncertainty is represented as a set of possible variations in the data, leading to predictive multiplicity. Our approach leverages abstract interpretation and zonotopes, a type of convex polytope, to compactly represent these dataset variations, enabling the symbolic execution of gradient descent on all possible worlds simultaneously. We develop techniques to ensure that this process converges to a fixed point and derive closed-form solutions for this fixed point. Our method provides sound over-approximations of all possible optimal models and viable prediction ranges. We demonstrate the effectiveness of our approach through theoretical and empirical analysis, highlighting its potential to reason about model and prediction uncertainty due to data quality issues in training data.

Enforcing Conditional Independence for Fair Representation Learning and Causal Image Generation

Conditional independence (CI) constraints are critical for defining and evaluating fairness in machine learning, as well as for learning unconfounded or causal representations. Traditional methods for ensuring fairness either blindly learn invariant features with respect to a protected variable (e.g., race when classifying sex from face images) or enforce CI relative to the protected attribute only on the model output (e.g., the sex label). Neither of these methods are effective in enforcing CI in high-dimensional feature spaces. In this paper, we focus on a nascent approach characterizing the CI constraint in terms of two Jensen-Shannon divergence terms, and we extend it to high-dimensional feature spaces using a novel dynamic sampling strategy. In doing so, we introduce a new training paradigm that can be applied to any encoder architecture. We are able to enforce conditional independence of the diffusion autoencoder latent representation with respect to any protected attribute under the equalized odds constraint and show that this approach enables causal image generation with controllable latent spaces. Our experimental results demonstrate that our approach can achieve high accuracy on downstream tasks while upholding equality of odds.

Graph Neural Network based Double Machine Learning Estimator of Network Causal Effects

Our paper addresses the challenge of inferring causal effects in social network data, characterized by complex interdependencies among individuals resulting in challenges such as non-independence of units, interference (where a unit's outcome is affected by neighbors' treatments), and introduction of additional confounding factors from neighboring units. We propose a novel methodology combining graph neural networks and double machine learning, enabling accurate and efficient estimation of direct and peer effects using a single observational social network. Our approach utilizes graph isomorphism networks in conjunction with double machine learning to effectively adjust for network confounders and consistently estimate the desired causal effects. We demonstrate that our estimator is both asymptotically normal and semiparametrically efficient. A comprehensive evaluation against four state-of-the-art baseline methods using three semi-synthetic social network datasets reveals our method's on-par or superior efficacy in precise causal effect estimation. Further, we illustrate the practical application of our method through a case study that investigates the impact of Self-Help Group participation on financial risk tolerance. The results indicate a significant positive direct effect, underscoring the potential of our approach in social network analysis. Additionally, we explore the effects of network sparsity on estimation performance.

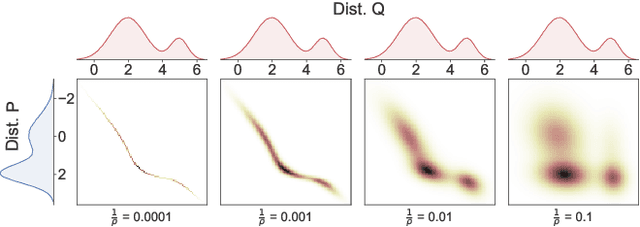
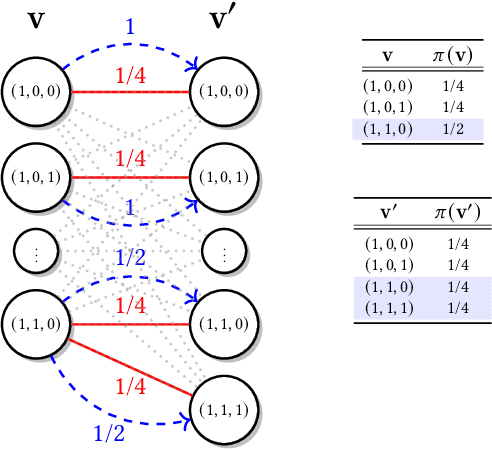
OTClean: Data Cleaning for Conditional Independence Violations using Optimal Transport

Ensuring Conditional Independence (CI) constraints is pivotal for the development of fair and trustworthy machine learning models. In this paper, we introduce \sys, a framework that harnesses optimal transport theory for data repair under CI constraints. Optimal transport theory provides a rigorous framework for measuring the discrepancy between probability distributions, thereby ensuring control over data utility. We formulate the data repair problem concerning CIs as a Quadratically Constrained Linear Program (QCLP) and propose an alternating method for its solution. However, this approach faces scalability issues due to the computational cost associated with computing optimal transport distances, such as the Wasserstein distance. To overcome these scalability challenges, we reframe our problem as a regularized optimization problem, enabling us to develop an iterative algorithm inspired by Sinkhorn's matrix scaling algorithm, which efficiently addresses high-dimensional and large-scale data. Through extensive experiments, we demonstrate the efficacy and efficiency of our proposed methods, showcasing their practical utility in real-world data cleaning and preprocessing tasks. Furthermore, we provide comparisons with traditional approaches, highlighting the superiority of our techniques in terms of preserving data utility while ensuring adherence to the desired CI constraints.

Crab: Learning Certifiably Fair Predictive Models in the Presence of Selection Bias

A recent explosion of research focuses on developing methods and tools for building fair predictive models. However, most of this work relies on the assumption that the training and testing data are representative of the target population on which the model will be deployed. However, real-world training data often suffer from selection bias and are not representative of the target population for many reasons, including the cost and feasibility of collecting and labeling data, historical discrimination, and individual biases. In this paper, we introduce a new framework for certifying and ensuring the fairness of predictive models trained on biased data. We take inspiration from query answering over incomplete and inconsistent databases to present and formalize the problem of consistent range approximation (CRA) of answers to queries about aggregate information for the target population. We aim to leverage background knowledge about the data collection process, biased data, and limited or no auxiliary data sources to compute a range of answers for aggregate queries over the target population that are consistent with available information. We then develop methods that use CRA of such aggregate queries to build predictive models that are certifiably fair on the target population even when no external information about that population is available during training. We evaluate our methods on real data and demonstrate improvements over state of the art. Significantly, we show that enforcing fairness using our methods can lead to predictive models that are not only fair, but more accurate on the target population.

Combining Counterfactuals With Shapley Values To Explain Image Models

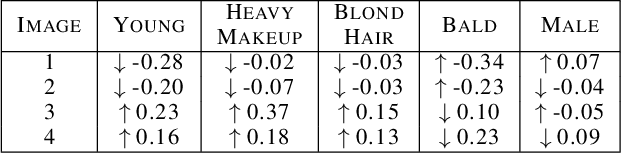
With the widespread use of sophisticated machine learning models in sensitive applications, understanding their decision-making has become an essential task. Models trained on tabular data have witnessed significant progress in explanations of their underlying decision making processes by virtue of having a small number of discrete features. However, applying these methods to high-dimensional inputs such as images is not a trivial task. Images are composed of pixels at an atomic level and do not carry any interpretability by themselves. In this work, we seek to use annotated high-level interpretable features of images to provide explanations. We leverage the Shapley value framework from Game Theory, which has garnered wide acceptance in general XAI problems. By developing a pipeline to generate counterfactuals and subsequently using it to estimate Shapley values, we obtain contrastive and interpretable explanations with strong axiomatic guarantees.