NT-ViT: Neural Transcoding Vision Transformers for EEG-to-fMRI Synthesis

This paper introduces the Neural Transcoding Vision Transformer (\modelname), a generative model designed to estimate high-resolution functional Magnetic Resonance Imaging (fMRI) samples from simultaneous Electroencephalography (EEG) data. A key feature of \modelname is its Domain Matching (DM) sub-module which effectively aligns the latent EEG representations with those of fMRI volumes, enhancing the model's accuracy and reliability. Unlike previous methods that tend to struggle with fidelity and reproducibility of images, \modelname addresses these challenges by ensuring methodological integrity and higher-quality reconstructions which we showcase through extensive evaluation on two benchmark datasets; \modelname outperforms the current state-of-the-art by a significant margin in both cases, e.g. achieving a $10\times$ reduction in RMSE and a $3.14\times$ increase in SSIM on the Oddball dataset. An ablation study also provides insights into the contribution of each component to the model's overall effectiveness. This development is critical in offering a new approach to lessen the time and financial constraints typically linked with high-resolution brain imaging, thereby aiding in the swift and precise diagnosis of neurological disorders. Although it is not a replacement for actual fMRI but rather a step towards making such imaging more accessible, we believe that it represents a pivotal advancement in clinical practice and neuroscience research. Code is available at \url{https://github.com/rom42pla/ntvit}.

Counting Solutions to Conjunctive Queries: Structural and Hybrid Tractability

Counting the number of answers to conjunctive queries is a fundamental problem in databases that, under standard assumptions, does not have an efficient solution. The issue is inherently #P-hard, extending even to classes of acyclic instances. To address this, we pinpoint tractable classes by examining the structural properties of instances and introducing the novel concept of #-hypertree decomposition. We establish the feasibility of counting answers in polynomial time for classes of queries featuring bounded #-hypertree width. Additionally, employing novel techniques from the realm of fixed-parameter computational complexity, we prove that, for bounded arity queries, the bounded #-hypertree width property precisely delineates the frontier of tractability for the counting problem. This result closes an important gap in our understanding of the complexity of such a basic problem for conjunctive queries and, equivalently, for constraint satisfaction problems (CSPs). Drawing upon #-hypertree decompositions, a ''hybrid'' decomposition method emerges. This approach leverages both the structural characteristics of the query and properties intrinsic to the input database, including keys or other (weaker) degree constraints that limit the permissible combinations of values. Intuitively, these features may introduce distinct structural properties that elude identification through the ''worst-possible database'' perspective inherent in purely structural methods.

Tree Projections and Constraint Optimization Problems: Fixed-Parameter Tractability and Parallel Algorithms

Tree projections provide a unifying framework to deal with most structural decomposition methods of constraint satisfaction problems (CSPs). Within this framework, a CSP instance is decomposed into a number of sub-problems, called views, whose solutions are either already available or can be computed efficiently. The goal is to arrange portions of these views in a tree-like structure, called tree projection, which determines an efficiently solvable CSP instance equivalent to the original one. Deciding whether a tree projection exists is NP-hard. Solution methods have therefore been proposed in the literature that do not require a tree projection to be given, and that either correctly decide whether the given CSP instance is satisfiable, or return that a tree projection actually does not exist. These approaches had not been generalized so far on CSP extensions for optimization problems, where the goal is to compute a solution of maximum value/minimum cost. The paper fills the gap, by exhibiting a fixed-parameter polynomial-time algorithm that either disproves the existence of tree projections or computes an optimal solution, with the parameter being the size of the expression of the objective function to be optimized over all possible solutions (and not the size of the whole constraint formula, used in related works). Tractability results are also established for the problem of returning the best K solutions. Finally, parallel algorithms for such optimization problems are proposed and analyzed. Given that the classes of acyclic hypergraphs, hypergraphs of bounded treewidth, and hypergraphs of bounded generalized hypertree width are all covered as special cases of the tree projection framework, the results in this paper directly apply to these classes. These classes are extensively considered in the CSP setting, as well as in conjunctive database query evaluation and optimization.

Computing the Shapley Value in Allocation Problems: Approximations and Bounds, with an Application to the Italian VQR Research Assessment Program

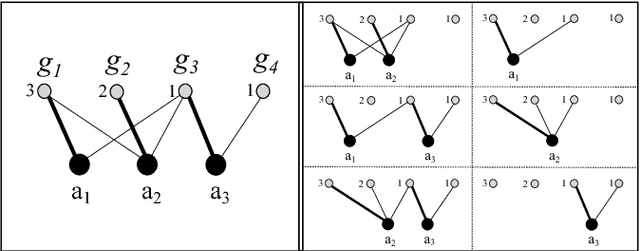
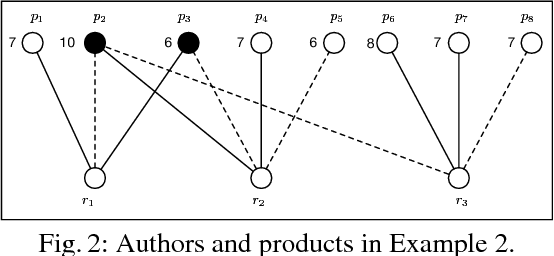
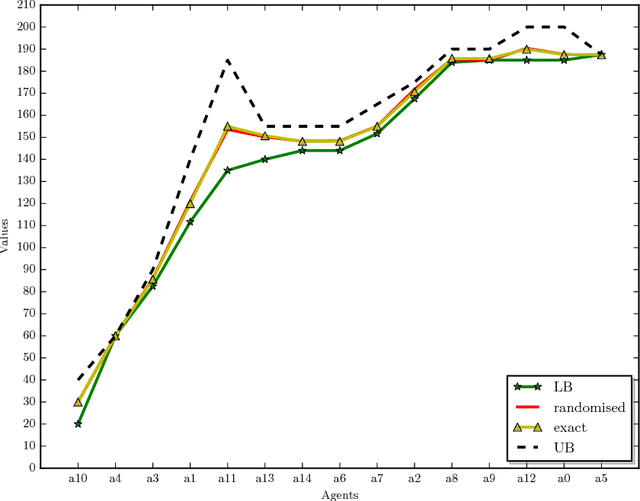
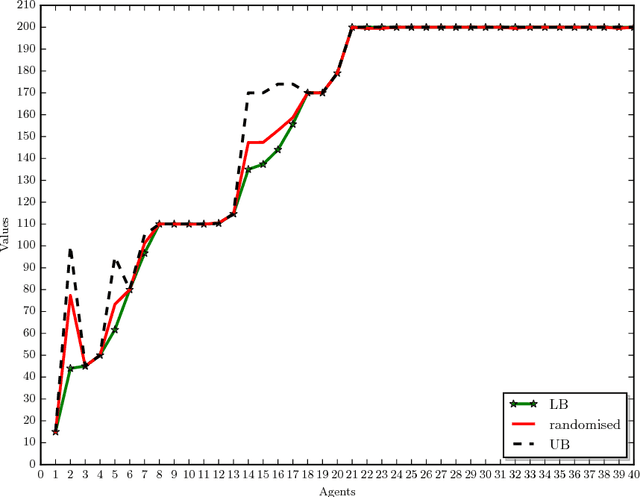
In allocation problems, a given set of goods are assigned to agents in such a way that the social welfare is maximised, that is, the largest possible global worth is achieved. When goods are indivisible, it is possible to use money compensation to perform a fair allocation taking into account the actual contribution of all agents to the social welfare. Coalitional games provide a formal mathematical framework to model such problems, in particular the Shapley value is a solution concept widely used for assigning worths to agents in a fair way. Unfortunately, computing this value is a $\#{\rm P}$-hard problem, so that applying this good theoretical notion is often quite difficult in real-world problems. We describe useful properties that allow us to greatly simplify the instances of allocation problems, without affecting the Shapley value of any player. Moreover, we propose algorithms for computing lower bounds and upper bounds of the Shapley value, which in some cases provide the exact result and that can be combined with approximation algorithms. The proposed techniques have been implemented and tested on a real-world application of allocation problems, namely, the Italian research assessment program, known as VQR. For the large university considered in the experiments, the problem involves thousands of agents and goods (here, researchers and their research products). The algorithms described in the paper are able to compute the Shapley value for most of those agents, and to get a good approximation of the Shapley value for all of them.

Tree Projections and Structural Decomposition Methods: Minimality and Game-Theoretic Characterization

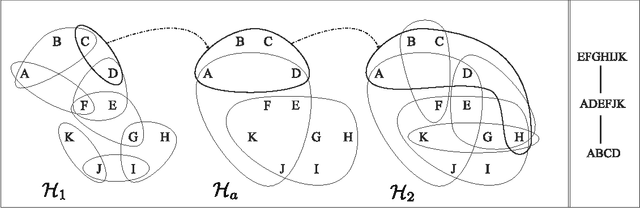
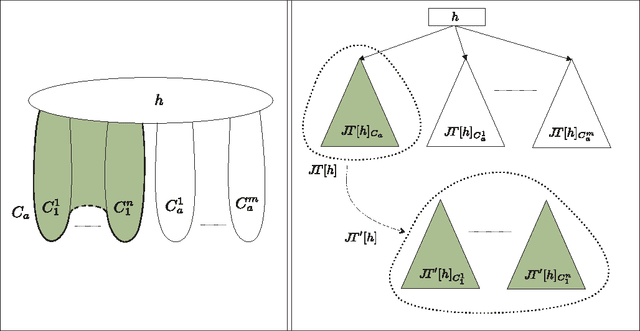
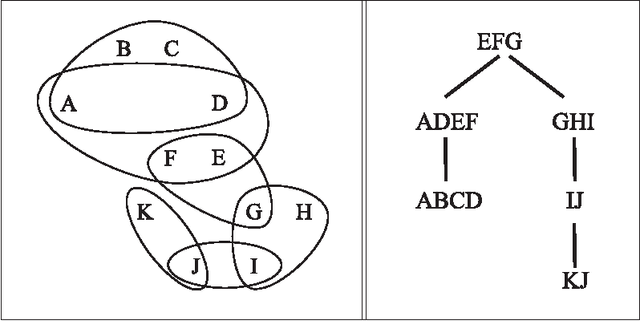
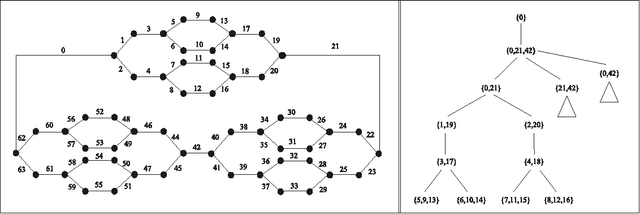
Tree projections provide a mathematical framework that encompasses all the various (purely) structural decomposition methods that have been proposed in the literature to single out classes of nearly-acyclic (hyper)graphs, such as the tree decomposition method, which is the most powerful decomposition method on graphs, and the (generalized) hypertree decomposition method, which is its natural counterpart on arbitrary hypergraphs. The paper analyzes this framework, by focusing in particular on "minimal" tree projections, that is, on tree projections without useless redundancies. First, it is shown that minimal tree projections enjoy a number of properties that are usually required for normal form decompositions in various structural decomposition methods. In particular, they enjoy the same kind of connection properties as (minimal) tree decompositions of graphs, with the result being tight in the light of the negative answer that is provided to the open question about whether they enjoy a slightly stronger notion of connection property, defined to speed-up the computation of hypertree decompositions. Second, it is shown that tree projections admit a natural game-theoretic characterization in terms of the Captain and Robber game. In this game, as for the Robber and Cops game characterizing tree decompositions, the existence of winning strategies implies the existence of monotone ones. As a special case, the Captain and Robber game can be used to characterize the generalized hypertree decomposition method, where such a game-theoretic characterization was missing and asked for. Besides their theoretical interest, these results have immediate algorithmic applications both for the general setting and for structural decomposition methods that can be recast in terms of tree projections.

Tractable Optimization Problems through Hypergraph-Based Structural Restrictions

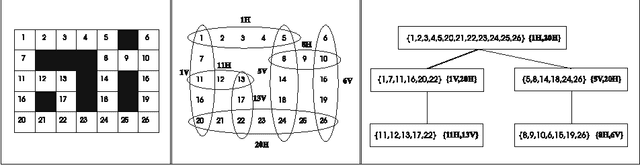
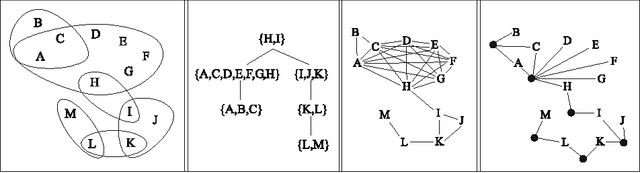
Several variants of the Constraint Satisfaction Problem have been proposed and investigated in the literature for modelling those scenarios where solutions are associated with some given costs. Within these frameworks computing an optimal solution is an NP-hard problem in general; yet, when restricted over classes of instances whose constraint interactions can be modelled via (nearly-)acyclic graphs, this problem is known to be solvable in polynomial time. In this paper, larger classes of tractable instances are singled out, by discussing solution approaches based on exploiting hypergraph acyclicity and, more generally, structural decomposition methods, such as (hyper)tree decompositions.

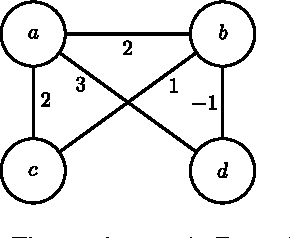
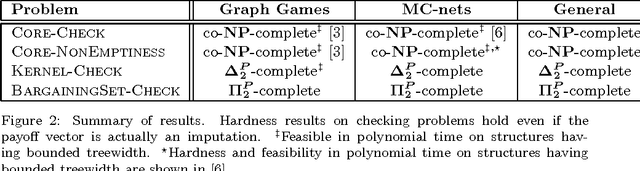
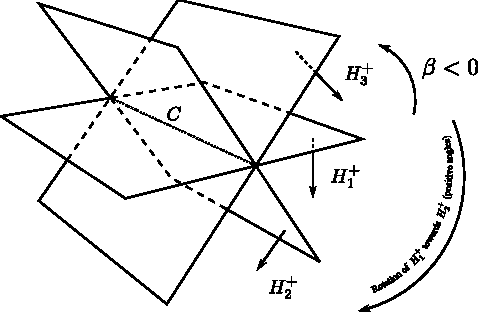
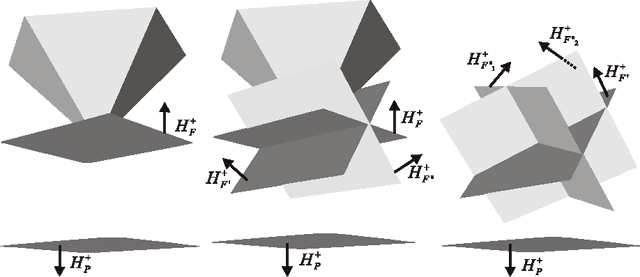
On the Complexity of Core, Kernel, and Bargaining Set

Coalitional games are mathematical models suited to analyze scenarios where players can collaborate by forming coalitions in order to obtain higher worths than by acting in isolation. A fundamental problem for coalitional games is to single out the most desirable outcomes in terms of appropriate notions of worth distributions, which are usually called solution concepts. Motivated by the fact that decisions taken by realistic players cannot involve unbounded resources, recent computer science literature reconsidered the definition of such concepts by advocating the relevance of assessing the amount of resources needed for their computation in terms of their computational complexity. By following this avenue of research, the paper provides a complete picture of the complexity issues arising with three prominent solution concepts for coalitional games with transferable utility, namely, the core, the kernel, and the bargaining set, whenever the game worth-function is represented in some reasonable compact form (otherwise, if the worths of all coalitions are explicitly listed, the input sizes are so large that complexity problems are---artificially---trivial). The starting investigation point is the setting of graph games, about which various open questions were stated in the literature. The paper gives an answer to these questions, and in addition provides new insights on the setting, by characterizing the computational complexity of the three concepts in some relevant generalizations and specializations.

On The Power of Tree Projections: Structural Tractability of Enumerating CSP Solutions

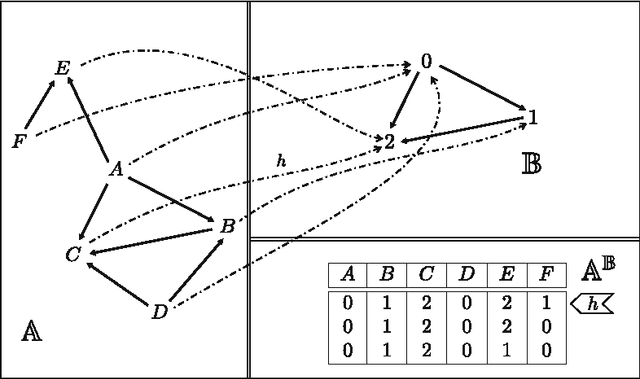
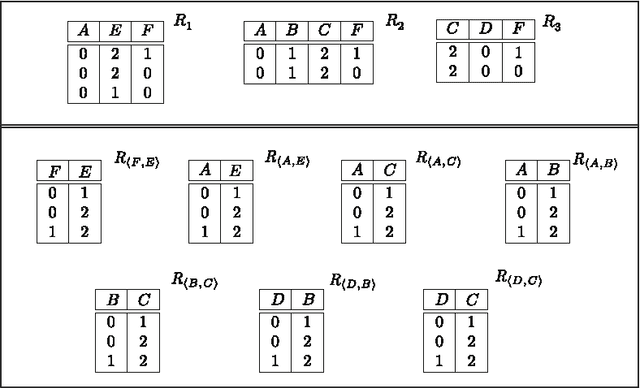
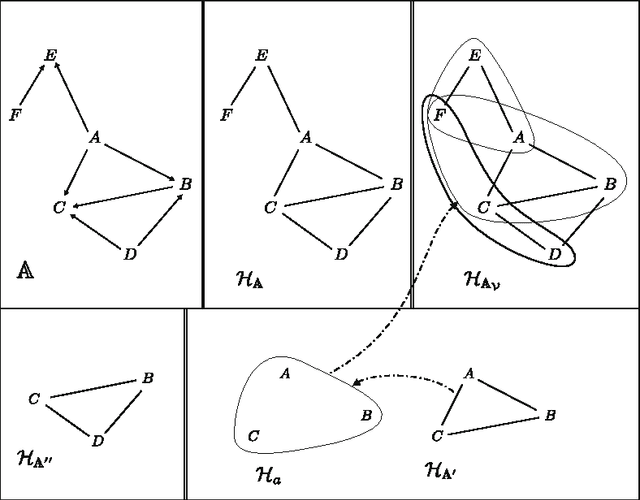
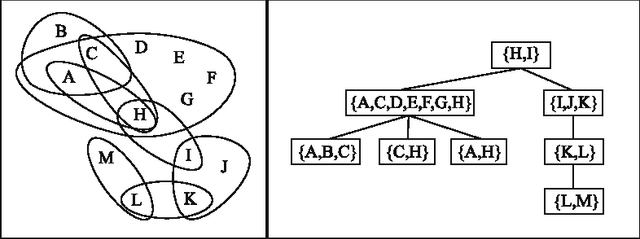
The problem of deciding whether CSP instances admit solutions has been deeply studied in the literature, and several structural tractability results have been derived so far. However, constraint satisfaction comes in practice as a computation problem where the focus is either on finding one solution, or on enumerating all solutions, possibly projected to some given set of output variables. The paper investigates the structural tractability of the problem of enumerating (possibly projected) solutions, where tractability means here computable with polynomial delay (WPD), since in general exponentially many solutions may be computed. A general framework based on the notion of tree projection of hypergraphs is considered, which generalizes all known decomposition methods. Tractability results have been obtained both for classes of structures where output variables are part of their specification, and for classes of structures where computability WPD must be ensured for any possible set of output variables. These results are shown to be tight, by exhibiting dichotomies for classes of structures having bounded arity and where the tree decomposition method is considered.

Abductive Logic Programs with Penalization: Semantics, Complexity and Implementation

Abduction, first proposed in the setting of classical logics, has been studied with growing interest in the logic programming area during the last years. In this paper we study abduction with penalization in the logic programming framework. This form of abductive reasoning, which has not been previously analyzed in logic programming, turns out to represent several relevant problems, including optimization problems, very naturally. We define a formal model for abduction with penalization over logic programs, which extends the abductive framework proposed by Kakas and Mancarella. We address knowledge representation issues, encoding a number of problems in our abductive framework. In particular, we consider some relevant problems, taken from different domains, ranging from optimization theory to diagnosis and planning; their encodings turn out to be simple and elegant in our formalism. We thoroughly analyze the computational complexity of the main problems arising in the context of abduction with penalization from logic programs. Finally, we implement a system supporting the proposed abductive framework on top of the DLV engine. To this end, we design a translation from abduction problems with penalties into logic programs with weak constraints. We prove that this approach is sound and complete.

The DLV System for Knowledge Representation and Reasoning

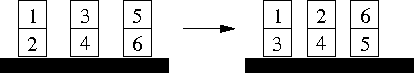
This paper presents the DLV system, which is widely considered the state-of-the-art implementation of disjunctive logic programming, and addresses several aspects. As for problem solving, we provide a formal definition of its kernel language, function-free disjunctive logic programs (also known as disjunctive datalog), extended by weak constraints, which are a powerful tool to express optimization problems. We then illustrate the usage of DLV as a tool for knowledge representation and reasoning, describing a new declarative programming methodology which allows one to encode complex problems (up to $\Delta^P_3$-complete problems) in a declarative fashion. On the foundational side, we provide a detailed analysis of the computational complexity of the language of DLV, and by deriving new complexity results we chart a complete picture of the complexity of this language and important fragments thereof. Furthermore, we illustrate the general architecture of the DLV system which has been influenced by these results. As for applications, we overview application front-ends which have been developed on top of DLV to solve specific knowledge representation tasks, and we briefly describe the main international projects investigating the potential of the system for industrial exploitation. Finally, we report about thorough experimentation and benchmarking, which has been carried out to assess the efficiency of the system. The experimental results confirm the solidity of DLV and highlight its potential for emerging application areas like knowledge management and information integration.