Max Pooling with Vision Transformers reconciles class and shape in weakly supervised semantic segmentation

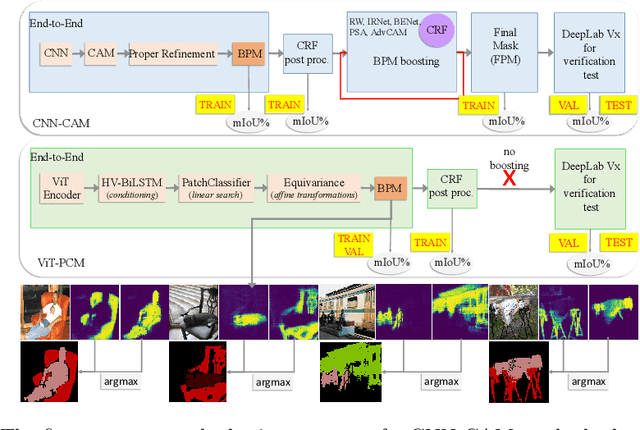
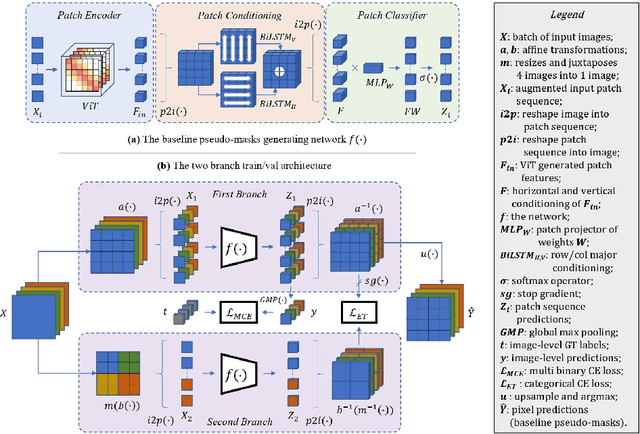
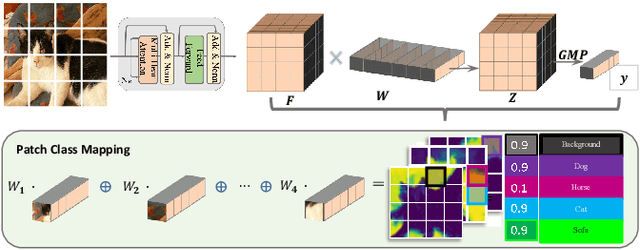
Weakly Supervised Semantic Segmentation (WSSS) research has explored many directions to improve the typical pipeline CNN plus class activation maps (CAM) plus refinements, given the image-class label as the only supervision. Though the gap with the fully supervised methods is reduced, further abating the spread seems unlikely within this framework. On the other hand, WSSS methods based on Vision Transformers (ViT) have not yet explored valid alternatives to CAM. ViT features have been shown to retain a scene layout, and object boundaries in self-supervised learning. To confirm these findings, we prove that the advantages of transformers in self-supervised methods are further strengthened by Global Max Pooling (GMP), which can leverage patch features to negotiate pixel-label probability with class probability. This work proposes a new WSSS method dubbed ViT-PCM (ViT Patch-Class Mapping), not based on CAM. The end-to-end presented network learns with a single optimization process, refined shape and proper localization for segmentation masks. Our model outperforms the state-of-the-art on baseline pseudo-masks (BPM), where we achieve $69.3\%$ mIoU on PascalVOC 2012 $val$ set. We show that our approach has the least set of parameters, though obtaining higher accuracy than all other approaches. In a sentence, quantitative and qualitative results of our method reveal that ViT-PCM is an excellent alternative to CNN-CAM based architectures.

Computing the Shapley Value in Allocation Problems: Approximations and Bounds, with an Application to the Italian VQR Research Assessment Program

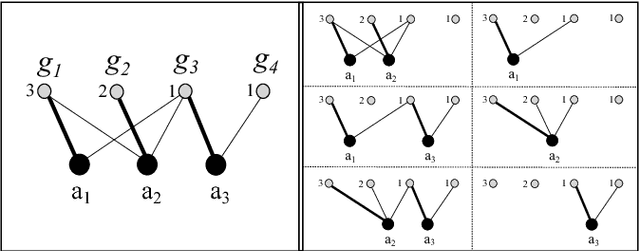
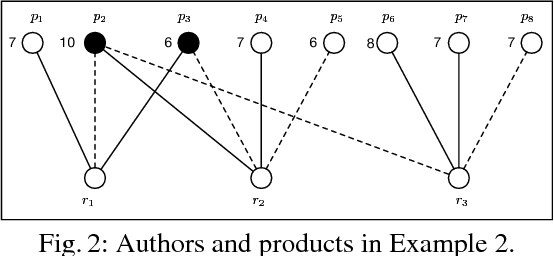
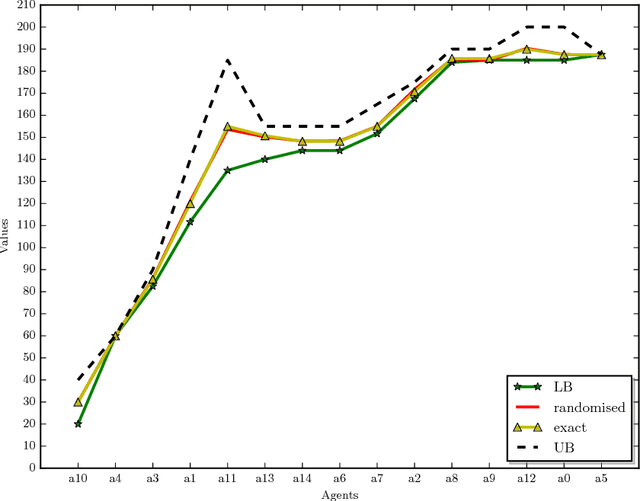
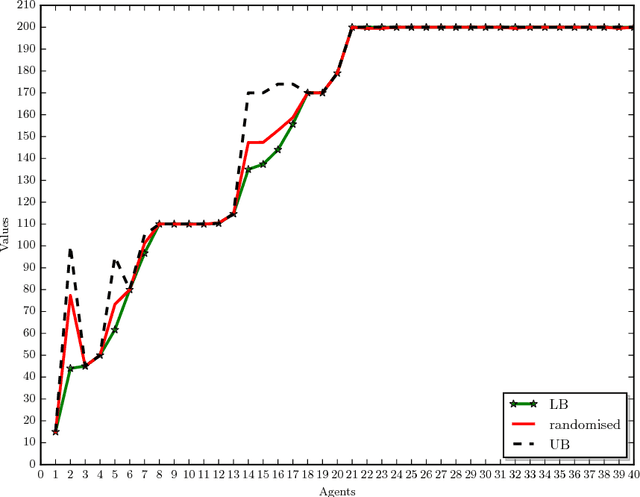
In allocation problems, a given set of goods are assigned to agents in such a way that the social welfare is maximised, that is, the largest possible global worth is achieved. When goods are indivisible, it is possible to use money compensation to perform a fair allocation taking into account the actual contribution of all agents to the social welfare. Coalitional games provide a formal mathematical framework to model such problems, in particular the Shapley value is a solution concept widely used for assigning worths to agents in a fair way. Unfortunately, computing this value is a $\#{\rm P}$-hard problem, so that applying this good theoretical notion is often quite difficult in real-world problems. We describe useful properties that allow us to greatly simplify the instances of allocation problems, without affecting the Shapley value of any player. Moreover, we propose algorithms for computing lower bounds and upper bounds of the Shapley value, which in some cases provide the exact result and that can be combined with approximation algorithms. The proposed techniques have been implemented and tested on a real-world application of allocation problems, namely, the Italian research assessment program, known as VQR. For the large university considered in the experiments, the problem involves thousands of agents and goods (here, researchers and their research products). The algorithms described in the paper are able to compute the Shapley value for most of those agents, and to get a good approximation of the Shapley value for all of them.

On the Complexity of Finding Second-Best Abductive Explanations

While looking for abductive explanations of a given set of manifestations, an ordering between possible solutions is often assumed. The complexity of finding/verifying optimal solutions is already known. In this paper we consider the computational complexity of finding second-best solutions. We consider different orderings, and consider also different possible definitions of what a second-best solution is.

On the size of data structures used in symbolic model checking

Temporal Logic Model Checking is a verification method in which we describe a system, the model, and then we verify whether some properties, expressed in a temporal logic formula, hold in the system. It has many industrial applications. In order to improve performance, some tools allow preprocessing of the model, verifying on-line a set of properties reusing the same compiled model; we prove that the complexity of the Model Checking problem, without any preprocessing or preprocessing the model or the formula in a polynomial data structure, is the same. As a result preprocessing does not always exponentially improve performance. Symbolic Model Checking algorithms work by manipulating sets of states, and these sets are often represented by BDDs. It has been observed that the size of BDDs may grow exponentially as the model and formula increase in size. As a side result, we formally prove that a superpolynomial increase of the size of these BDDs is unavoidable in the worst case. While this exponential growth has been empirically observed, to the best of our knowledge it has never been proved so far in general terms. This result not only holds for all types of BDDs regardless of the variable ordering, but also for more powerful data structures, such as BEDs, RBCs, MTBDDs, and ADDs.

Compilability of Abduction

Abduction is one of the most important forms of reasoning; it has been successfully applied to several practical problems such as diagnosis. In this paper we investigate whether the computational complexity of abduction can be reduced by an appropriate use of preprocessing. This is motivated by the fact that part of the data of the problem (namely, the set of all possible assumptions and the theory relating assumptions and manifestations) are often known before the rest of the problem. In this paper, we show some complexity results about abduction when compilation is allowed.