Can we forget how we learned? Doxastic redundancy in iterated belief revision

How information was acquired may become irrelevant. An obvious case is when something is confirmed many times. In terms of iterated belief revision, a specific revision may become irrelevant in presence of others. Simple repetitions are an example, but not the only case when this happens. Sometimes, a revision becomes redundant even in presence of none equal, or even no else implying it. A necessary and sufficient condition for the redundancy of the first of a sequence of lexicographic revisions is given. The problem is coNP-complete even with two propositional revisions only. Complexity is the same in the Horn case but only with an unbounded number of revisions: it becomes polynomial with two revisions. Lexicographic revisions are not only relevant by themselves, but also because sequences of them are the most compact of the common mechanisms used to represent the state of an iterated revision process. Shortening sequences of lexicographic revisions is shortening the most compact representations of iterated belief revision states.

Natural revision is contingently-conditionalized revision

Natural revision seems so natural: it changes beliefs as little as possible to incorporate new information. Yet, some counterexamples show it wrong. It is so conservative that it never fully believes. It only believes in the current conditions. This is right in some cases and wrong in others. Which is which? The answer requires extending natural revision from simple formulae expressing universal truths (something holds) to conditionals expressing conditional truth (something holds in certain conditions). The extension is based on the basic principles natural revision follows, identified as minimal change, indifference and naivety: change beliefs as little as possible; equate the likeliness of scenarios by default; believe all until contradicted. The extension says that natural revision restricts changes to the current conditions. A comparison with an unrestricting revision shows what exactly the current conditions are. It is not what currently considered true if it contradicts the new information. It includes something more and more unlikely until the new information is at least possible.

Can we forget how we learned? Representing states in iterated belief revision}

The three most common representations of states in iterated belief revision are compared: explicit, by levels and by history. The first is a connected preorder between models, the second is a list of formulae representing equivalence classes, the third is the sequence of the previous revisions. The latter depends on the revision semantics and on history rewriting, and the latter depends on the allowed rewritings. All mechanisms represent all possible states. A rewritten history of lexicographic revision is more efficient than the other considered representations in terms of size with arbitrary history rewritings. Establishing the redundancy of such a history is a mild rewriting. It is coNP-complete in the general case, and is hard even on histories of two revisions or revisions of arbitrary length of Horn formulae, and is polynomial on histories of two Horn formulae. A minor technical result is a polynomial-time algorithm for establishing whether a Horn formula is equivalent to the negation of another Horn formula.

Abductive forgetting

Abductive forgetting is removing variables from a logical formula while maintaining its abductive explanations. It is defined in either of two ways, depending on its intended application. Both differ from the usual forgetting, which maintains consequences rather than explanations. Differently from that, abductive forgetting from a propositional formula may not be expressed by any propositional formula. A necessary and sufficient condition tells when it is. Checking this condition is \P{3}-complete, and is in \P{4} if minimality of explanations is required. A way to guarantee expressibility of abductive forgetting is to switch from propositional to default logic. Another is to introduce new variables.

Superredundancy: A tool for Boolean formula minimization complexity analysis

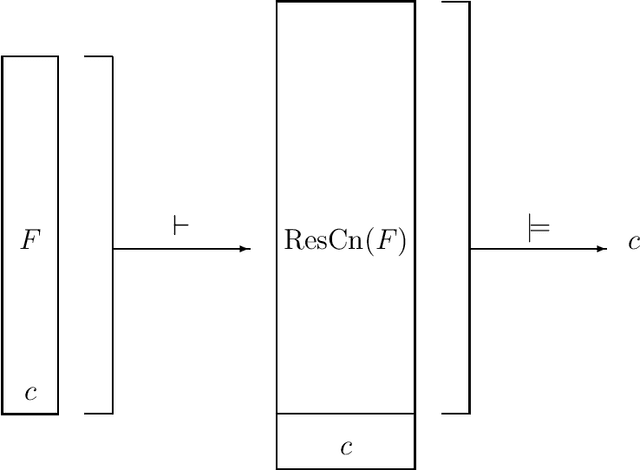
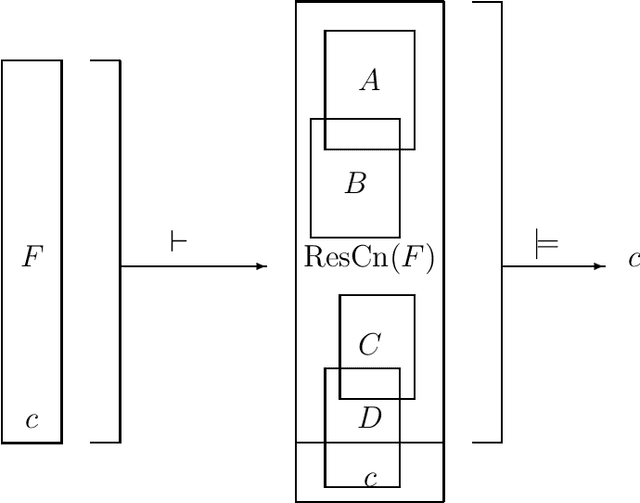
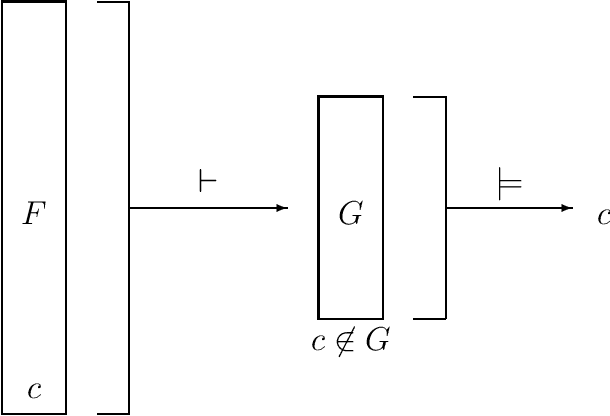
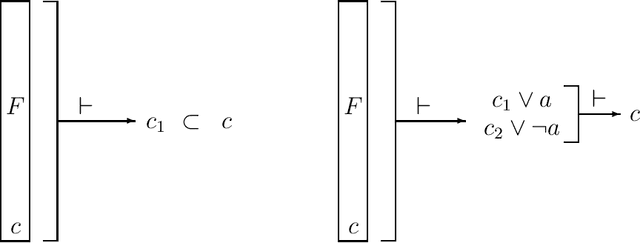
A superredundant clause is a clause that is redundant in the resolution closure of a formula. The converse concept of superirredundancy ensures membership of the clause in all minimal CNF formulae that are equivalent to the given one. This allows for building formulae where some clauses are fixed when minimizing size. An example are proofs of complexity hardness of the problems of minimal formula size. Others are proofs of size when forgetting variables or revising a formula. Most clauses can be made superirredundant by splitting them over a new variable.

Four algorithms for propositional forgetting

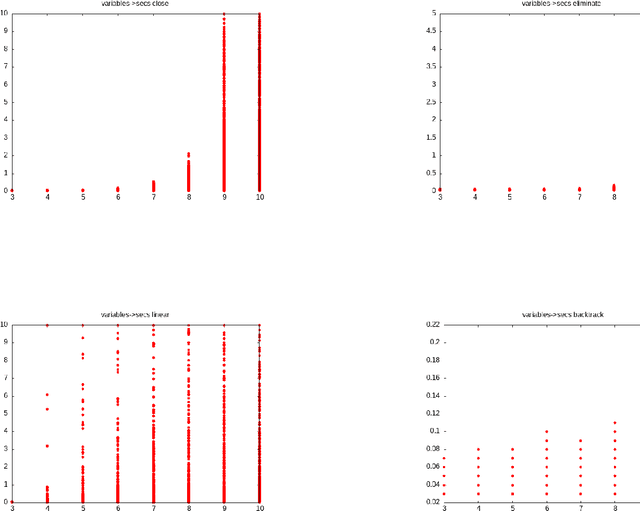
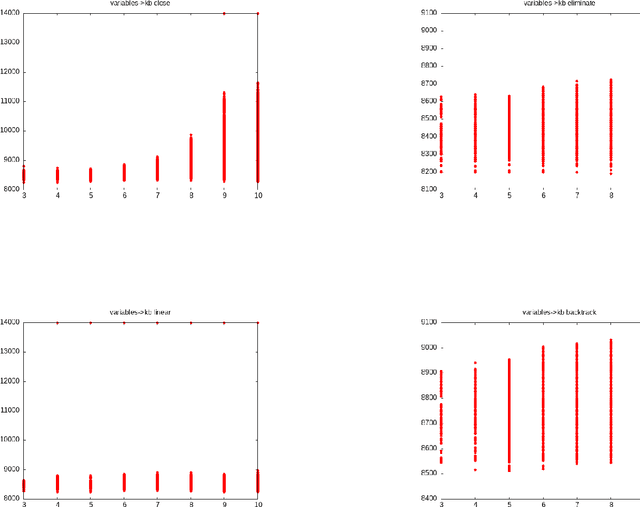
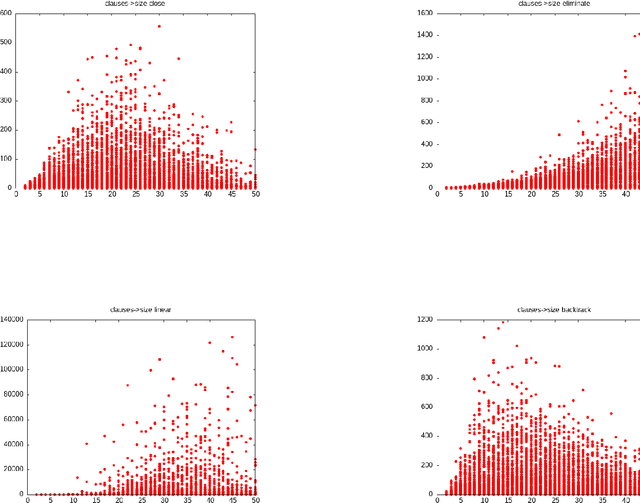
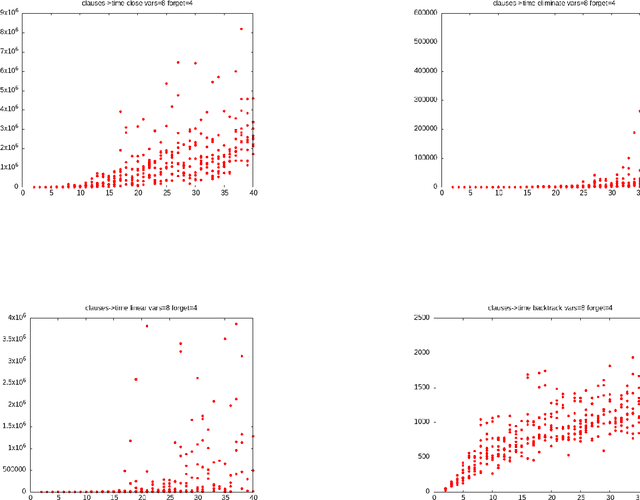
Four algorithms for propositional forgetting are compared. The first performs all possible resolutions and deletes the clauses containing a variable to forget. The second forgets a variable at time by resolving and then deleting all clauses that resolve on that variable. The third outputs the result of all possible linear resolutions on the variables to forget. The fourth generates a clause from the points of contradiction during a backtracking search. The latter emerges as the winner, with the second and first having some role in specific cases. The linear resolution algorithm performs poorly in this implementation.

On Mixed Iterated Revisions

Several forms of iterable belief change exist, differing in the kind of change and its strength: some operators introduce formulae, others remove them; some add formulae unconditionally, others only as additions to the previous beliefs; some only relative to the current situation, others in all possible cases. A sequence of changes may involve several of them: for example, the first step is a revision, the second a contraction and the third a refinement of the previous beliefs. The ten operators considered in this article are shown to be all reducible to three: lexicographic revision, refinement and severe withdrawal. In turn, these three can be expressed in terms of lexicographic revision at the cost of restructuring the sequence. This restructuring needs not to be done explicitly: an algorithm that works on the original sequence is shown. The complexity of mixed sequences of belief change operators is also analyzed. Most of them require only a polynomial number of calls to a satisfiability checker, some are even easier.

Merging with unknown reliability

Merging beliefs depends on the relative reliability of their sources. When unknown, assuming equal reliability is unwarranted. The solution proposed in this article is that every reliability profile is possible, and only what holds according to all is accepted. Alternatively, one source is completely reliable, but which one is unknown. These two cases motivate two existing forms of merging: maxcons-based merging and arbitration.

Reconstructing a single-head formula to facilitate logical forgetting

Logical forgetting may take exponential time in general, but it does not when its input is a single-head propositional definite Horn formula. Single-head means that no variable is the head of multiple clauses. An algorithm to make a formula single-head if possible is shown. It improves over a previous one by being complete: it always finds a single-head formula equivalent to the given one if any.

One head is better than two: a polynomial restriction for propositional definite Horn forgetting

Logical forgetting is NP-complete even in the simple case of propositional Horn formulae. An algorithm previously introduced is improved by changing the input formula before running it. This enlarges the restriction that makes the algorithm polynomial and decreases its running time in other cases. The size of the resulting formula decreases consequently.