Superredundancy: A tool for Boolean formula minimization complexity analysis
Paper and Code
May 02, 2022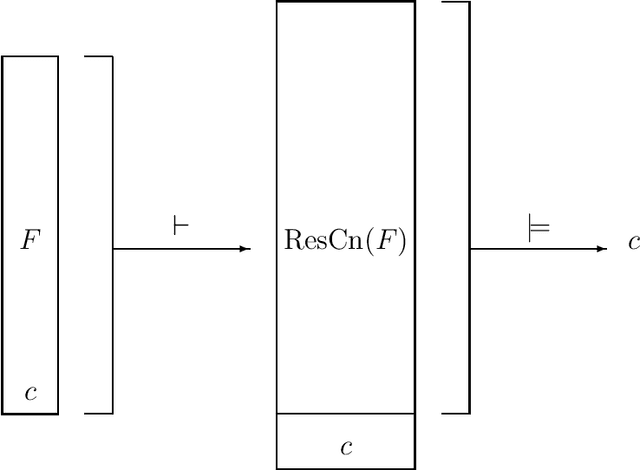
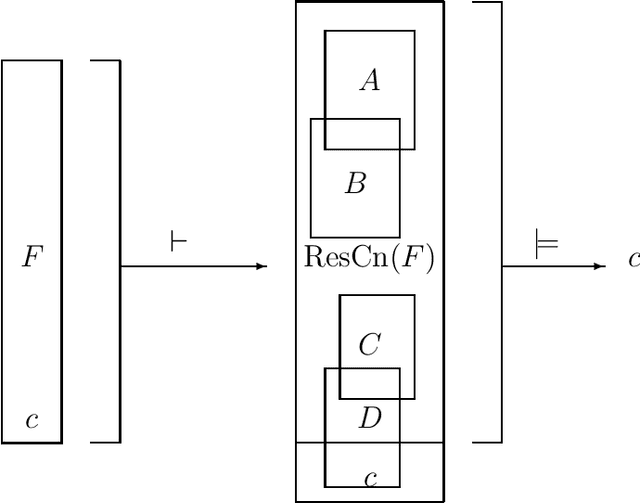
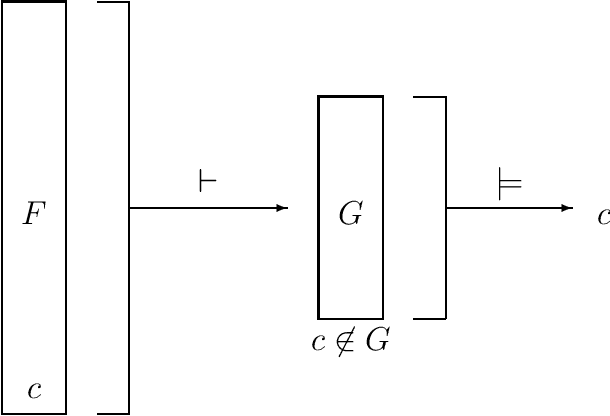
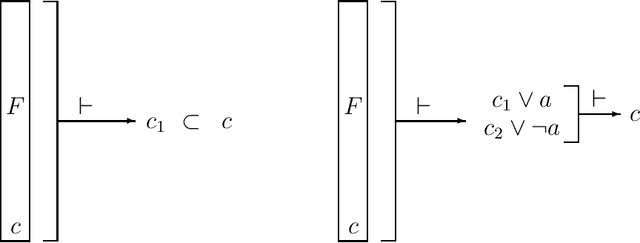
A superredundant clause is a clause that is redundant in the resolution closure of a formula. The converse concept of superirredundancy ensures membership of the clause in all minimal CNF formulae that are equivalent to the given one. This allows for building formulae where some clauses are fixed when minimizing size. An example are proofs of complexity hardness of the problems of minimal formula size. Others are proofs of size when forgetting variables or revising a formula. Most clauses can be made superirredundant by splitting them over a new variable.
* arXiv admin note: substantial text overlap with arXiv:2005.04123
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge