Tree Projections and Structural Decomposition Methods: Minimality and Game-Theoretic Characterization

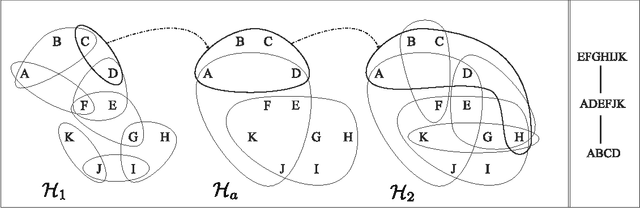
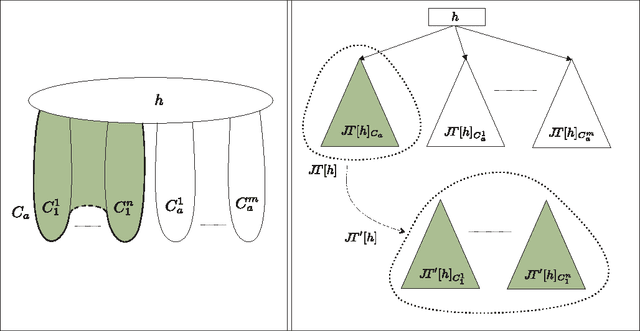
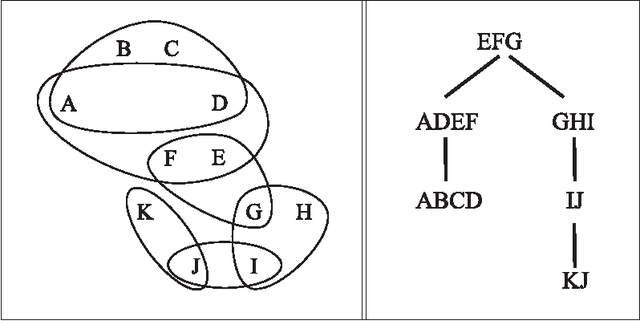
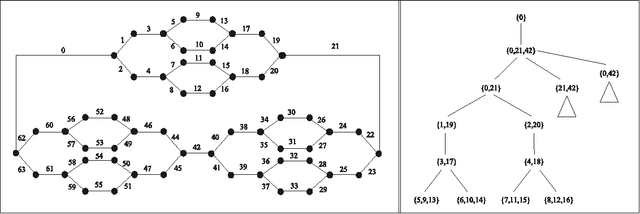
Tree projections provide a mathematical framework that encompasses all the various (purely) structural decomposition methods that have been proposed in the literature to single out classes of nearly-acyclic (hyper)graphs, such as the tree decomposition method, which is the most powerful decomposition method on graphs, and the (generalized) hypertree decomposition method, which is its natural counterpart on arbitrary hypergraphs. The paper analyzes this framework, by focusing in particular on "minimal" tree projections, that is, on tree projections without useless redundancies. First, it is shown that minimal tree projections enjoy a number of properties that are usually required for normal form decompositions in various structural decomposition methods. In particular, they enjoy the same kind of connection properties as (minimal) tree decompositions of graphs, with the result being tight in the light of the negative answer that is provided to the open question about whether they enjoy a slightly stronger notion of connection property, defined to speed-up the computation of hypertree decompositions. Second, it is shown that tree projections admit a natural game-theoretic characterization in terms of the Captain and Robber game. In this game, as for the Robber and Cops game characterizing tree decompositions, the existence of winning strategies implies the existence of monotone ones. As a special case, the Captain and Robber game can be used to characterize the generalized hypertree decomposition method, where such a game-theoretic characterization was missing and asked for. Besides their theoretical interest, these results have immediate algorithmic applications both for the general setting and for structural decomposition methods that can be recast in terms of tree projections.