μ-Net: A Deep Learning-Based Architecture for μ-CT Segmentation

X-ray computed microtomography ({\mu}-CT) is a non-destructive technique that can generate high-resolution 3D images of the internal anatomy of medical and biological samples. These images enable clinicians to examine internal anatomy and gain insights into the disease or anatomical morphology. However, extracting relevant information from 3D images requires semantic segmentation of the regions of interest, which is usually done manually and results time-consuming and tedious. In this work, we propose a novel framework that uses a convolutional neural network (CNN) to automatically segment the full morphology of the heart of Carassius auratus. The framework employs an optimized 2D CNN architecture that can infer a 3D segmentation of the sample, avoiding the high computational cost of a 3D CNN architecture. We tackle the challenges of handling large and high-resoluted image data (over a thousand pixels in each dimension) and a small training database (only three samples) by proposing a standard protocol for data normalization and processing. Moreover, we investigate how the noise, contrast, and spatial resolution of the sample and the training of the architecture are affected by the reconstruction technique, which depends on the number of input images. Experiments show that our framework significantly reduces the time required to segment new samples, allowing a faster microtomography analysis of the Carassius auratus heart shape. Furthermore, our framework can work with any bio-image (biological and medical) from {\mu}-CT with high-resolution and small dataset size

Counting Solutions to Conjunctive Queries: Structural and Hybrid Tractability

Counting the number of answers to conjunctive queries is a fundamental problem in databases that, under standard assumptions, does not have an efficient solution. The issue is inherently #P-hard, extending even to classes of acyclic instances. To address this, we pinpoint tractable classes by examining the structural properties of instances and introducing the novel concept of #-hypertree decomposition. We establish the feasibility of counting answers in polynomial time for classes of queries featuring bounded #-hypertree width. Additionally, employing novel techniques from the realm of fixed-parameter computational complexity, we prove that, for bounded arity queries, the bounded #-hypertree width property precisely delineates the frontier of tractability for the counting problem. This result closes an important gap in our understanding of the complexity of such a basic problem for conjunctive queries and, equivalently, for constraint satisfaction problems (CSPs). Drawing upon #-hypertree decompositions, a ''hybrid'' decomposition method emerges. This approach leverages both the structural characteristics of the query and properties intrinsic to the input database, including keys or other (weaker) degree constraints that limit the permissible combinations of values. Intuitively, these features may introduce distinct structural properties that elude identification through the ''worst-possible database'' perspective inherent in purely structural methods.

A New Deep Learning and XAI-Based Algorithm for Features Selection in Genomics

In the field of functional genomics, the analysis of gene expression profiles through Machine and Deep Learning is increasingly providing meaningful insight into a number of diseases. The paper proposes a novel algorithm to perform Feature Selection on genomic-scale data, which exploits the reconstruction capabilities of autoencoders and an ad-hoc defined Explainable Artificial Intelligence-based score in order to select the most informative genes for diagnosis, prognosis, and precision medicine. Results of the application on a Chronic Lymphocytic Leukemia dataset evidence the effectiveness of the algorithm, by identifying and suggesting a set of meaningful genes for further medical investigation.

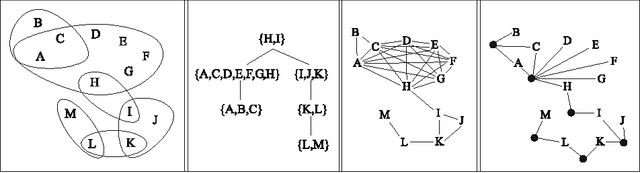
Tree Projections and Structural Decomposition Methods: Minimality and Game-Theoretic Characterization

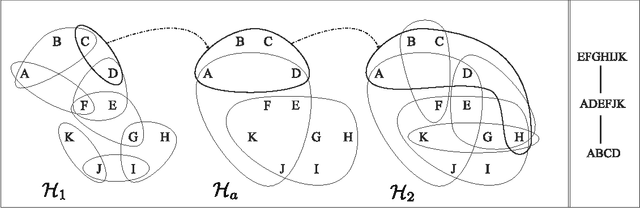
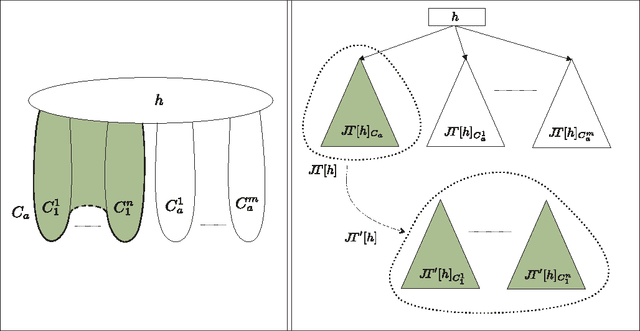
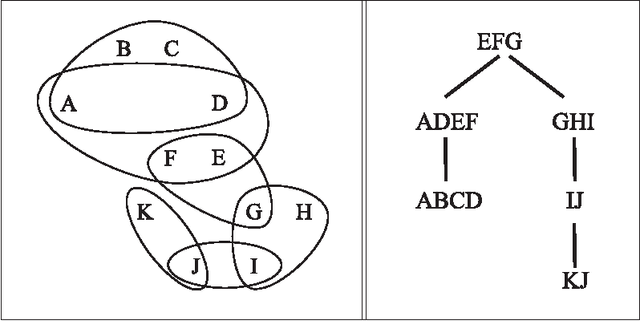
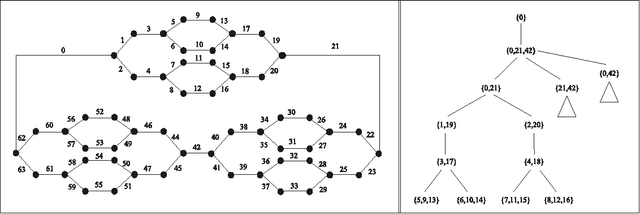
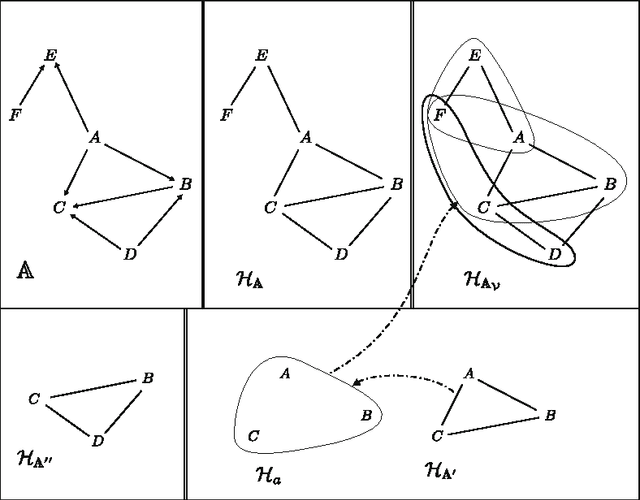
Tree projections provide a mathematical framework that encompasses all the various (purely) structural decomposition methods that have been proposed in the literature to single out classes of nearly-acyclic (hyper)graphs, such as the tree decomposition method, which is the most powerful decomposition method on graphs, and the (generalized) hypertree decomposition method, which is its natural counterpart on arbitrary hypergraphs. The paper analyzes this framework, by focusing in particular on "minimal" tree projections, that is, on tree projections without useless redundancies. First, it is shown that minimal tree projections enjoy a number of properties that are usually required for normal form decompositions in various structural decomposition methods. In particular, they enjoy the same kind of connection properties as (minimal) tree decompositions of graphs, with the result being tight in the light of the negative answer that is provided to the open question about whether they enjoy a slightly stronger notion of connection property, defined to speed-up the computation of hypertree decompositions. Second, it is shown that tree projections admit a natural game-theoretic characterization in terms of the Captain and Robber game. In this game, as for the Robber and Cops game characterizing tree decompositions, the existence of winning strategies implies the existence of monotone ones. As a special case, the Captain and Robber game can be used to characterize the generalized hypertree decomposition method, where such a game-theoretic characterization was missing and asked for. Besides their theoretical interest, these results have immediate algorithmic applications both for the general setting and for structural decomposition methods that can be recast in terms of tree projections.

Tractable Optimization Problems through Hypergraph-Based Structural Restrictions

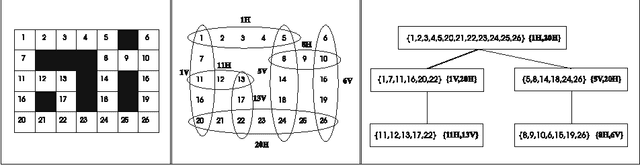
Several variants of the Constraint Satisfaction Problem have been proposed and investigated in the literature for modelling those scenarios where solutions are associated with some given costs. Within these frameworks computing an optimal solution is an NP-hard problem in general; yet, when restricted over classes of instances whose constraint interactions can be modelled via (nearly-)acyclic graphs, this problem is known to be solvable in polynomial time. In this paper, larger classes of tractable instances are singled out, by discussing solution approaches based on exploiting hypergraph acyclicity and, more generally, structural decomposition methods, such as (hyper)tree decompositions.

Magic Sets for Disjunctive Datalog Programs

In this paper, a new technique for the optimization of (partially) bound queries over disjunctive Datalog programs with stratified negation is presented. The technique exploits the propagation of query bindings and extends the Magic Set (MS) optimization technique. An important feature of disjunctive Datalog is nonmonotonicity, which calls for nondeterministic implementations, such as backtracking search. A distinguishing characteristic of the new method is that the optimization can be exploited also during the nondeterministic phase. In particular, after some assumptions have been made during the computation, parts of the program may become irrelevant to a query under these assumptions. This allows for dynamic pruning of the search space. In contrast, the effect of the previously defined MS methods for disjunctive Datalog is limited to the deterministic portion of the process. In this way, the potential performance gain by using the proposed method can be exponential, as could be observed empirically. The correctness of MS is established thanks to a strong relationship between MS and unfounded sets that has not been studied in the literature before. This knowledge allows for extending the method also to programs with stratified negation in a natural way. The proposed method has been implemented in DLV and various experiments have been conducted. Experimental results on synthetic data confirm the utility of MS for disjunctive Datalog, and they highlight the computational gain that may be obtained by the new method w.r.t. the previously proposed MS methods for disjunctive Datalog programs. Further experiments on real-world data show the benefits of MS within an application scenario that has received considerable attention in recent years, the problem of answering user queries over possibly inconsistent databases originating from integration of autonomous sources of information.

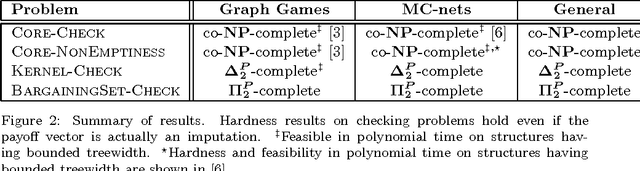
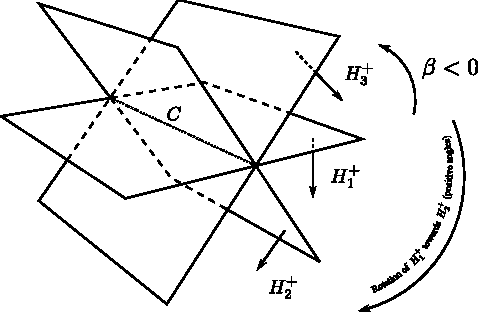
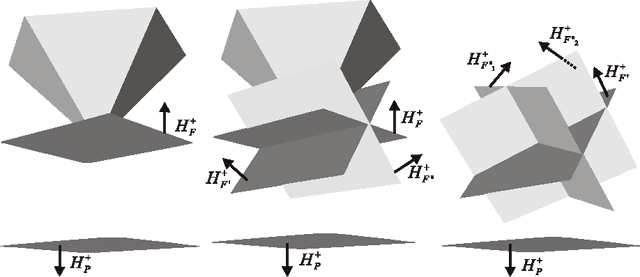
On the Complexity of Core, Kernel, and Bargaining Set

Coalitional games are mathematical models suited to analyze scenarios where players can collaborate by forming coalitions in order to obtain higher worths than by acting in isolation. A fundamental problem for coalitional games is to single out the most desirable outcomes in terms of appropriate notions of worth distributions, which are usually called solution concepts. Motivated by the fact that decisions taken by realistic players cannot involve unbounded resources, recent computer science literature reconsidered the definition of such concepts by advocating the relevance of assessing the amount of resources needed for their computation in terms of their computational complexity. By following this avenue of research, the paper provides a complete picture of the complexity issues arising with three prominent solution concepts for coalitional games with transferable utility, namely, the core, the kernel, and the bargaining set, whenever the game worth-function is represented in some reasonable compact form (otherwise, if the worths of all coalitions are explicitly listed, the input sizes are so large that complexity problems are---artificially---trivial). The starting investigation point is the setting of graph games, about which various open questions were stated in the literature. The paper gives an answer to these questions, and in addition provides new insights on the setting, by characterizing the computational complexity of the three concepts in some relevant generalizations and specializations.

On The Power of Tree Projections: Structural Tractability of Enumerating CSP Solutions

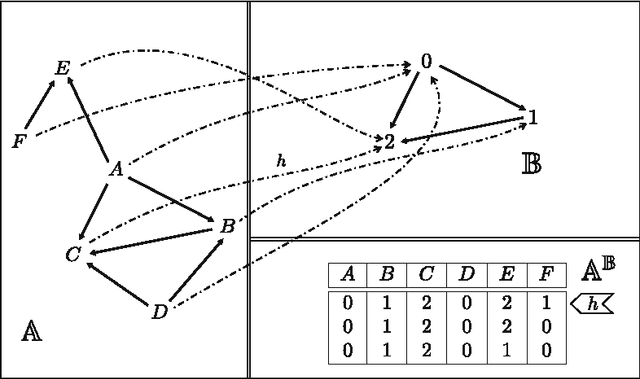
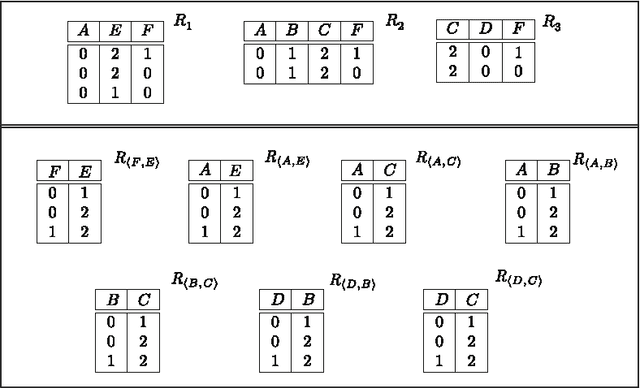
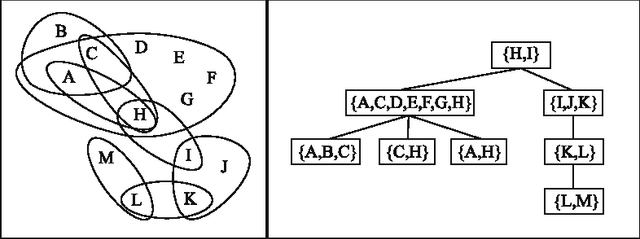
The problem of deciding whether CSP instances admit solutions has been deeply studied in the literature, and several structural tractability results have been derived so far. However, constraint satisfaction comes in practice as a computation problem where the focus is either on finding one solution, or on enumerating all solutions, possibly projected to some given set of output variables. The paper investigates the structural tractability of the problem of enumerating (possibly projected) solutions, where tractability means here computable with polynomial delay (WPD), since in general exponentially many solutions may be computed. A general framework based on the notion of tree projection of hypergraphs is considered, which generalizes all known decomposition methods. Tractability results have been obtained both for classes of structures where output variables are part of their specification, and for classes of structures where computability WPD must be ensured for any possible set of output variables. These results are shown to be tight, by exhibiting dichotomies for classes of structures having bounded arity and where the tree decomposition method is considered.

Outlier Detection by Logic Programming

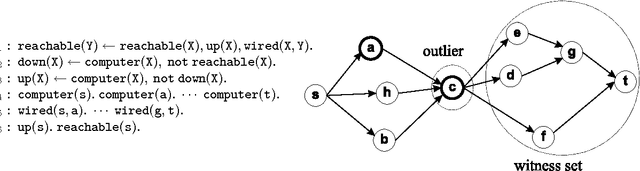
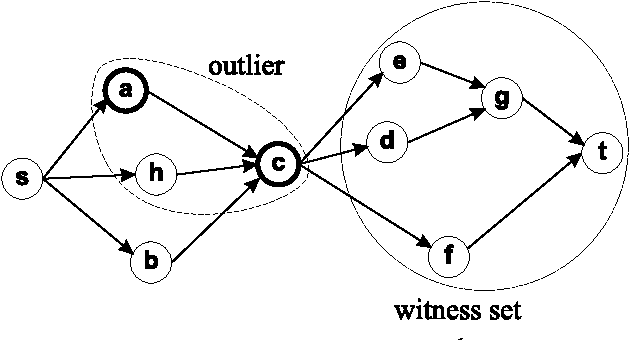
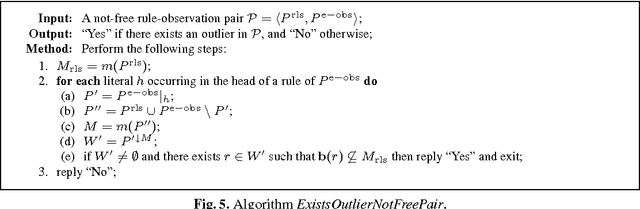
The development of effective knowledge discovery techniques has become in the recent few years a very active research area due to the important impact it has in several relevant application areas. One interesting task thereof is that of singling out anomalous individuals from a given population, e.g., to detect rare events in time-series analysis settings, or to identify objects whose behavior is deviant w.r.t. a codified standard set of "social" rules. Such exceptional individuals are usually referred to as outliers in the literature. Recently, outlier detection has also emerged as a relevant KR&R problem. In this paper, we formally state the concept of outliers by generalizing in several respects an approach recently proposed in the context of default logic, for instance, by having outliers not being restricted to single individuals but, rather, in the more general case, to correspond to entire (sub)theories. We do that within the context of logic programming and, mainly through examples, we discuss its potential practical impact in applications. The formalization we propose is a novel one and helps in shedding some light on the real nature of outliers. Moreover, as a major contribution of this work, we illustrate the exploitation of minimality criteria in outlier detection. The computational complexity of outlier detection problems arising in this novel setting is thoroughly investigated and accounted for in the paper as well. Finally, we also propose a rewriting algorithm that transforms any outlier detection problem into an equivalent inference problem under the stable model semantics, thereby making outlier computation effective and realizable on top of any stable model solver.

Minimal founded semantics for disjunctive logic programs and deductive databases

In this paper, we propose a variant of stable model semantics for disjunctive logic programming and deductive databases. The semantics, called minimal founded, generalizes stable model semantics for normal (i.e. non disjunctive) programs but differs from disjunctive stable model semantics (the extension of stable model semantics for disjunctive programs). Compared with disjunctive stable model semantics, minimal founded semantics seems to be more intuitive, it gives meaning to programs which are meaningless under stable model semantics and is no harder to compute. More specifically, minimal founded semantics differs from stable model semantics only for disjunctive programs having constraint rules or rules working as constraints. We study the expressive power of the semantics and show that for general disjunctive datalog programs it has the same power as disjunctive stable model semantics.