Outlier Detection by Logic Programming

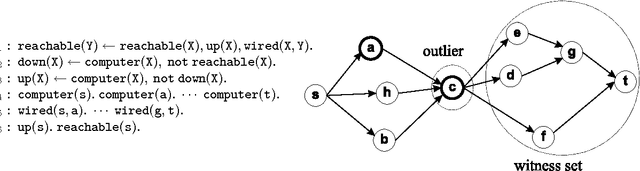
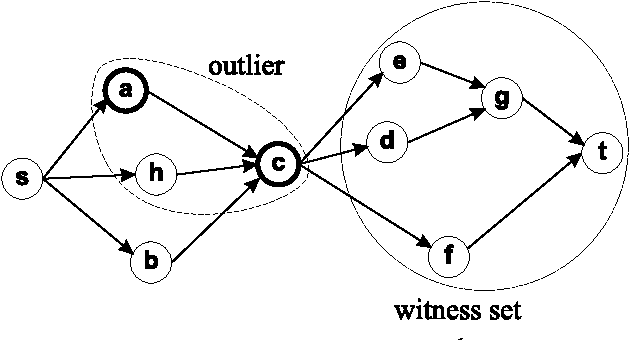
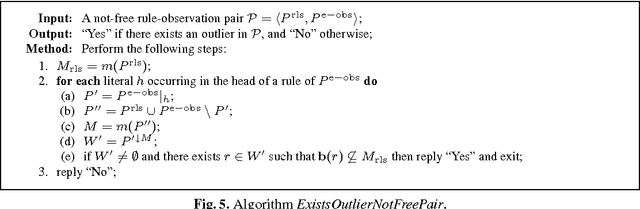
The development of effective knowledge discovery techniques has become in the recent few years a very active research area due to the important impact it has in several relevant application areas. One interesting task thereof is that of singling out anomalous individuals from a given population, e.g., to detect rare events in time-series analysis settings, or to identify objects whose behavior is deviant w.r.t. a codified standard set of "social" rules. Such exceptional individuals are usually referred to as outliers in the literature. Recently, outlier detection has also emerged as a relevant KR&R problem. In this paper, we formally state the concept of outliers by generalizing in several respects an approach recently proposed in the context of default logic, for instance, by having outliers not being restricted to single individuals but, rather, in the more general case, to correspond to entire (sub)theories. We do that within the context of logic programming and, mainly through examples, we discuss its potential practical impact in applications. The formalization we propose is a novel one and helps in shedding some light on the real nature of outliers. Moreover, as a major contribution of this work, we illustrate the exploitation of minimality criteria in outlier detection. The computational complexity of outlier detection problems arising in this novel setting is thoroughly investigated and accounted for in the paper as well. Finally, we also propose a rewriting algorithm that transforms any outlier detection problem into an equivalent inference problem under the stable model semantics, thereby making outlier computation effective and realizable on top of any stable model solver.