Reconstruction Error-based Anomaly Detection with Few Outlying Examples

Reconstruction error-based neural architectures constitute a classical deep learning approach to anomaly detection which has shown great performances. It consists in training an Autoencoder to reconstruct a set of examples deemed to represent the normality and then to point out as anomalies those data that show a sufficiently large reconstruction error. Unfortunately, these architectures often become able to well reconstruct also the anomalies in the data. This phenomenon is more evident when there are anomalies in the training set. In particular when these anomalies are labeled, a setting called semi-supervised, the best way to train Autoencoders is to ignore anomalies and minimize the reconstruction error on normal data. The goal of this work is to investigate approaches to allow reconstruction error-based architectures to instruct the model to put known anomalies outside of the domain description of the normal data. Specifically, our strategy exploits a limited number of anomalous examples to increase the contrast between the reconstruction error associated with normal examples and those associated with both known and unknown anomalies, thus enhancing anomaly detection performances. The experiments show that this new procedure achieves better performances than the standard Autoencoder approach and the main deep learning techniques for semi-supervised anomaly detection.

CFOF: A Concentration Free Measure for Anomaly Detection

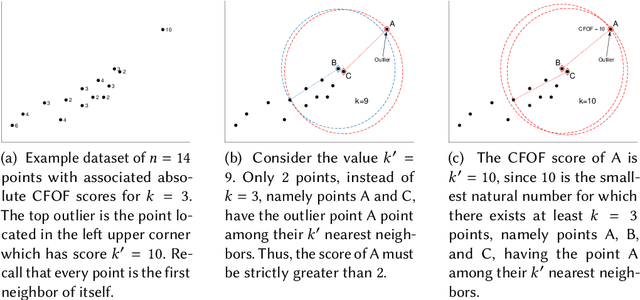
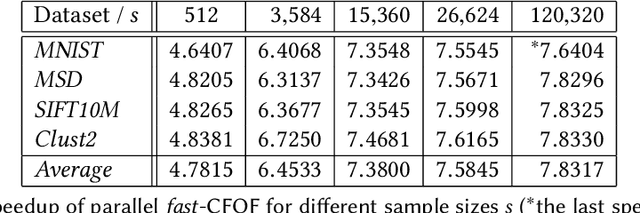
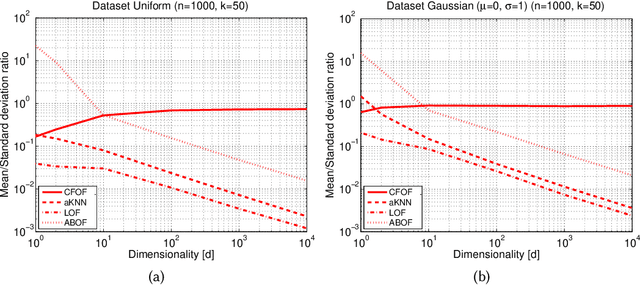
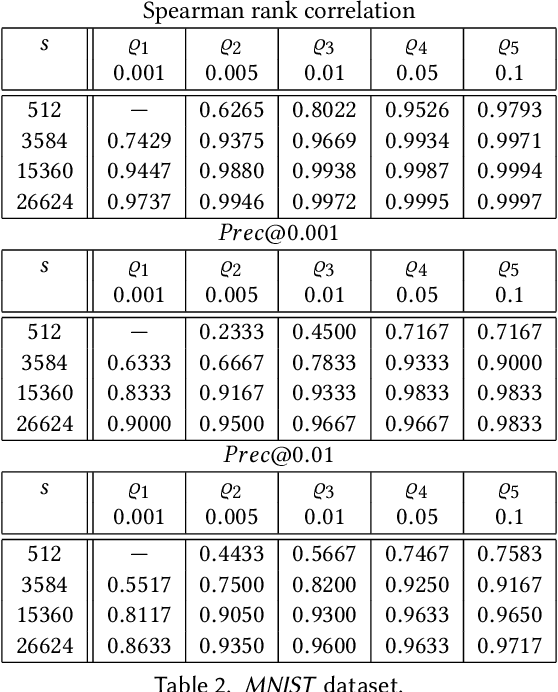
We present a novel notion of outlier, called the Concentration Free Outlier Factor, or CFOF. As a main contribution, we formalize the notion of concentration of outlier scores and theoretically prove that CFOF does not concentrate in the Euclidean space for any arbitrary large dimensionality. To the best of our knowledge, there are no other proposals of data analysis measures related to the Euclidean distance for which it has been provided theoretical evidence that they are immune to the concentration effect. We determine the closed form of the distribution of CFOF scores in arbitrarily large dimensionalities and show that the CFOF score of a point depends on its squared norm standard score and on the kurtosis of the data distribution, thus providing a clear and statistically founded characterization of this notion. Moreover, we leverage this closed form to provide evidence that the definition does not suffer of the hubness problem affecting other measures. We prove that the number of CFOF outliers coming from each cluster is proportional to cluster size and kurtosis, a property that we call semi-locality. We determine that semi-locality characterizes existing reverse nearest neighbor-based outlier definitions, thus clarifying the exact nature of their observed local behavior. We also formally prove that classical distance-based and density-based outliers concentrate both for bounded and unbounded sample sizes and for fixed and variable values of the neighborhood parameter. We introduce the fast-CFOF algorithm for detecting outliers in large high-dimensional dataset. The algorithm has linear cost, supports multi-resolution analysis, and is embarrassingly parallel. Experiments highlight that the technique is able to efficiently process huge datasets and to deal even with large values of the neighborhood parameter, to avoid concentration, and to obtain excellent accuracy.

On the Tractability of Minimal Model Computation for Some CNF Theories

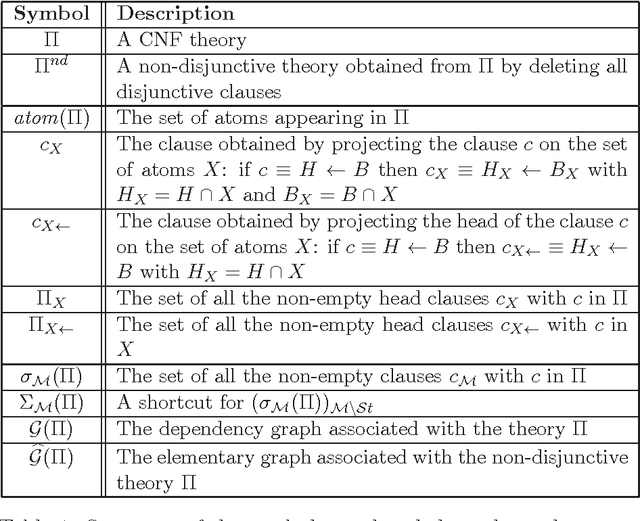
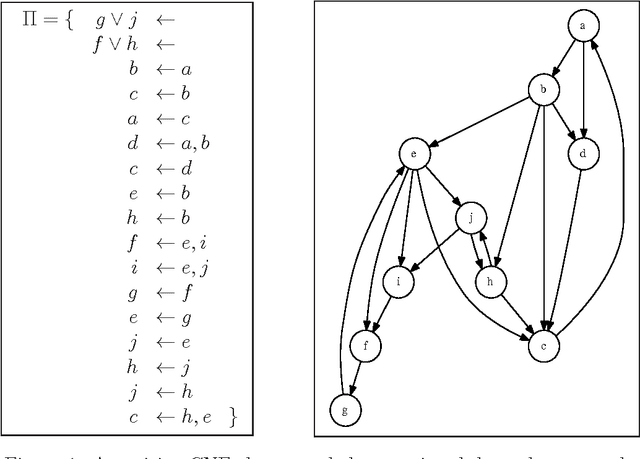
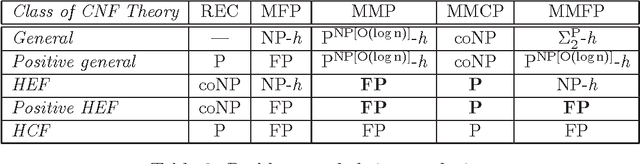
Designing algorithms capable of efficiently constructing minimal models of CNFs is an important task in AI. This paper provides new results along this research line and presents new algorithms for performing minimal model finding and checking over positive propositional CNFs and model minimization over propositional CNFs. An algorithmic schema, called the Generalized Elimination Algorithm (GEA) is presented, that computes a minimal model of any positive CNF. The schema generalizes the Elimination Algorithm (EA) [BP97], which computes a minimal model of positive head-cycle-free (HCF) CNF theories. While the EA always runs in polynomial time in the size of the input HCF CNF, the complexity of the GEA depends on the complexity of the specific eliminating operator invoked therein, which may in general turn out to be exponential. Therefore, a specific eliminating operator is defined by which the GEA computes, in polynomial time, a minimal model for a class of CNF that strictly includes head-elementary-set-free (HEF) CNF theories [GLL06], which form, in their turn, a strict superset of HCF theories. Furthermore, in order to deal with the high complexity associated with recognizing HEF theories, an "incomplete" variant of the GEA (called IGEA) is proposed: the resulting schema, once instantiated with an appropriate elimination operator, always constructs a model of the input CNF, which is guaranteed to be minimal if the input theory is HEF. In the light of the above results, the main contribution of this work is the enlargement of the tractability frontier for the minimal model finding and checking and the model minimization problems.

Outlying Property Detection with Numerical Attributes

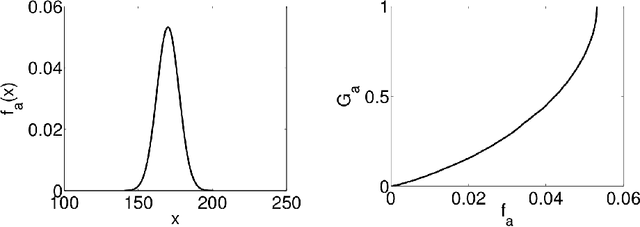
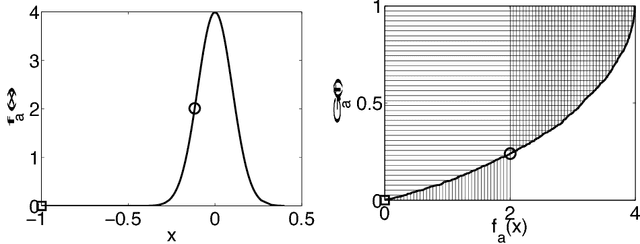
The outlying property detection problem is the problem of discovering the properties distinguishing a given object, known in advance to be an outlier in a database, from the other database objects. In this paper, we analyze the problem within a context where numerical attributes are taken into account, which represents a relevant case left open in the literature. We introduce a measure to quantify the degree the outlierness of an object, which is associated with the relative likelihood of the value, compared to the to the relative likelihood of other objects in the database. As a major contribution, we present an efficient algorithm to compute the outlierness relative to significant subsets of the data. The latter subsets are characterized in a "rule-based" fashion, and hence the basis for the underlying explanation of the outlierness.

Uncertain Nearest Neighbor Classification

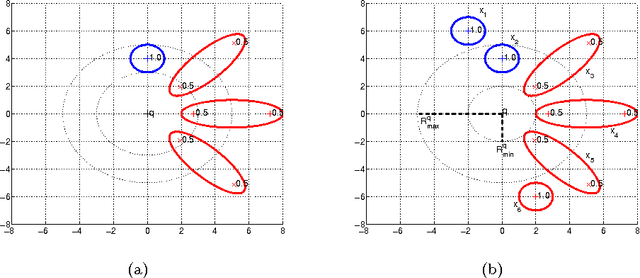
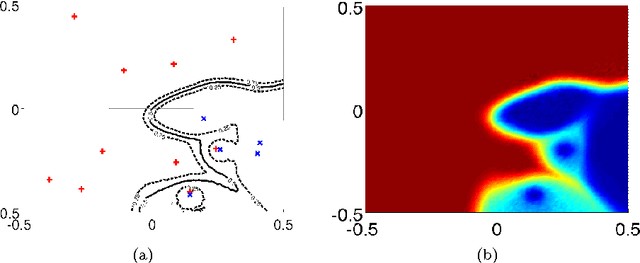
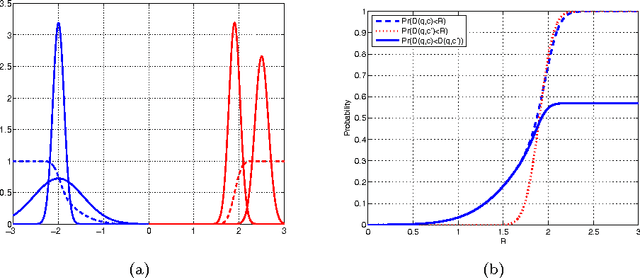
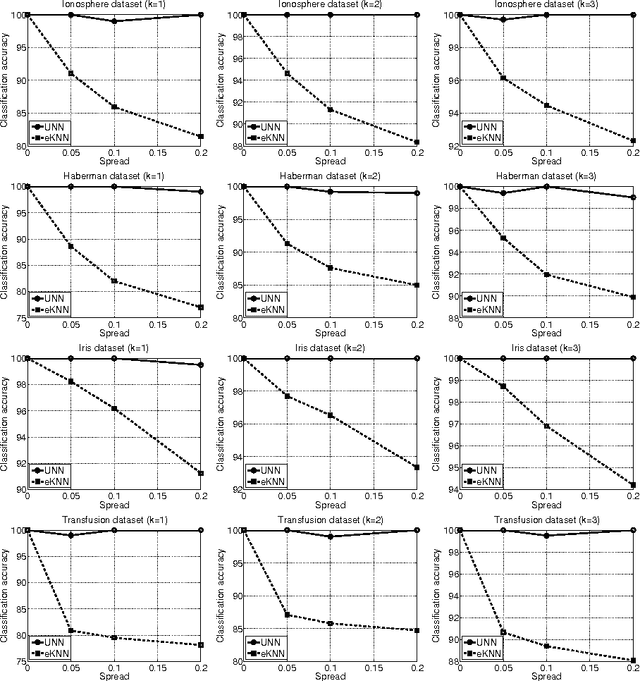
This work deals with the problem of classifying uncertain data. With this aim the Uncertain Nearest Neighbor (UNN) rule is here introduced, which represents the generalization of the deterministic nearest neighbor rule to the case in which uncertain objects are available. The UNN rule relies on the concept of nearest neighbor class, rather than on that of nearest neighbor object. The nearest neighbor class of a test object is the class that maximizes the probability of providing its nearest neighbor. It is provided evidence that the former concept is much more powerful than the latter one in the presence of uncertainty, in that it correctly models the right semantics of the nearest neighbor decision rule when applied to the uncertain scenario. An effective and efficient algorithm to perform uncertain nearest neighbor classification of a generic (un)certain test object is designed, based on properties that greatly reduce the temporal cost associated with nearest neighbor class probability computation. Experimental results are presented, showing that the UNN rule is effective and efficient in classifying uncertain data.

Outlier Detection by Logic Programming

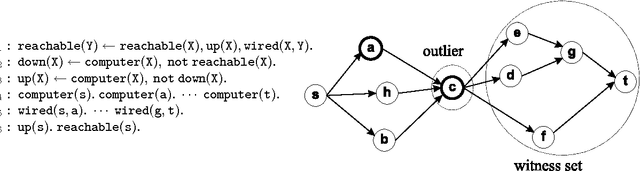
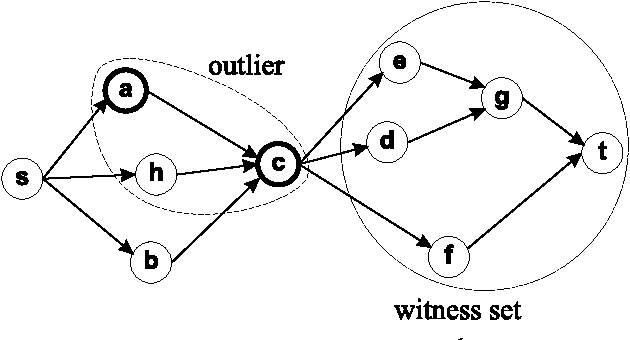
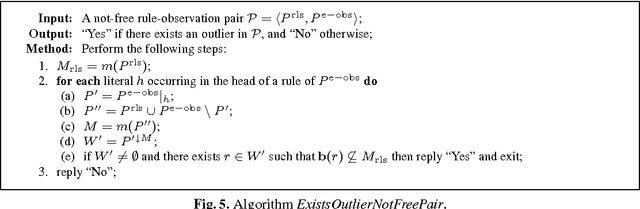
The development of effective knowledge discovery techniques has become in the recent few years a very active research area due to the important impact it has in several relevant application areas. One interesting task thereof is that of singling out anomalous individuals from a given population, e.g., to detect rare events in time-series analysis settings, or to identify objects whose behavior is deviant w.r.t. a codified standard set of "social" rules. Such exceptional individuals are usually referred to as outliers in the literature. Recently, outlier detection has also emerged as a relevant KR&R problem. In this paper, we formally state the concept of outliers by generalizing in several respects an approach recently proposed in the context of default logic, for instance, by having outliers not being restricted to single individuals but, rather, in the more general case, to correspond to entire (sub)theories. We do that within the context of logic programming and, mainly through examples, we discuss its potential practical impact in applications. The formalization we propose is a novel one and helps in shedding some light on the real nature of outliers. Moreover, as a major contribution of this work, we illustrate the exploitation of minimality criteria in outlier detection. The computational complexity of outlier detection problems arising in this novel setting is thoroughly investigated and accounted for in the paper as well. Finally, we also propose a rewriting algorithm that transforms any outlier detection problem into an equivalent inference problem under the stable model semantics, thereby making outlier computation effective and realizable on top of any stable model solver.