Reconstruction Error-based Anomaly Detection with Few Outlying Examples

Reconstruction error-based neural architectures constitute a classical deep learning approach to anomaly detection which has shown great performances. It consists in training an Autoencoder to reconstruct a set of examples deemed to represent the normality and then to point out as anomalies those data that show a sufficiently large reconstruction error. Unfortunately, these architectures often become able to well reconstruct also the anomalies in the data. This phenomenon is more evident when there are anomalies in the training set. In particular when these anomalies are labeled, a setting called semi-supervised, the best way to train Autoencoders is to ignore anomalies and minimize the reconstruction error on normal data. The goal of this work is to investigate approaches to allow reconstruction error-based architectures to instruct the model to put known anomalies outside of the domain description of the normal data. Specifically, our strategy exploits a limited number of anomalous examples to increase the contrast between the reconstruction error associated with normal examples and those associated with both known and unknown anomalies, thus enhancing anomaly detection performances. The experiments show that this new procedure achieves better performances than the standard Autoencoder approach and the main deep learning techniques for semi-supervised anomaly detection.

On the Tractability of Minimal Model Computation for Some CNF Theories

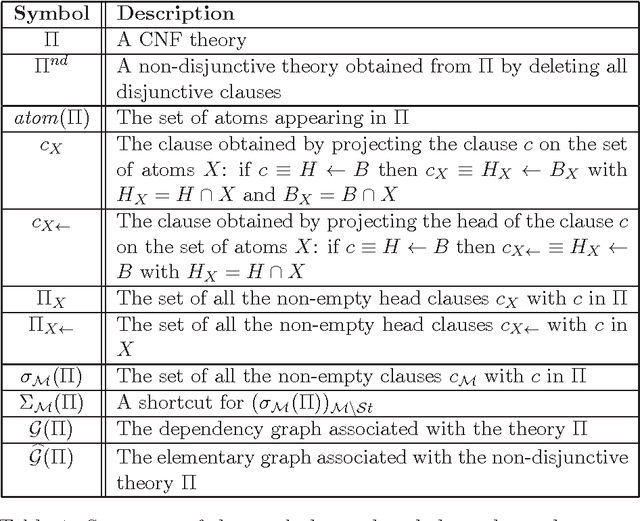
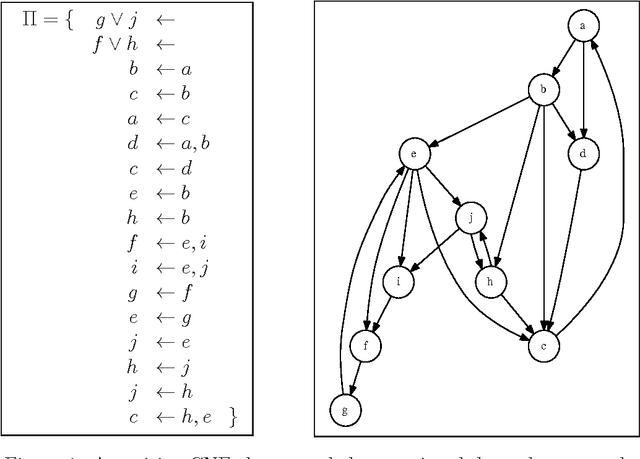
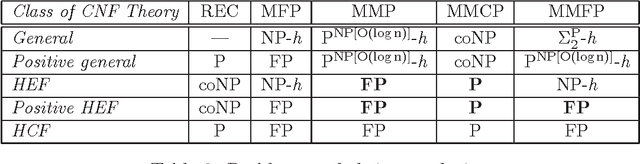
Designing algorithms capable of efficiently constructing minimal models of CNFs is an important task in AI. This paper provides new results along this research line and presents new algorithms for performing minimal model finding and checking over positive propositional CNFs and model minimization over propositional CNFs. An algorithmic schema, called the Generalized Elimination Algorithm (GEA) is presented, that computes a minimal model of any positive CNF. The schema generalizes the Elimination Algorithm (EA) [BP97], which computes a minimal model of positive head-cycle-free (HCF) CNF theories. While the EA always runs in polynomial time in the size of the input HCF CNF, the complexity of the GEA depends on the complexity of the specific eliminating operator invoked therein, which may in general turn out to be exponential. Therefore, a specific eliminating operator is defined by which the GEA computes, in polynomial time, a minimal model for a class of CNF that strictly includes head-elementary-set-free (HEF) CNF theories [GLL06], which form, in their turn, a strict superset of HCF theories. Furthermore, in order to deal with the high complexity associated with recognizing HEF theories, an "incomplete" variant of the GEA (called IGEA) is proposed: the resulting schema, once instantiated with an appropriate elimination operator, always constructs a model of the input CNF, which is guaranteed to be minimal if the input theory is HEF. In the light of the above results, the main contribution of this work is the enlargement of the tractability frontier for the minimal model finding and checking and the model minimization problems.

Outlying Property Detection with Numerical Attributes

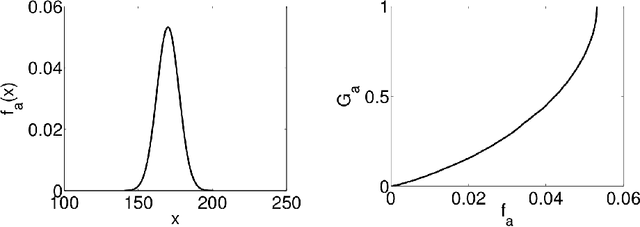
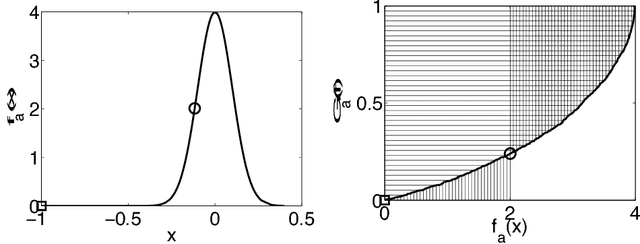
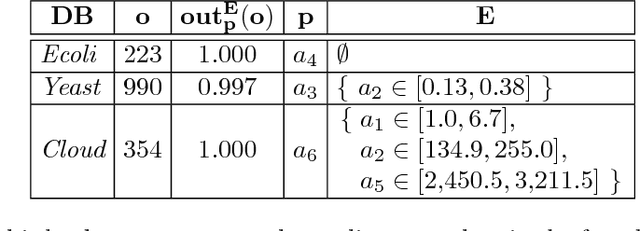
The outlying property detection problem is the problem of discovering the properties distinguishing a given object, known in advance to be an outlier in a database, from the other database objects. In this paper, we analyze the problem within a context where numerical attributes are taken into account, which represents a relevant case left open in the literature. We introduce a measure to quantify the degree the outlierness of an object, which is associated with the relative likelihood of the value, compared to the to the relative likelihood of other objects in the database. As a major contribution, we present an efficient algorithm to compute the outlierness relative to significant subsets of the data. The latter subsets are characterized in a "rule-based" fashion, and hence the basis for the underlying explanation of the outlierness.

Uncertain Nearest Neighbor Classification

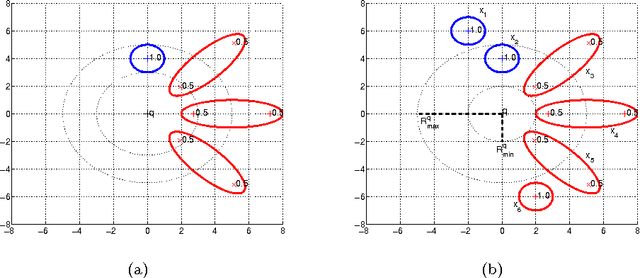
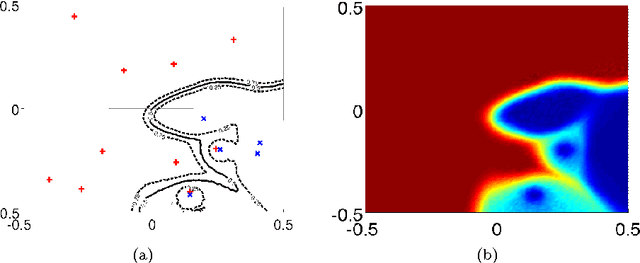
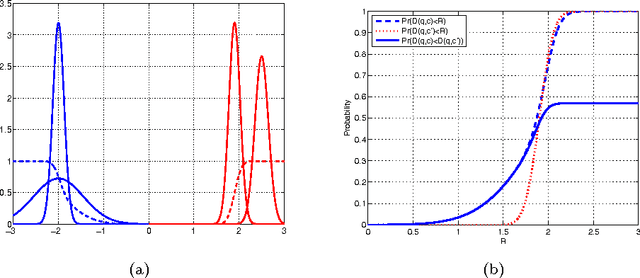
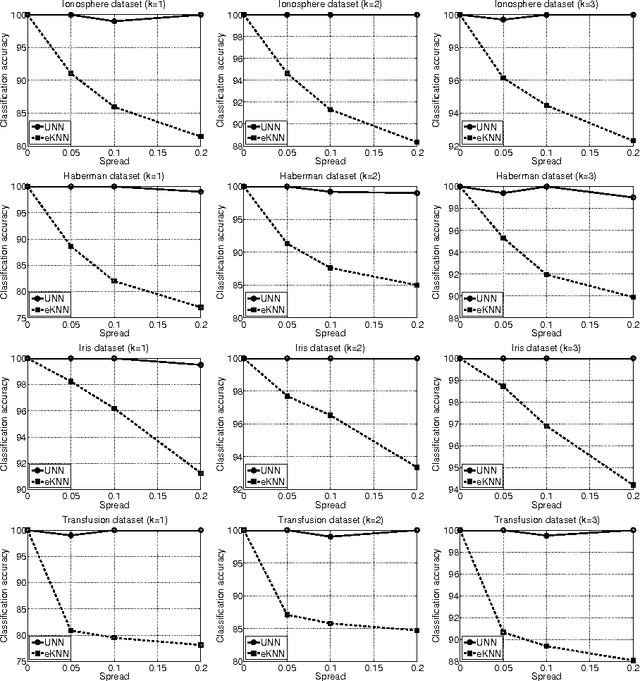
This work deals with the problem of classifying uncertain data. With this aim the Uncertain Nearest Neighbor (UNN) rule is here introduced, which represents the generalization of the deterministic nearest neighbor rule to the case in which uncertain objects are available. The UNN rule relies on the concept of nearest neighbor class, rather than on that of nearest neighbor object. The nearest neighbor class of a test object is the class that maximizes the probability of providing its nearest neighbor. It is provided evidence that the former concept is much more powerful than the latter one in the presence of uncertainty, in that it correctly models the right semantics of the nearest neighbor decision rule when applied to the uncertain scenario. An effective and efficient algorithm to perform uncertain nearest neighbor classification of a generic (un)certain test object is designed, based on properties that greatly reduce the temporal cost associated with nearest neighbor class probability computation. Experimental results are presented, showing that the UNN rule is effective and efficient in classifying uncertain data.