Gerald Pfeifer
Design and Implementation of Aggregate Functions in the DLV System
Feb 21, 2008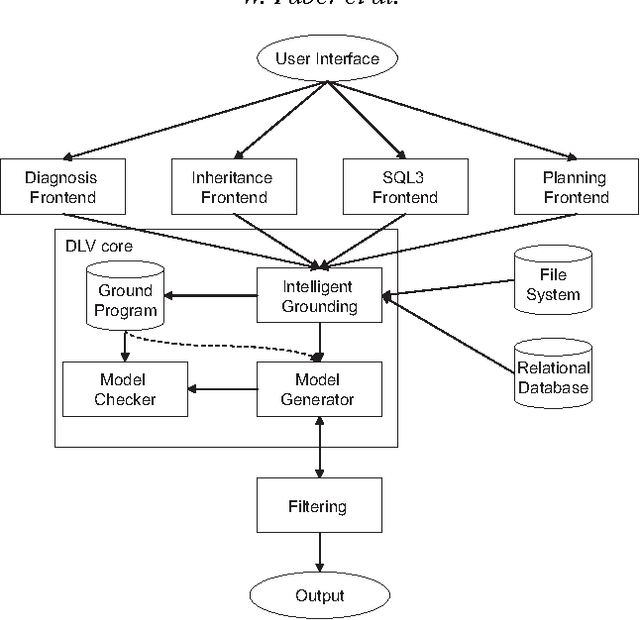
Abstract:Disjunctive Logic Programming (DLP) is a very expressive formalism: it allows for expressing every property of finite structures that is decidable in the complexity class SigmaP2 (= NP^NP). Despite this high expressiveness, there are some simple properties, often arising in real-world applications, which cannot be encoded in a simple and natural manner. Especially properties that require the use of arithmetic operators (like sum, times, or count) on a set or multiset of elements, which satisfy some conditions, cannot be naturally expressed in classic DLP. To overcome this deficiency, we extend DLP by aggregate functions in a conservative way. In particular, we avoid the introduction of constructs with disputed semantics, by requiring aggregates to be stratified. We formally define the semantics of the extended language (called DLP^A), and illustrate how it can be profitably used for representing knowledge. Furthermore, we analyze the computational complexity of DLP^A, showing that the addition of aggregates does not bring a higher cost in that respect. Finally, we provide an implementation of DLP^A in DLV -- a state-of-the-art DLP system -- and report on experiments which confirm the usefulness of the proposed extension also for the efficiency of computation.
The DLV System for Knowledge Representation and Reasoning
Sep 10, 2003


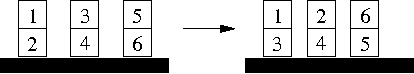
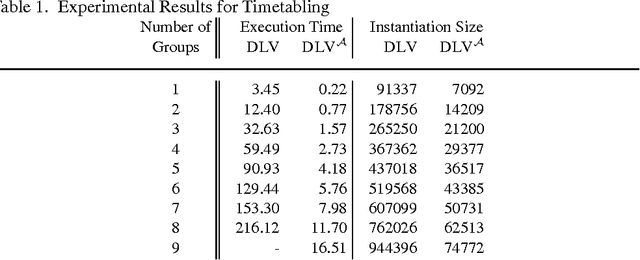
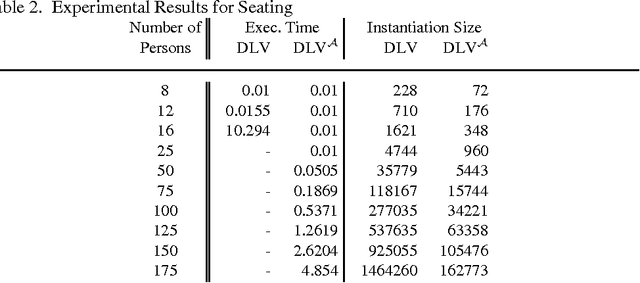
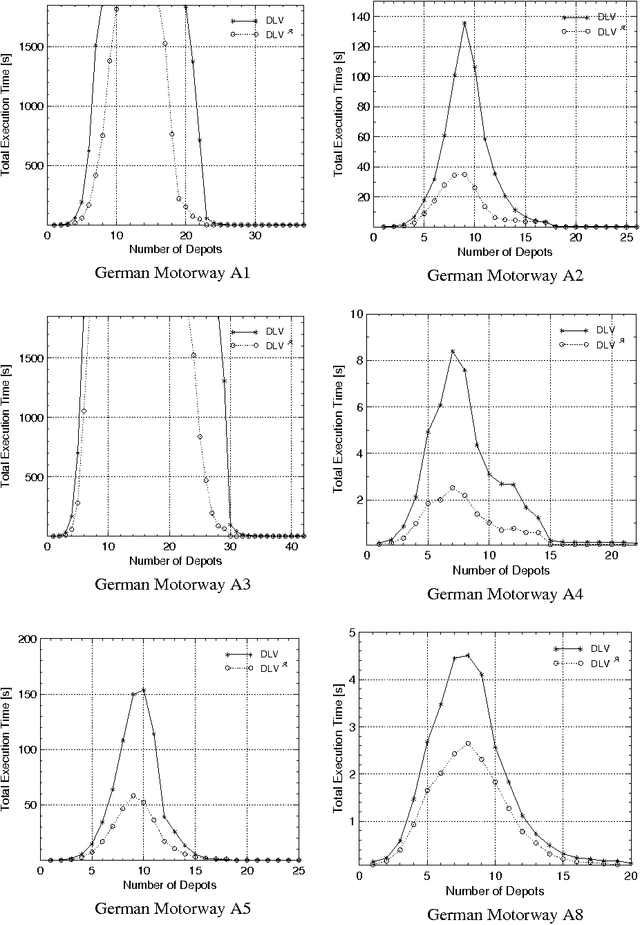
Abstract:This paper presents the DLV system, which is widely considered the state-of-the-art implementation of disjunctive logic programming, and addresses several aspects. As for problem solving, we provide a formal definition of its kernel language, function-free disjunctive logic programs (also known as disjunctive datalog), extended by weak constraints, which are a powerful tool to express optimization problems. We then illustrate the usage of DLV as a tool for knowledge representation and reasoning, describing a new declarative programming methodology which allows one to encode complex problems (up to $\Delta^P_3$-complete problems) in a declarative fashion. On the foundational side, we provide a detailed analysis of the computational complexity of the language of DLV, and by deriving new complexity results we chart a complete picture of the complexity of this language and important fragments thereof. Furthermore, we illustrate the general architecture of the DLV system which has been influenced by these results. As for applications, we overview application front-ends which have been developed on top of DLV to solve specific knowledge representation tasks, and we briefly describe the main international projects investigating the potential of the system for industrial exploitation. Finally, we report about thorough experimentation and benchmarking, which has been carried out to assess the efficiency of the system. The experimental results confirm the solidity of DLV and highlight its potential for emerging application areas like knowledge management and information integration.
* 56 pages, 9 figures, 6 tables
Computing Preferred Answer Sets by Meta-Interpretation in Answer Set Programming
Jan 16, 2002Abstract:Most recently, Answer Set Programming (ASP) is attracting interest as a new paradigm for problem solving. An important aspect which needs to be supported is the handling of preferences between rules, for which several approaches have been presented. In this paper, we consider the problem of implementing preference handling approaches by means of meta-interpreters in Answer Set Programming. In particular, we consider the preferred answer set approaches by Brewka and Eiter, by Delgrande, Schaub and Tompits, and by Wang, Zhou and Lin. We present suitable meta-interpreters for these semantics using DLV, which is an efficient engine for ASP. Moreover, we also present a meta-interpreter for the weakly preferred answer set approach by Brewka and Eiter, which uses the weak constraint feature of DLV as a tool for expressing and solving an underlying optimization problem. We also consider advanced meta-interpreters, which make use of graph-based characterizations and often allow for more efficient computations. Our approach shows the suitability of ASP in general and of DLV in particular for fast prototyping. This can be fruitfully exploited for experimenting with new languages and knowledge-representation formalisms.
* 34 pages, appeared as a Technical Report at KBS of the Vienna University of Technology, see http://www.kr.tuwien.ac.at/research/reports/
A Logic Programming Approach to Knowledge-State Planning: Semantics and Complexity
Dec 05, 2001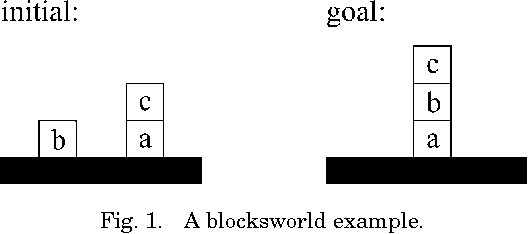


Abstract:We propose a new declarative planning language, called K, which is based on principles and methods of logic programming. In this language, transitions between states of knowledge can be described, rather than transitions between completely described states of the world, which makes the language well-suited for planning under incomplete knowledge. Furthermore, it enables the use of default principles in the planning process by supporting negation as failure. Nonetheless, K also supports the representation of transitions between states of the world (i.e., states of complete knowledge) as a special case, which shows that the language is very flexible. As we demonstrate on particular examples, the use of knowledge states may allow for a natural and compact problem representation. We then provide a thorough analysis of the computational complexity of K, and consider different planning problems, including standard planning and secure planning (also known as conformant planning) problems. We show that these problems have different complexities under various restrictions, ranging from NP to NEXPTIME in the propositional case. Our results form the theoretical basis for the DLV^K system, which implements the language K on top of the DLV logic programming system.
* 48 pages, appeared as a Technical Report at KBS of the Vienna University of Technology, see http://www.kr.tuwien.ac.at/research/reports/
DLV - A System for Declarative Problem Solving
Mar 08, 2000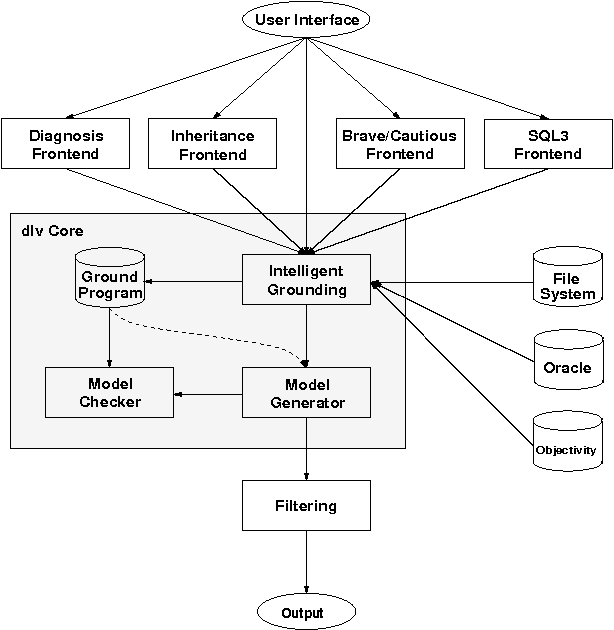
Abstract:DLV is an efficient logic programming and non-monotonic reasoning (LPNMR) system with advanced knowledge representation mechanisms and interfaces to classic relational database systems. Its core language is disjunctive datalog (function-free disjunctive logic programming) under the Answer Set Semantics with integrity constraints, both default and strong (or explicit) negation, and queries. Integer arithmetics and various built-in predicates are also supported. In addition DLV has several frontends, namely brave and cautious reasoning, abductive diagnosis, consistency-based diagnosis, a subset of SQL3, planning with action languages, and logic programming with inheritance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge