Giuseppe Ielpa
Design and Implementation of Aggregate Functions in the DLV System
Feb 21, 2008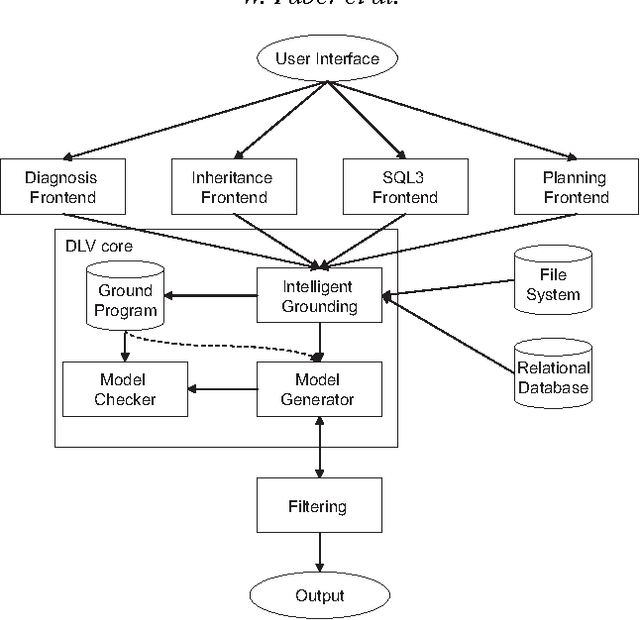
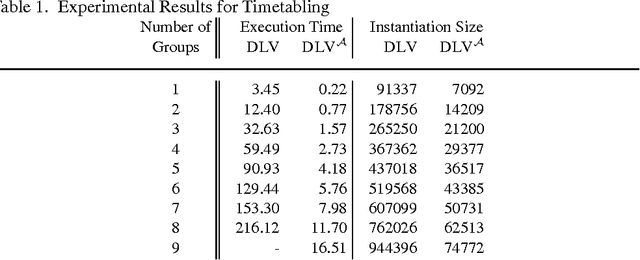
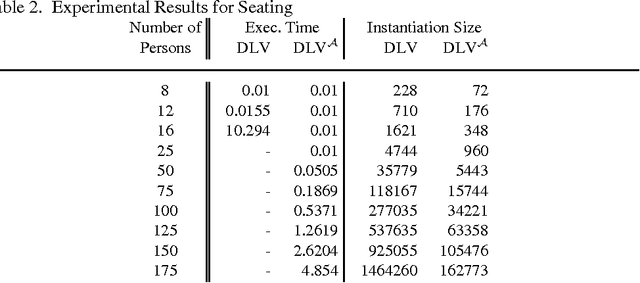
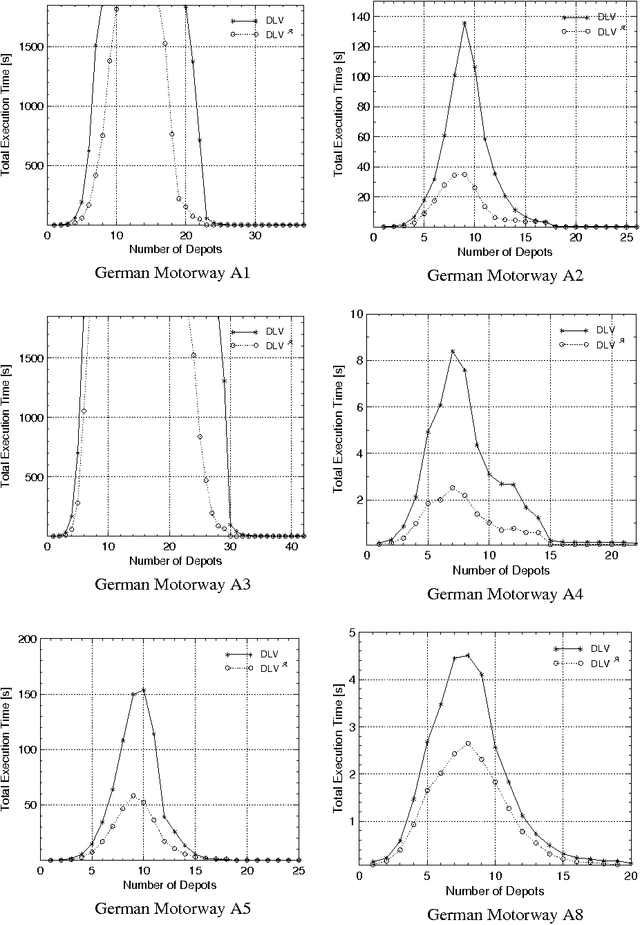
Abstract:Disjunctive Logic Programming (DLP) is a very expressive formalism: it allows for expressing every property of finite structures that is decidable in the complexity class SigmaP2 (= NP^NP). Despite this high expressiveness, there are some simple properties, often arising in real-world applications, which cannot be encoded in a simple and natural manner. Especially properties that require the use of arithmetic operators (like sum, times, or count) on a set or multiset of elements, which satisfy some conditions, cannot be naturally expressed in classic DLP. To overcome this deficiency, we extend DLP by aggregate functions in a conservative way. In particular, we avoid the introduction of constructs with disputed semantics, by requiring aggregates to be stratified. We formally define the semantics of the extended language (called DLP^A), and illustrate how it can be profitably used for representing knowledge. Furthermore, we analyze the computational complexity of DLP^A, showing that the addition of aggregates does not bring a higher cost in that respect. Finally, we provide an implementation of DLP^A in DLV -- a state-of-the-art DLP system -- and report on experiments which confirm the usefulness of the proposed extension also for the efficiency of computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge