Generating Random Logic Programs Using Constraint Programming
Paper and Code
Jun 02, 2020


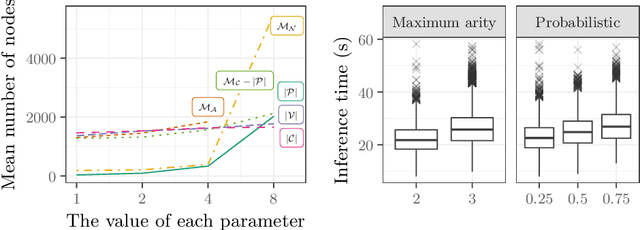
Testing algorithms across a wide range of problem instances is crucial to ensure the validity of any claim about one algorithm's superiority over another. However, when it comes to inference algorithms for probabilistic logic programs, experimental evaluations are limited to only a few programs. Existing methods to generate random logic programs are limited to propositional programs and often impose stringent syntactic restrictions. We present a novel approach to generating random logic programs and random probabilistic logic programs using constraint programming, introducing a new constraint to control the independence structure of the underlying probability distribution. We also provide a combinatorial argument for the correctness of the model, show how the model scales with parameter values, and use the model to compare probabilistic inference algorithms across a range of synthetic problems. Our model allows inference algorithm developers to evaluate and compare the algorithms across a wide range of instances, providing a detailed picture of their (comparative) strengths and weaknesses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge