Supratik Chakraborty
On Robustness of Linear Classifiers to Targeted Data Poisoning
Nov 16, 2025
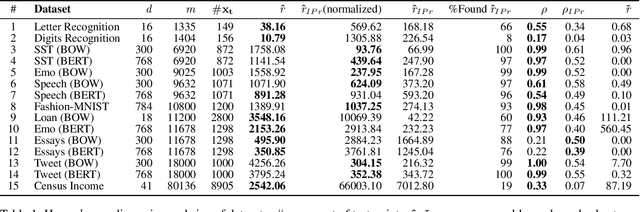
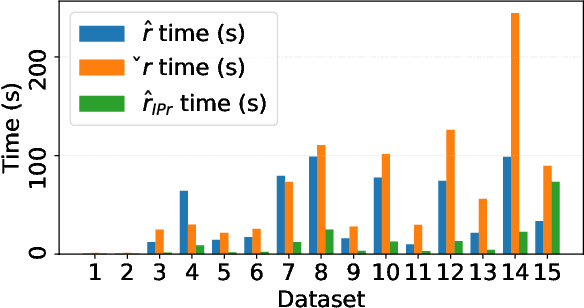
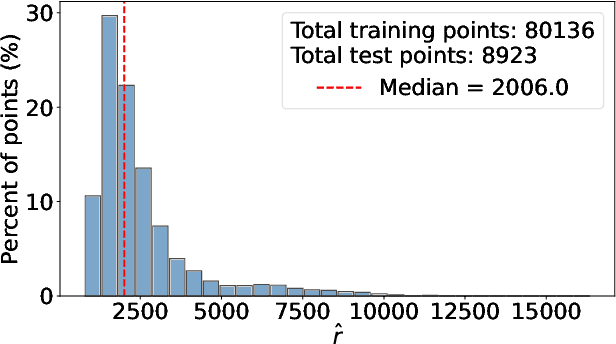
Abstract:Data poisoning is a training-time attack that undermines the trustworthiness of learned models. In a targeted data poisoning attack, an adversary manipulates the training dataset to alter the classification of a targeted test point. Given the typically large size of training dataset, manual detection of poisoning is difficult. An alternative is to automatically measure a dataset's robustness against such an attack, which is the focus of this paper. We consider a threat model wherein an adversary can only perturb the labels of the training dataset, with knowledge limited to the hypothesis space of the victim's model. In this setting, we prove that finding the robustness is an NP-Complete problem, even when hypotheses are linear classifiers. To overcome this, we present a technique that finds lower and upper bounds of robustness. Our implementation of the technique computes these bounds efficiently in practice for many publicly available datasets. We experimentally demonstrate the effectiveness of our approach. Specifically, a poisoning exceeding the identified robustness bounds significantly impacts test point classification. We are also able to compute these bounds in many more cases where state-of-the-art techniques fail.
Locally Pareto-Optimal Interpretations for Black-Box Machine Learning Models
Aug 21, 2025Abstract:Creating meaningful interpretations for black-box machine learning models involves balancing two often conflicting objectives: accuracy and explainability. Exploring the trade-off between these objectives is essential for developing trustworthy interpretations. While many techniques for multi-objective interpretation synthesis have been developed, they typically lack formal guarantees on the Pareto-optimality of the results. Methods that do provide such guarantees, on the other hand, often face severe scalability limitations when exploring the Pareto-optimal space. To address this, we develop a framework based on local optimality guarantees that enables more scalable synthesis of interpretations. Specifically, we consider the problem of synthesizing a set of Pareto-optimal interpretations with local optimality guarantees, within the immediate neighborhood of each solution. Our approach begins with a multi-objective learning or search technique, such as Multi-Objective Monte Carlo Tree Search, to generate a best-effort set of Pareto-optimal candidates with respect to accuracy and explainability. We then verify local optimality for each candidate as a Boolean satisfiability problem, which we solve using a SAT solver. We demonstrate the efficacy of our approach on a set of benchmarks, comparing it against previous methods for exploring the Pareto-optimal front of interpretations. In particular, we show that our approach yields interpretations that closely match those synthesized by methods offering global guarantees.
Presburger Functional Synthesis: Complexity and Tractable Normal Forms
Aug 10, 2025

Abstract:Given a relational specification between inputs and outputs as a logic formula, the problem of functional synthesis is to automatically synthesize a function from inputs to outputs satisfying the relation. Recently, a rich line of work has emerged tackling this problem for specifications in different theories, from Boolean to general first-order logic. In this paper, we launch an investigation of this problem for the theory of Presburger Arithmetic, that we call Presburger Functional Synthesis (PFnS). We show that PFnS can be solved in EXPTIME and provide a matching exponential lower bound. This is unlike the case for Boolean functional synthesis (BFnS), where only conditional exponential lower bounds are known. Further, we show that PFnS for one input and one output variable is as hard as BFnS in general. We then identify a special normal form, called PSyNF, for the specification formula that guarantees poly-time and poly-size solvability of PFnS. We prove several properties of PSyNF, including how to check and compile to this form, and conditions under which any other form that guarantees poly-time solvability of PFnS can be compiled in poly-time to PSyNF. Finally, we identify a syntactic normal form that is easier to check but is exponentially less succinct than PSyNF.
Counting Answer Sets of Disjunctive Answer Set Programs
Jul 15, 2025Abstract:Answer Set Programming (ASP) provides a powerful declarative paradigm for knowledge representation and reasoning. Recently, counting answer sets has emerged as an important computational problem with applications in probabilistic reasoning, network reliability analysis, and other domains. This has motivated significant research into designing efficient ASP counters. While substantial progress has been made for normal logic programs, the development of practical counters for disjunctive logic programs remains challenging. We present SharpASP-SR, a novel framework for counting answer sets of disjunctive logic programs based on subtractive reduction to projected propositional model counting. Our approach introduces an alternative characterization of answer sets that enables efficient reduction while ensuring that intermediate representations remain of polynomial size. This allows SharpASP-SR to leverage recent advances in projected model counting technology. Through extensive experimental evaluation on diverse benchmarks, we demonstrate that SharpASP-SR significantly outperforms existing counters on instances with large answer set counts. Building on these results, we develop a hybrid counting approach that combines enumeration techniques with SharpASP-SR to achieve state-of-the-art performance across the full spectrum of disjunctive programs.
Network Inversion of Binarised Neural Nets
Feb 19, 2024Abstract:While the deployment of neural networks, yielding impressive results, becomes more prevalent in various applications, their interpretability and understanding remain a critical challenge. Network inversion, a technique that aims to reconstruct the input space from the model's learned internal representations, plays a pivotal role in unraveling the black-box nature of input to output mappings in neural networks. In safety-critical scenarios, where model outputs may influence pivotal decisions, the integrity of the corresponding input space is paramount, necessitating the elimination of any extraneous "garbage" to ensure the trustworthiness of the network. Binarised Neural Networks (BNNs), characterized by binary weights and activations, offer computational efficiency and reduced memory requirements, making them suitable for resource-constrained environments. This paper introduces a novel approach to invert a trained BNN by encoding it into a CNF formula that captures the network's structure, allowing for both inference and inversion.
Exact ASP Counting with Compact Encodings
Dec 19, 2023


Abstract:Answer Set Programming (ASP) has emerged as a promising paradigm in knowledge representation and automated reasoning owing to its ability to model hard combinatorial problems from diverse domains in a natural way. Building on advances in propositional SAT solving, the past two decades have witnessed the emergence of well-engineered systems for solving the answer set satisfiability problem, i.e., finding models or answer sets for a given answer set program. In recent years, there has been growing interest in problems beyond satisfiability, such as model counting, in the context of ASP. Akin to the early days of propositional model counting, state-of-the-art exact answer set counters do not scale well beyond small instances. Exact ASP counters struggle with handling larger input formulas. The primary contribution of this paper is a new ASP counting framework, called sharpASP, which counts answer sets avoiding larger input formulas. This relies on an alternative way of defining answer sets that allows for the lifting of key techniques developed in the context of propositional model counting. Our extensive empirical analysis over 1470 benchmarks demonstrates significant performance gain over current state-of-the-art exact answer set counters. Specifically, by using sharpASP, we were able to solve 1062 benchmarks with PAR2 score of 3082 whereas using prior state-of-the-art, we could only solve 895 benchmarks with a PAR2 score of 4205, all other experimental conditions being the same.
Auditable Algorithms for Approximate Model Counting
Dec 19, 2023Abstract:Model counting, or counting the satisfying assignments of a Boolean formula, is a fundamental problem with diverse applications. Given #P-hardness of the problem, developing algorithms for approximate counting is an important research area. Building on the practical success of SAT-solvers, the focus has recently shifted from theory to practical implementations of approximate counting algorithms. This has brought to focus new challenges, such as the design of auditable approximate counters that not only provide an approximation of the model count, but also a certificate that a verifier with limited computational power can use to check if the count is indeed within the promised bounds of approximation. Towards generating certificates, we start by examining the best-known deterministic approximate counting algorithm that uses polynomially many calls to a $\Sigma_2^P$ oracle. We show that this can be audited via a $\Sigma_2^P$ oracle with the query constructed over $n^2 \log^2 n$ variables, where the original formula has $n$ variables. Since $n$ is often large, we ask if the count of variables in the certificate can be reduced -- a crucial question for potential implementation. We show that this is indeed possible with a tradeoff in the counting algorithm's complexity. Specifically, we develop new deterministic approximate counting algorithms that invoke a $\Sigma_3^P$ oracle, but can be certified using a $\Sigma_2^P$ oracle using certificates on far fewer variables: our final algorithm uses only $n \log n$ variables. Our study demonstrates that one can simplify auditing significantly if we allow the counting algorithm to access a slightly more powerful oracle. This shows for the first time how audit complexity can be traded for complexity of approximate counting.
Projected Model Counting: Beyond Independent Support
Oct 18, 2021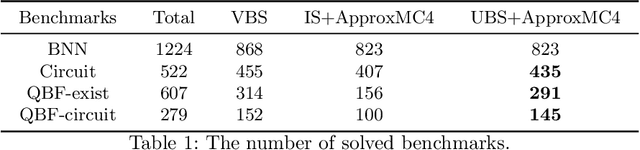

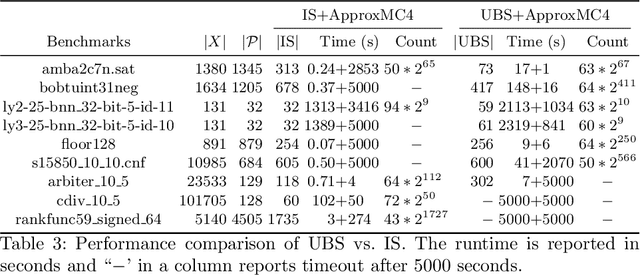
Abstract:The past decade has witnessed a surge of interest in practical techniques for projected model counting. Despite significant advancements, however, performance scaling remains the Achilles' heel of this field. A key idea used in modern counters is to count models projected on an \emph{independent support} that is often a small subset of the projection set, i.e. original set of variables on which we wanted to project. While this idea has been effective in scaling performance, the question of whether it can benefit to count models projected on variables beyond the projection set, has not been explored. In this paper, we study this question and show that contrary to intuition, it can be beneficial to project on variables beyond the projection set. In applications such as verification of binarized neural networks, quantification of information flow, reliability of power grids etc., a good upper bound of the projected model count often suffices. We show that in several such cases, we can identify a set of variables, called upper bound support (UBS), that is not necessarily a subset of the projection set, and yet counting models projected on UBS guarantees an upper bound of the true projected model count. Theoretically, a UBS can be exponentially smaller than the smallest independent support. Our experiments show that even otherwise, UBS-based projected counting can be more efficient than independent support-based projected counting, while yielding bounds of very high quality. Based on extensive experiments, we find that UBS-based projected counting can solve many problem instances that are beyond the reach of a state-of-the-art independent support-based projected model counter.
Synthesizing Pareto-Optimal Interpretations for Black-Box Models
Aug 16, 2021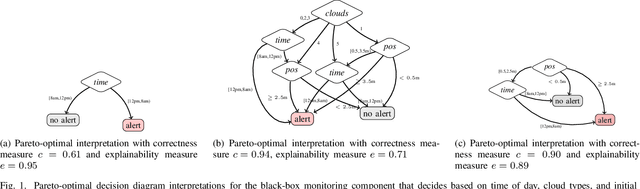
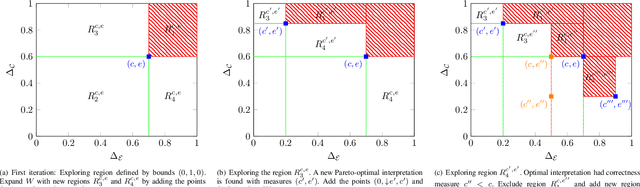
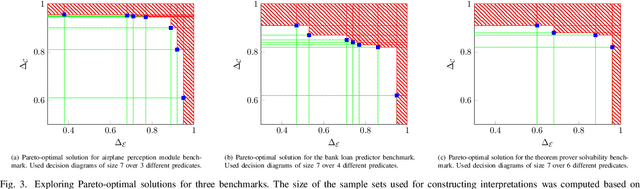
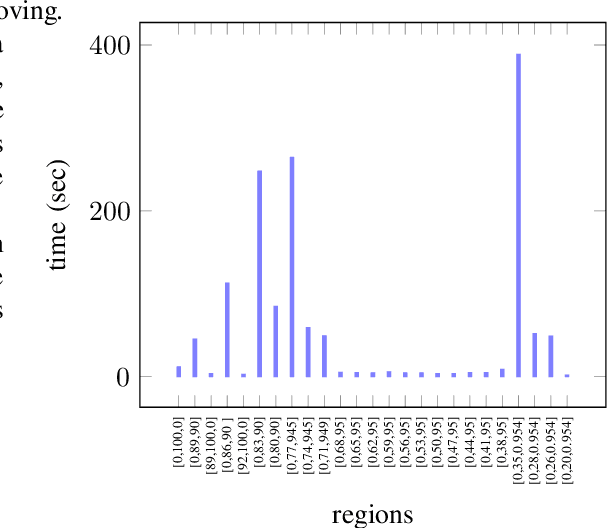
Abstract:We present a new multi-objective optimization approach for synthesizing interpretations that "explain" the behavior of black-box machine learning models. Constructing human-understandable interpretations for black-box models often requires balancing conflicting objectives. A simple interpretation may be easier to understand for humans while being less precise in its predictions vis-a-vis a complex interpretation. Existing methods for synthesizing interpretations use a single objective function and are often optimized for a single class of interpretations. In contrast, we provide a more general and multi-objective synthesis framework that allows users to choose (1) the class of syntactic templates from which an interpretation should be synthesized, and (2) quantitative measures on both the correctness and explainability of an interpretation. For a given black-box, our approach yields a set of Pareto-optimal interpretations with respect to the correctness and explainability measures. We show that the underlying multi-objective optimization problem can be solved via a reduction to quantitative constraint solving, such as weighted maximum satisfiability. To demonstrate the benefits of our approach, we have applied it to synthesize interpretations for black-box neural-network classifiers. Our experiments show that there often exists a rich and varied set of choices for interpretations that are missed by existing approaches.
A Normal Form Characterization for Efficient Boolean Skolem Function Synthesis
Apr 29, 2021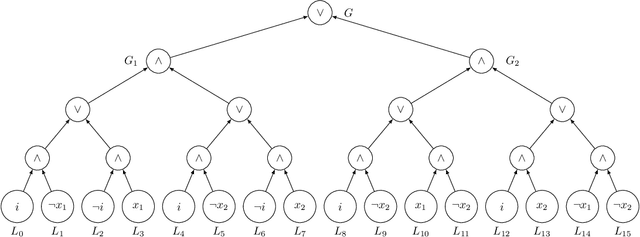
Abstract:Boolean Skolem function synthesis concerns synthesizing outputs as Boolean functions of inputs such that a relational specification between inputs and outputs is satisfied. This problem, also known as Boolean functional synthesis, has several applications, including design of safe controllers for autonomous systems, certified QBF solving, cryptanalysis etc. Recently, complexity theoretic hardness results have been shown for the problem, although several algorithms proposed in the literature are known to work well in practice. This dichotomy between theoretical hardness and practical efficacy has motivated the research into normal forms or representations of input specifications that permit efficient synthesis, thus explaining perhaps the efficacy of these algorithms. In this paper we go one step beyond this and ask if there exists a normal form representation that can in fact precisely characterize "efficient" synthesis. We present a normal form called SAUNF that precisely characterizes tractable synthesis in the following sense: a specification is polynomial time synthesizable iff it can be compiled to SAUNF in polynomial time. Additionally, a specification admits a polynomial-sized functional solution iff there exists a semantically equivalent polynomial-sized SAUNF representation. SAUNF is exponentially more succinct than well-established normal forms like BDDs and DNNFs, used in the context of AI problems, and strictly subsumes other more recently proposed forms like SynNNF. It enjoys compositional properties that are similar to those of DNNF. Thus, SAUNF provides the right trade-off in knowledge representation for Boolean functional synthesis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge