Preey Shah
S4ND: Modeling Images and Videos as Multidimensional Signals Using State Spaces
Oct 14, 2022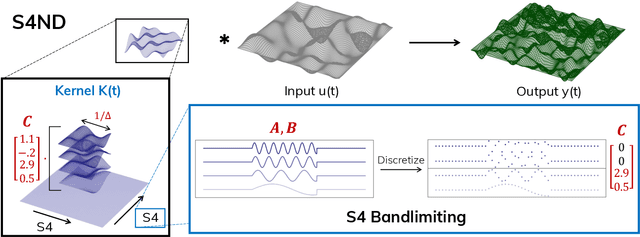
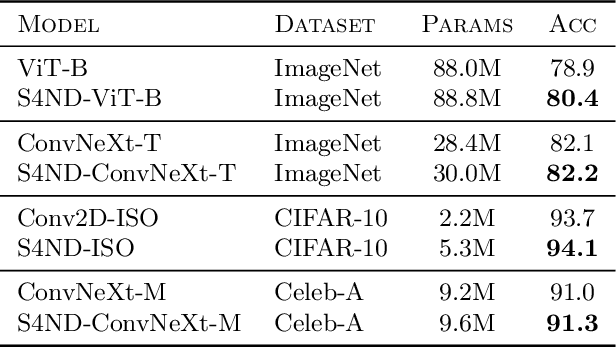
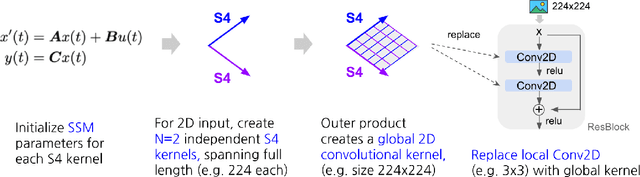
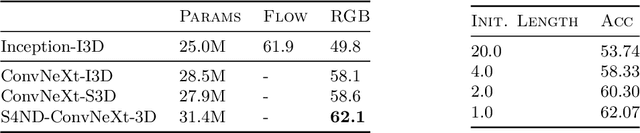
Abstract:Visual data such as images and videos are typically modeled as discretizations of inherently continuous, multidimensional signals. Existing continuous-signal models attempt to exploit this fact by modeling the underlying signals of visual (e.g., image) data directly. However, these models have not yet been able to achieve competitive performance on practical vision tasks such as large-scale image and video classification. Building on a recent line of work on deep state space models (SSMs), we propose S4ND, a new multidimensional SSM layer that extends the continuous-signal modeling ability of SSMs to multidimensional data including images and videos. We show that S4ND can model large-scale visual data in $1$D, $2$D, and $3$D as continuous multidimensional signals and demonstrates strong performance by simply swapping Conv2D and self-attention layers with S4ND layers in existing state-of-the-art models. On ImageNet-1k, S4ND exceeds the performance of a Vision Transformer baseline by $1.5\%$ when training with a $1$D sequence of patches, and matches ConvNeXt when modeling images in $2$D. For videos, S4ND improves on an inflated $3$D ConvNeXt in activity classification on HMDB-51 by $4\%$. S4ND implicitly learns global, continuous convolutional kernels that are resolution invariant by construction, providing an inductive bias that enables generalization across multiple resolutions. By developing a simple bandlimiting modification to S4 to overcome aliasing, S4ND achieves strong zero-shot (unseen at training time) resolution performance, outperforming a baseline Conv2D by $40\%$ on CIFAR-10 when trained on $8 \times 8$ and tested on $32 \times 32$ images. When trained with progressive resizing, S4ND comes within $\sim 1\%$ of a high-resolution model while training $22\%$ faster.
A Normal Form Characterization for Efficient Boolean Skolem Function Synthesis
Apr 29, 2021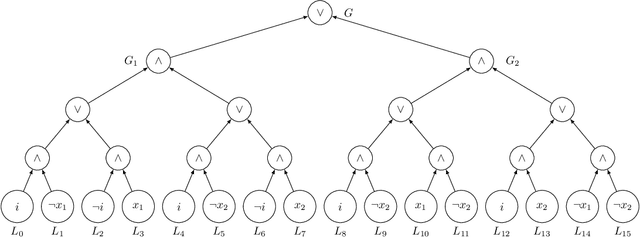
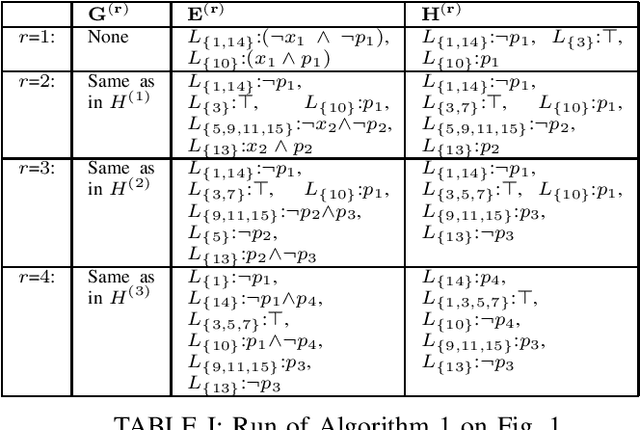
Abstract:Boolean Skolem function synthesis concerns synthesizing outputs as Boolean functions of inputs such that a relational specification between inputs and outputs is satisfied. This problem, also known as Boolean functional synthesis, has several applications, including design of safe controllers for autonomous systems, certified QBF solving, cryptanalysis etc. Recently, complexity theoretic hardness results have been shown for the problem, although several algorithms proposed in the literature are known to work well in practice. This dichotomy between theoretical hardness and practical efficacy has motivated the research into normal forms or representations of input specifications that permit efficient synthesis, thus explaining perhaps the efficacy of these algorithms. In this paper we go one step beyond this and ask if there exists a normal form representation that can in fact precisely characterize "efficient" synthesis. We present a normal form called SAUNF that precisely characterizes tractable synthesis in the following sense: a specification is polynomial time synthesizable iff it can be compiled to SAUNF in polynomial time. Additionally, a specification admits a polynomial-sized functional solution iff there exists a semantically equivalent polynomial-sized SAUNF representation. SAUNF is exponentially more succinct than well-established normal forms like BDDs and DNNFs, used in the context of AI problems, and strictly subsumes other more recently proposed forms like SynNNF. It enjoys compositional properties that are similar to those of DNNF. Thus, SAUNF provides the right trade-off in knowledge representation for Boolean functional synthesis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge