Data-Aware and Scalable Sensitivity Analysis for Decision Tree Ensembles

Decision tree ensembles are widely used in critical domains, making robustness and sensitivity analysis essential to their trustworthiness. We study the feature sensitivity problem, which asks whether an ensemble is sensitive to a specified subset of features -- such as protected attributes -- whose manipulation can alter model predictions. Existing approaches often yield examples of sensitivity that lie far from the training distribution, limiting their interpretability and practical value. We propose a data-aware sensitivity framework that constrains the sensitive examples to remain close to the dataset, thereby producing realistic and interpretable evidence of model weaknesses. To this end, we develop novel techniques for data-aware search using a combination of mixed-integer linear programming (MILP) and satisfiability modulo theories (SMT) encodings. Our contributions are fourfold. First, we strengthen the NP-hardness result for sensitivity verification, showing it holds even for trees of depth 1. Second, we develop MILP-optimizations that significantly speed up sensitivity verification for single ensembles and for the first time can also handle multiclass tree ensembles. Third, we introduce a data-aware framework generating realistic examples close to the training distribution. Finally, we conduct an extensive experimental evaluation on large tree ensembles, demonstrating scalability to ensembles with up to 800 trees of depth 8, achieving substantial improvements over the state of the art. This framework provides a practical foundation for analyzing the reliability and fairness of tree-based models in high-stakes applications.

Verifying rich robustness properties for neural networks

Robustness is a important problem in AI alignment and safety, with models such as neural networks being increasingly used in safety-critical systems. In the last decade, a large body of work has emerged on local robustness, i.e., checking if the decision of a neural network remains unchanged when the input is slightly perturbed. However, many of these approaches require specialized encoding and often ignore the confidence of a neural network on its output. In this paper, our goal is to build a generalized framework to specify and verify variants of robustness in neural network verification. We propose a specification framework using a simple grammar, which is flexible enough to capture most existing variants. This allows us to introduce new variants of robustness that take into account the confidence of the neural network in its outputs. Next, we develop a novel and powerful unified technique to verify all such variants in a homogeneous way, viz., by adding a few additional layers to the neural network. This enables us to use any state-of-the-art neural network verification tool, without having to tinker with the encoding within, while incurring an approximation error that we show is bounded. We perform an extensive experimental evaluation over a large suite of 8870 benchmarks having 138M parameters in a largest network, and show that we are able to capture a wide set of robustness variants and outperform direct encoding approaches by a significant margin.

Presburger Functional Synthesis: Complexity and Tractable Normal Forms

Given a relational specification between inputs and outputs as a logic formula, the problem of functional synthesis is to automatically synthesize a function from inputs to outputs satisfying the relation. Recently, a rich line of work has emerged tackling this problem for specifications in different theories, from Boolean to general first-order logic. In this paper, we launch an investigation of this problem for the theory of Presburger Arithmetic, that we call Presburger Functional Synthesis (PFnS). We show that PFnS can be solved in EXPTIME and provide a matching exponential lower bound. This is unlike the case for Boolean functional synthesis (BFnS), where only conditional exponential lower bounds are known. Further, we show that PFnS for one input and one output variable is as hard as BFnS in general. We then identify a special normal form, called PSyNF, for the specification formula that guarantees poly-time and poly-size solvability of PFnS. We prove several properties of PSyNF, including how to check and compile to this form, and conditions under which any other form that guarantees poly-time solvability of PFnS can be compiled in poly-time to PSyNF. Finally, we identify a syntactic normal form that is easier to check but is exponentially less succinct than PSyNF.

Certified Policy Verification and Synthesis for MDPs under Distributional Reach-avoidance Properties

Markov Decision Processes (MDPs) are a classical model for decision making in the presence of uncertainty. Often they are viewed as state transformers with planning objectives defined with respect to paths over MDP states. An increasingly popular alternative is to view them as distribution transformers, giving rise to a sequence of probability distributions over MDP states. For instance, reachability and safety properties in modeling robot swarms or chemical reaction networks are naturally defined in terms of probability distributions over states. Verifying such distributional properties is known to be hard and often beyond the reach of classical state-based verification techniques. In this work, we consider the problems of certified policy (i.e. controller) verification and synthesis in MDPs under distributional reach-avoidance specifications. By certified we mean that, along with a policy, we also aim to synthesize a (checkable) certificate ensuring that the MDP indeed satisfies the property. Thus, given the target set of distributions and an unsafe set of distributions over MDP states, our goal is to either synthesize a certificate for a given policy or synthesize a policy along with a certificate, proving that the target distribution can be reached while avoiding unsafe distributions. To solve this problem, we introduce the novel notion of distributional reach-avoid certificates and present automated procedures for (1) synthesizing a certificate for a given policy, and (2) synthesizing a policy together with the certificate, both providing formal guarantees on certificate correctness. Our experimental evaluation demonstrates the ability of our method to solve several non-trivial examples, including a multi-agent robot-swarm model, to synthesize certified policies and to certify existing policies.

Auditable Algorithms for Approximate Model Counting

Model counting, or counting the satisfying assignments of a Boolean formula, is a fundamental problem with diverse applications. Given #P-hardness of the problem, developing algorithms for approximate counting is an important research area. Building on the practical success of SAT-solvers, the focus has recently shifted from theory to practical implementations of approximate counting algorithms. This has brought to focus new challenges, such as the design of auditable approximate counters that not only provide an approximation of the model count, but also a certificate that a verifier with limited computational power can use to check if the count is indeed within the promised bounds of approximation. Towards generating certificates, we start by examining the best-known deterministic approximate counting algorithm that uses polynomially many calls to a $\Sigma_2^P$ oracle. We show that this can be audited via a $\Sigma_2^P$ oracle with the query constructed over $n^2 \log^2 n$ variables, where the original formula has $n$ variables. Since $n$ is often large, we ask if the count of variables in the certificate can be reduced -- a crucial question for potential implementation. We show that this is indeed possible with a tradeoff in the counting algorithm's complexity. Specifically, we develop new deterministic approximate counting algorithms that invoke a $\Sigma_3^P$ oracle, but can be certified using a $\Sigma_2^P$ oracle using certificates on far fewer variables: our final algorithm uses only $n \log n$ variables. Our study demonstrates that one can simplify auditing significantly if we allow the counting algorithm to access a slightly more powerful oracle. This shows for the first time how audit complexity can be traded for complexity of approximate counting.

Synthesizing Pareto-Optimal Interpretations for Black-Box Models

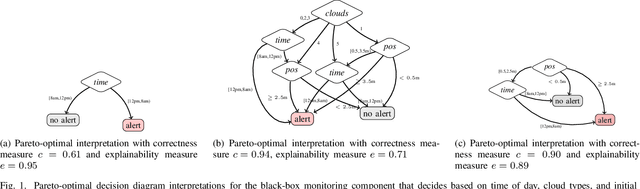
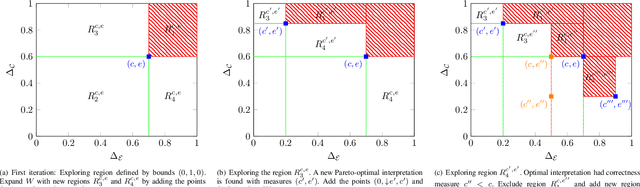
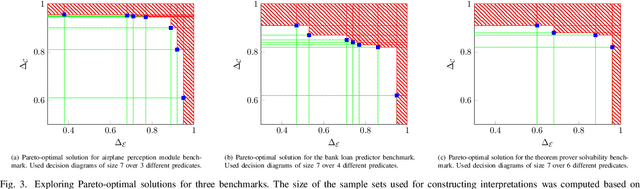
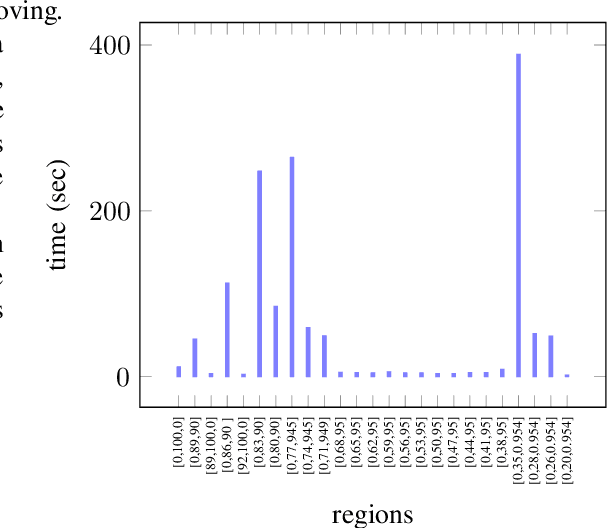
We present a new multi-objective optimization approach for synthesizing interpretations that "explain" the behavior of black-box machine learning models. Constructing human-understandable interpretations for black-box models often requires balancing conflicting objectives. A simple interpretation may be easier to understand for humans while being less precise in its predictions vis-a-vis a complex interpretation. Existing methods for synthesizing interpretations use a single objective function and are often optimized for a single class of interpretations. In contrast, we provide a more general and multi-objective synthesis framework that allows users to choose (1) the class of syntactic templates from which an interpretation should be synthesized, and (2) quantitative measures on both the correctness and explainability of an interpretation. For a given black-box, our approach yields a set of Pareto-optimal interpretations with respect to the correctness and explainability measures. We show that the underlying multi-objective optimization problem can be solved via a reduction to quantitative constraint solving, such as weighted maximum satisfiability. To demonstrate the benefits of our approach, we have applied it to synthesize interpretations for black-box neural-network classifiers. Our experiments show that there often exists a rich and varied set of choices for interpretations that are missed by existing approaches.

A Normal Form Characterization for Efficient Boolean Skolem Function Synthesis

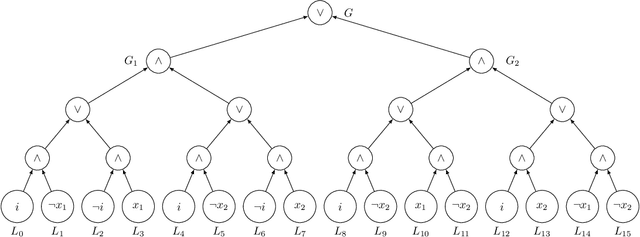
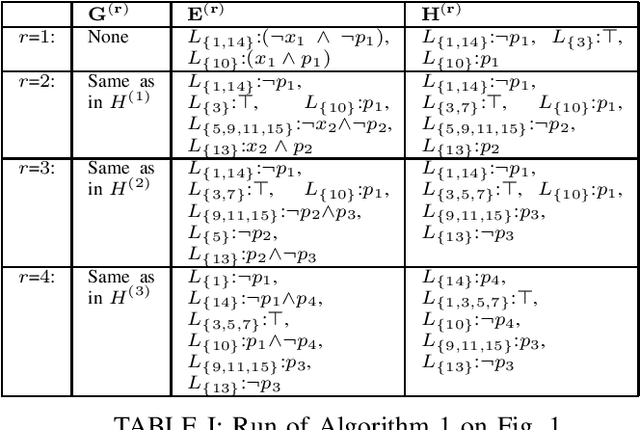
Boolean Skolem function synthesis concerns synthesizing outputs as Boolean functions of inputs such that a relational specification between inputs and outputs is satisfied. This problem, also known as Boolean functional synthesis, has several applications, including design of safe controllers for autonomous systems, certified QBF solving, cryptanalysis etc. Recently, complexity theoretic hardness results have been shown for the problem, although several algorithms proposed in the literature are known to work well in practice. This dichotomy between theoretical hardness and practical efficacy has motivated the research into normal forms or representations of input specifications that permit efficient synthesis, thus explaining perhaps the efficacy of these algorithms. In this paper we go one step beyond this and ask if there exists a normal form representation that can in fact precisely characterize "efficient" synthesis. We present a normal form called SAUNF that precisely characterizes tractable synthesis in the following sense: a specification is polynomial time synthesizable iff it can be compiled to SAUNF in polynomial time. Additionally, a specification admits a polynomial-sized functional solution iff there exists a semantically equivalent polynomial-sized SAUNF representation. SAUNF is exponentially more succinct than well-established normal forms like BDDs and DNNFs, used in the context of AI problems, and strictly subsumes other more recently proposed forms like SynNNF. It enjoys compositional properties that are similar to those of DNNF. Thus, SAUNF provides the right trade-off in knowledge representation for Boolean functional synthesis.

Sparse Hashing for Scalable Approximate Model Counting: Theory and Practice

Given a CNF formula F on n variables, the problem of model counting or #SAT is to compute the number of satisfying assignments of F . Model counting is a fundamental but hard problem in computer science with varied applications. Recent years have witnessed a surge of effort towards developing efficient algorithmic techniques that combine the classical 2-universal hashing with the remarkable progress in SAT solving over the past decade. These techniques augment the CNF formula F with random XOR constraints and invoke an NP oracle repeatedly on the resultant CNF-XOR formulas. In practice, calls to the NP oracle calls are replaced a SAT solver whose runtime performance is adversely affected by size of XOR constraints. The standard construction of 2-universal hash functions chooses every variable with probability p = 1/2 leading to XOR constraints of size n/2 in expectation. Consequently, the challenge is to design sparse hash functions where variables can be chosen with smaller probability and lead to smaller sized XOR constraints. In this paper, we address this challenge from theoretical and practical perspectives. First, we formalize a relaxation of universal hashing, called concentrated hashing and establish a novel and beautiful connection between concentration measures of these hash functions and isoperimetric inequalities on boolean hypercubes. This allows us to obtain (log m) tight bounds on variance and dispersion index and show that p = O( log(m)/m ) suffices for design of sparse hash functions from {0, 1}^n to {0, 1}^m. We then use sparse hash functions belonging to this concentrated hash family to develop new approximate counting algorithms. A comprehensive experimental evaluation of our algorithm on 1893 benchmarks demonstrates that usage of sparse hash functions can lead to significant speedups.