Neural Control and Certificate Repair via Runtime Monitoring

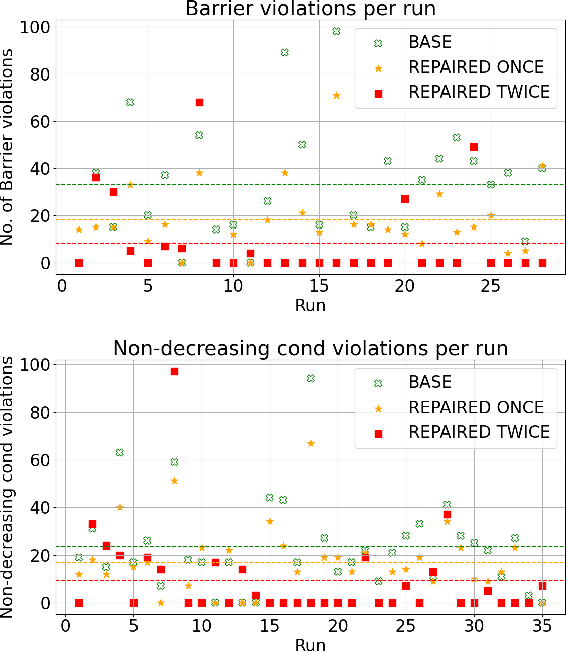
Learning-based methods provide a promising approach to solving highly non-linear control tasks that are often challenging for classical control methods. To ensure the satisfaction of a safety property, learning-based methods jointly learn a control policy together with a certificate function for the property. Popular examples include barrier functions for safety and Lyapunov functions for asymptotic stability. While there has been significant progress on learning-based control with certificate functions in the white-box setting, where the correctness of the certificate function can be formally verified, there has been little work on ensuring their reliability in the black-box setting where the system dynamics are unknown. In this work, we consider the problems of certifying and repairing neural network control policies and certificate functions in the black-box setting. We propose a novel framework that utilizes runtime monitoring to detect system behaviors that violate the property of interest under some initially trained neural network policy and certificate. These violating behaviors are used to extract new training data, that is used to re-train the neural network policy and the certificate function and to ultimately repair them. We demonstrate the effectiveness of our approach empirically by using it to repair and to boost the safety rate of neural network policies learned by a state-of-the-art method for learning-based control on two autonomous system control tasks.

Certified Policy Verification and Synthesis for MDPs under Distributional Reach-avoidance Properties

Markov Decision Processes (MDPs) are a classical model for decision making in the presence of uncertainty. Often they are viewed as state transformers with planning objectives defined with respect to paths over MDP states. An increasingly popular alternative is to view them as distribution transformers, giving rise to a sequence of probability distributions over MDP states. For instance, reachability and safety properties in modeling robot swarms or chemical reaction networks are naturally defined in terms of probability distributions over states. Verifying such distributional properties is known to be hard and often beyond the reach of classical state-based verification techniques. In this work, we consider the problems of certified policy (i.e. controller) verification and synthesis in MDPs under distributional reach-avoidance specifications. By certified we mean that, along with a policy, we also aim to synthesize a (checkable) certificate ensuring that the MDP indeed satisfies the property. Thus, given the target set of distributions and an unsafe set of distributions over MDP states, our goal is to either synthesize a certificate for a given policy or synthesize a policy along with a certificate, proving that the target distribution can be reached while avoiding unsafe distributions. To solve this problem, we introduce the novel notion of distributional reach-avoid certificates and present automated procedures for (1) synthesizing a certificate for a given policy, and (2) synthesizing a policy together with the certificate, both providing formal guarantees on certificate correctness. Our experimental evaluation demonstrates the ability of our method to solve several non-trivial examples, including a multi-agent robot-swarm model, to synthesize certified policies and to certify existing policies.

Solving Long-run Average Reward Robust MDPs via Stochastic Games

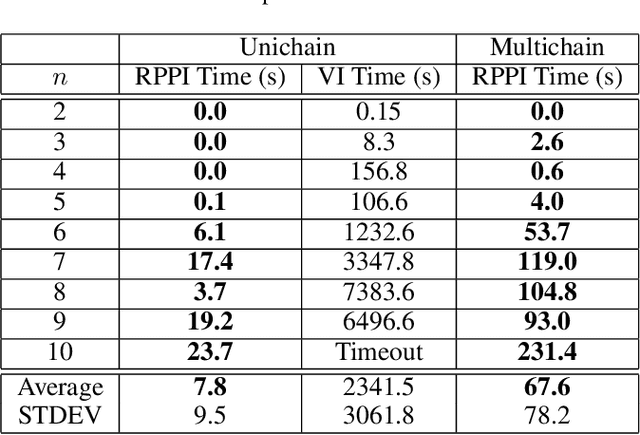
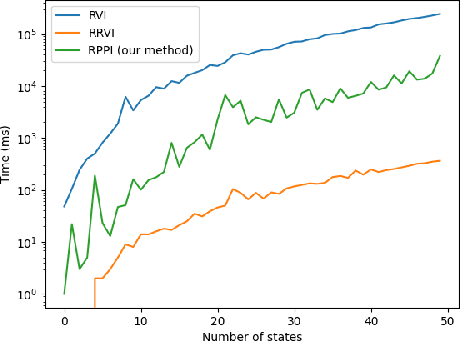
Markov decision processes (MDPs) provide a standard framework for sequential decision making under uncertainty. However, transition probabilities in MDPs are often estimated from data and MDPs do not take data uncertainty into account. Robust Markov decision processes (RMDPs) address this shortcoming of MDPs by assigning to each transition an uncertainty set rather than a single probability value. The goal of solving RMDPs is then to find a policy which maximizes the worst-case performance over the uncertainty sets. In this work, we consider polytopic RMDPs in which all uncertainty sets are polytopes and study the problem of solving long-run average reward polytopic RMDPs. Our focus is on computational complexity aspects and efficient algorithms. We present a novel perspective on this problem and show that it can be reduced to solving long-run average reward turn-based stochastic games with finite state and action spaces. This reduction allows us to derive several important consequences that were hitherto not known to hold for polytopic RMDPs. First, we derive new computational complexity bounds for solving long-run average reward polytopic RMDPs, showing for the first time that the threshold decision problem for them is in NP coNP and that they admit a randomized algorithm with sub-exponential expected runtime. Second, we present Robust Polytopic Policy Iteration (RPPI), a novel policy iteration algorithm for solving long-run average reward polytopic RMDPs. Our experimental evaluation shows that RPPI is much more efficient in solving long-run average reward polytopic RMDPs compared to state-of-the-art methods based on value iteration.

Compositional Policy Learning in Stochastic Control Systems with Formal Guarantees

Reinforcement learning has shown promising results in learning neural network policies for complicated control tasks. However, the lack of formal guarantees about the behavior of such policies remains an impediment to their deployment. We propose a novel method for learning a composition of neural network policies in stochastic environments, along with a formal certificate which guarantees that a specification over the policy's behavior is satisfied with the desired probability. Unlike prior work on verifiable RL, our approach leverages the compositional nature of logical specifications provided in SpectRL, to learn over graphs of probabilistic reach-avoid specifications. The formal guarantees are provided by learning neural network policies together with reach-avoid supermartingales (RASM) for the graph's sub-tasks and then composing them into a global policy. We also derive a tighter lower bound compared to previous work on the probability of reach-avoidance implied by a RASM, which is required to find a compositional policy with an acceptable probabilistic threshold for complex tasks with multiple edge policies. We implement a prototype of our approach and evaluate it on a Stochastic Nine Rooms environment.

Reachability Poorman Discrete-Bidding Games

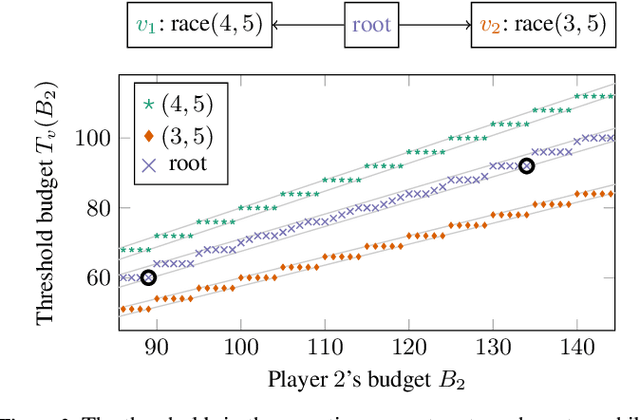
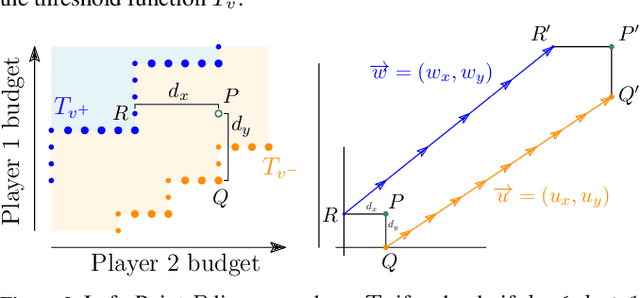
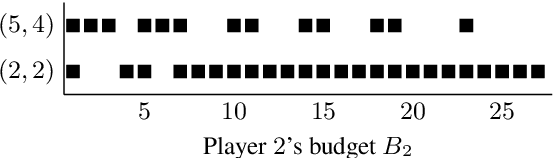
We consider {\em bidding games}, a class of two-player zero-sum {\em graph games}. The game proceeds as follows. Both players have bounded budgets. A token is placed on a vertex of a graph, in each turn the players simultaneously submit bids, and the higher bidder moves the token, where we break bidding ties in favor of Player 1. Player 1 wins the game iff the token visits a designated target vertex. We consider, for the first time, {\em poorman discrete-bidding} in which the granularity of the bids is restricted and the higher bid is paid to the bank. Previous work either did not impose granularity restrictions or considered {\em Richman} bidding (bids are paid to the opponent). While the latter mechanisms are technically more accessible, the former is more appealing from a practical standpoint. Our study focuses on {\em threshold budgets}, which is the necessary and sufficient initial budget required for Player 1 to ensure winning against a given Player 2 budget. We first show existence of thresholds. In DAGs, we show that threshold budgets can be approximated with error bounds by thresholds under continuous-bidding and that they exhibit a periodic behavior. We identify closed-form solutions in special cases. We implement and experiment with an algorithm to find threshold budgets.

Quantization-aware Interval Bound Propagation for Training Certifiably Robust Quantized Neural Networks

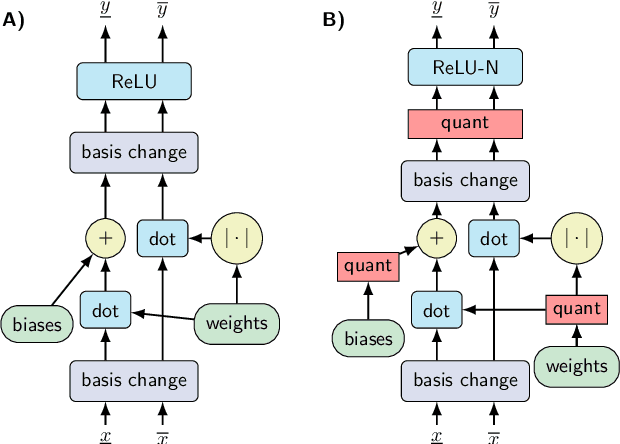
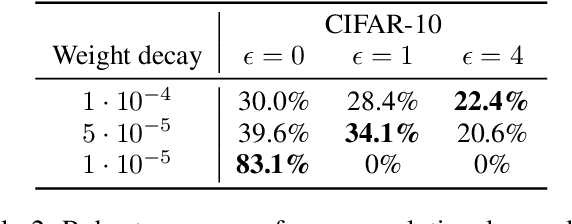
We study the problem of training and certifying adversarially robust quantized neural networks (QNNs). Quantization is a technique for making neural networks more efficient by running them using low-bit integer arithmetic and is therefore commonly adopted in industry. Recent work has shown that floating-point neural networks that have been verified to be robust can become vulnerable to adversarial attacks after quantization, and certification of the quantized representation is necessary to guarantee robustness. In this work, we present quantization-aware interval bound propagation (QA-IBP), a novel method for training robust QNNs. Inspired by advances in robust learning of non-quantized networks, our training algorithm computes the gradient of an abstract representation of the actual network. Unlike existing approaches, our method can handle the discrete semantics of QNNs. Based on QA-IBP, we also develop a complete verification procedure for verifying the adversarial robustness of QNNs, which is guaranteed to terminate and produce a correct answer. Compared to existing approaches, the key advantage of our verification procedure is that it runs entirely on GPU or other accelerator devices. We demonstrate experimentally that our approach significantly outperforms existing methods and establish the new state-of-the-art for training and certifying the robustness of QNNs.

Learning Control Policies for Stochastic Systems with Reach-avoid Guarantees

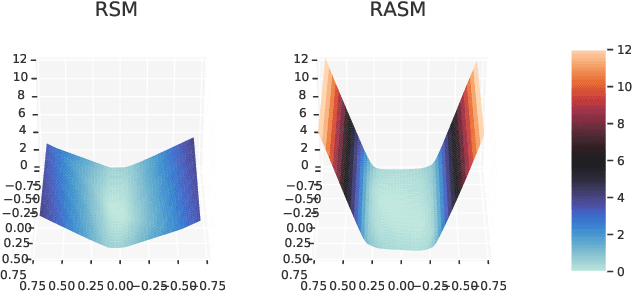
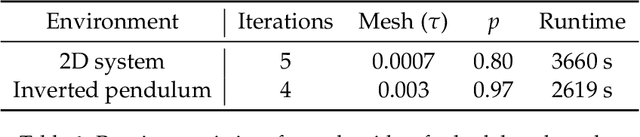
We study the problem of learning controllers for discrete-time non-linear stochastic dynamical systems with formal reach-avoid guarantees. This work presents the first method for providing formal reach-avoid guarantees, which combine and generalize stability and safety guarantees, with a tolerable probability threshold $p\in[0,1]$ over the infinite time horizon. Our method leverages advances in machine learning literature and it represents formal certificates as neural networks. In particular, we learn a certificate in the form of a reach-avoid supermartingale (RASM), a novel notion that we introduce in this work. Our RASMs provide reachability and avoidance guarantees by imposing constraints on what can be viewed as a stochastic extension of level sets of Lyapunov functions for deterministic systems. Our approach solves several important problems -- it can be used to learn a control policy from scratch, to verify a reach-avoid specification for a fixed control policy, or to fine-tune a pre-trained policy if it does not satisfy the reach-avoid specification. We validate our approach on $3$ stochastic non-linear reinforcement learning tasks.

Learning Control Policies for Region Stabilization in Stochastic Systems

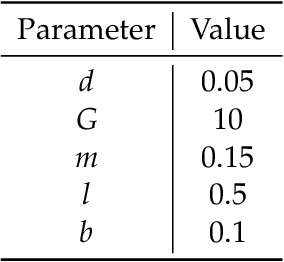
We consider the problem of learning control policies in stochastic systems which guarantee that the system stabilizes within some specified stabilization region with probability $1$. Our approach is based on the novel notion of stabilizing ranking supermartingales (sRSMs) that we introduce in this work. Our sRSMs overcome the limitation of methods proposed in previous works whose applicability is restricted to systems in which the stabilizing region cannot be left once entered under any control policy. We present a learning procedure that learns a control policy together with an sRSM that formally certifies probability-$1$ stability, both learned as neural networks. Our experimental evaluation shows that our learning procedure can successfully learn provably stabilizing policies in practice.

Learning Stabilizing Policies in Stochastic Control Systems

In this work, we address the problem of learning provably stable neural network policies for stochastic control systems. While recent work has demonstrated the feasibility of certifying given policies using martingale theory, the problem of how to learn such policies is little explored. Here, we study the effectiveness of jointly learning a policy together with a martingale certificate that proves its stability using a single learning algorithm. We observe that the joint optimization problem becomes easily stuck in local minima when starting from a randomly initialized policy. Our results suggest that some form of pre-training of the policy is required for the joint optimization to repair and verify the policy successfully.

Stability Verification in Stochastic Control Systems via Neural Network Supermartingales

We consider the problem of formally verifying almost-sure (a.s.) asymptotic stability in discrete-time nonlinear stochastic control systems. While verifying stability in deterministic control systems is extensively studied in the literature, verifying stability in stochastic control systems is an open problem. The few existing works on this topic either consider only specialized forms of stochasticity or make restrictive assumptions on the system, rendering them inapplicable to learning algorithms with neural network policies. In this work, we present an approach for general nonlinear stochastic control problems with two novel aspects: (a) instead of classical stochastic extensions of Lyapunov functions, we use ranking supermartingales (RSMs) to certify a.s.~asymptotic stability, and (b) we present a method for learning neural network RSMs. We prove that our approach guarantees a.s.~asymptotic stability of the system and provides the first method to obtain bounds on the stabilization time, which stochastic Lyapunov functions do not. Finally, we validate our approach experimentally on a set of nonlinear stochastic reinforcement learning environments with neural network policies.