Threshold UCT: Cost-Constrained Monte Carlo Tree Search with Pareto Curves

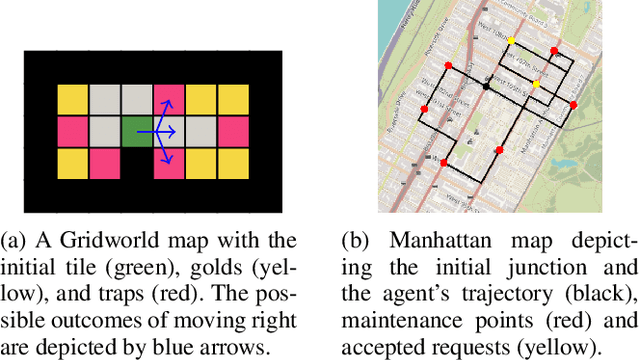
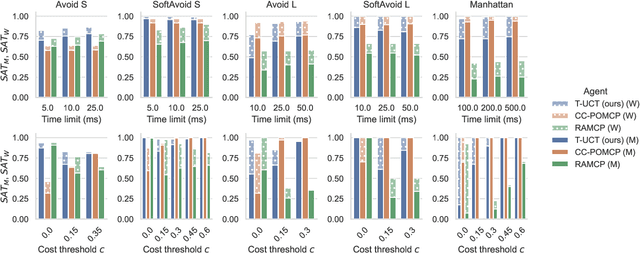
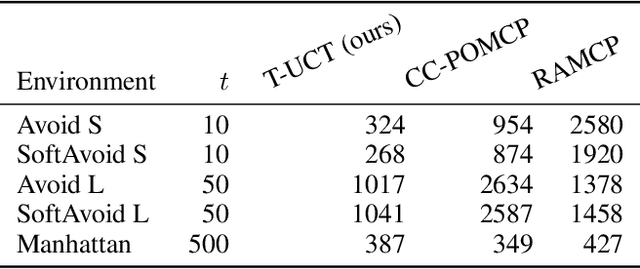
Constrained Markov decision processes (CMDPs), in which the agent optimizes expected payoffs while keeping the expected cost below a given threshold, are the leading framework for safe sequential decision making under stochastic uncertainty. Among algorithms for planning and learning in CMDPs, methods based on Monte Carlo tree search (MCTS) have particular importance due to their efficiency and extendibility to more complex frameworks (such as partially observable settings and games). However, current MCTS-based methods for CMDPs either struggle with finding safe (i.e., constraint-satisfying) policies, or are too conservative and do not find valuable policies. We introduce Threshold UCT (T-UCT), an online MCTS-based algorithm for CMDP planning. Unlike previous MCTS-based CMDP planners, T-UCT explicitly estimates Pareto curves of cost-utility trade-offs throughout the search tree, using these together with a novel action selection and threshold update rules to seek safe and valuable policies. Our experiments demonstrate that our approach significantly outperforms state-of-the-art methods from the literature.

Solving Long-run Average Reward Robust MDPs via Stochastic Games

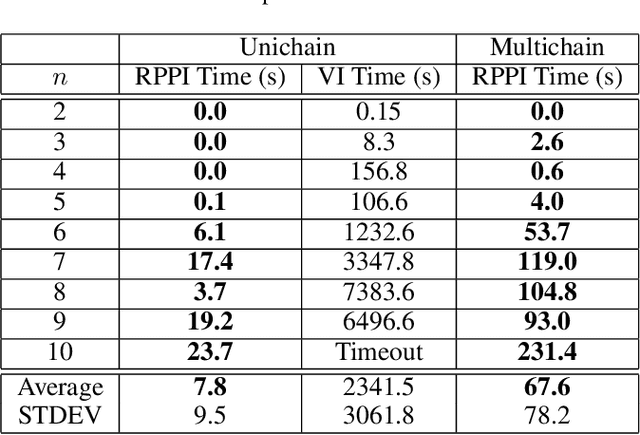
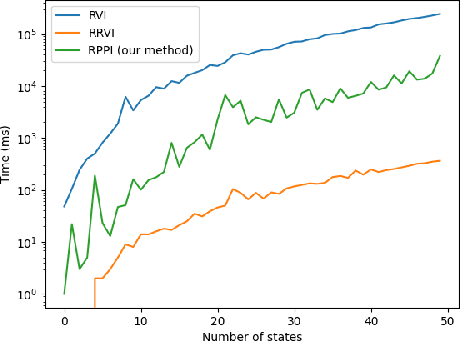
Markov decision processes (MDPs) provide a standard framework for sequential decision making under uncertainty. However, transition probabilities in MDPs are often estimated from data and MDPs do not take data uncertainty into account. Robust Markov decision processes (RMDPs) address this shortcoming of MDPs by assigning to each transition an uncertainty set rather than a single probability value. The goal of solving RMDPs is then to find a policy which maximizes the worst-case performance over the uncertainty sets. In this work, we consider polytopic RMDPs in which all uncertainty sets are polytopes and study the problem of solving long-run average reward polytopic RMDPs. Our focus is on computational complexity aspects and efficient algorithms. We present a novel perspective on this problem and show that it can be reduced to solving long-run average reward turn-based stochastic games with finite state and action spaces. This reduction allows us to derive several important consequences that were hitherto not known to hold for polytopic RMDPs. First, we derive new computational complexity bounds for solving long-run average reward polytopic RMDPs, showing for the first time that the threshold decision problem for them is in NP coNP and that they admit a randomized algorithm with sub-exponential expected runtime. Second, we present Robust Polytopic Policy Iteration (RPPI), a novel policy iteration algorithm for solving long-run average reward polytopic RMDPs. Our experimental evaluation shows that RPPI is much more efficient in solving long-run average reward polytopic RMDPs compared to state-of-the-art methods based on value iteration.

Shielding in Resource-Constrained Goal POMDPs

We consider partially observable Markov decision processes (POMDPs) modeling an agent that needs a supply of a certain resource (e.g., electricity stored in batteries) to operate correctly. The resource is consumed by agent's actions and can be replenished only in certain states. The agent aims to minimize the expected cost of reaching some goal while preventing resource exhaustion, a problem we call \emph{resource-constrained goal optimization} (RSGO). We take a two-step approach to the RSGO problem. First, using formal methods techniques, we design an algorithm computing a \emph{shield} for a given scenario: a procedure that observes the agent and prevents it from using actions that might eventually lead to resource exhaustion. Second, we augment the POMCP heuristic search algorithm for POMDP planning with our shields to obtain an algorithm solving the RSGO problem. We implement our algorithm and present experiments showing its applicability to benchmarks from the literature.

Efficient Strategy Synthesis for MDPs with Resource Constraints

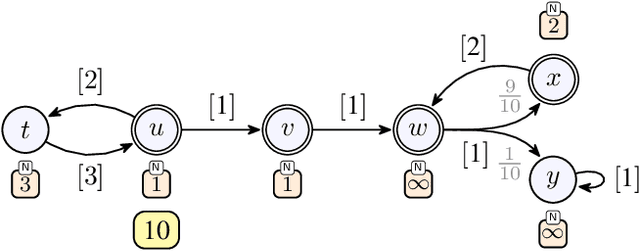
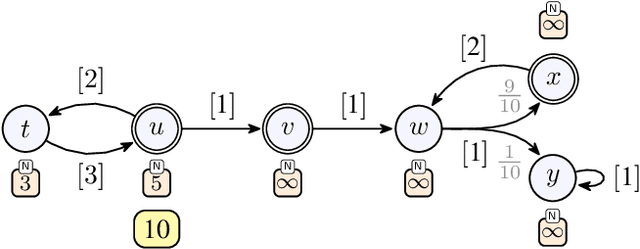
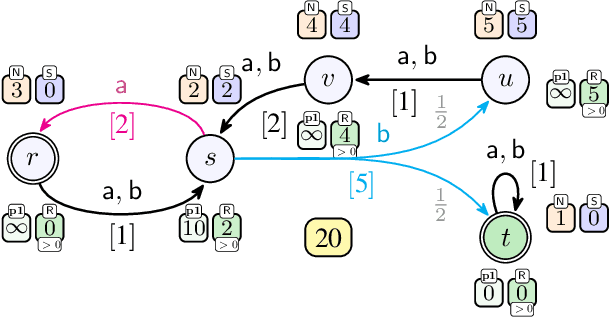
We consider qualitative strategy synthesis for the formalism called consumption Markov decision processes. This formalism can model dynamics of an agents that operates under resource constraints in a stochastic environment. The presented algorithms work in time polynomial with respect to the representation of the model and they synthesize strategies ensuring that a given set of goal states will be reached (once or infinitely many times) with probability 1 without resource exhaustion. In particular, when the amount of resource becomes too low to safely continue in the mission, the strategy changes course of the agent towards one of a designated set of reload states where the agent replenishes the resource to full capacity; with sufficient amount of resource, the agent attempts to fulfill the mission again. We also present two heuristics that attempt to reduce expected time that the agent needs to fulfill the given mission, a parameter important in practical planning. The presented algorithms were implemented and numerical examples demonstrate (i) the effectiveness (in terms of computation time) of the planning approach based on consumption Markov decision processes and (ii) the positive impact of the two heuristics on planning in a realistic example.

On the Complexity of Iterative Tropical Computation with Applications to Markov Decision Processes

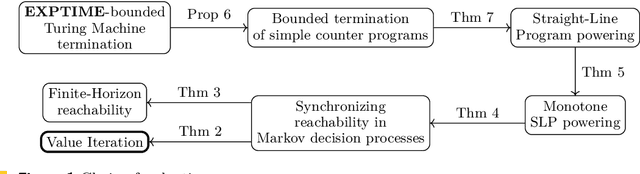
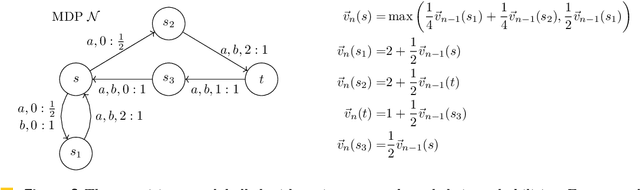
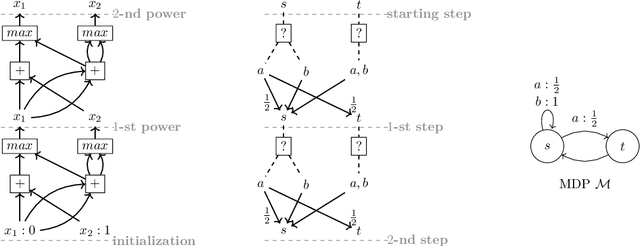
We study the complexity of evaluating powered functions implemented by straight-line programs (SLPs) over the tropical semiring (i.e., with max and + operations). In this problem, a given (max,+)-SLP with the same number of input and output wires is composed with H copies of itself, where H is given in binary. The problem of evaluating powered SLPs is intimately connected with iterative arithmetic computations that arise in algorithmic decision making and operations research. Specifically, it is essentially equivalent to finding optimal strategies in finite-horizon Markov Decision Processes (MDPs). We show that evaluating powered SLPs and finding optimal strategies in finite-horizon MDPs are both EXPTIME-complete problems. This resolves an open problem that goes back to the seminal 1987 paper on the complexity of MDPs by Papadimitriou and Tsitsiklis.

Expectation Optimization with Probabilistic Guarantees in POMDPs with Discounted-sum Objectives

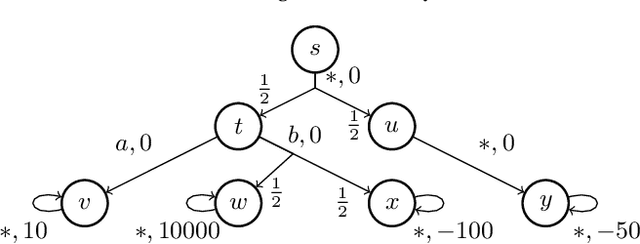
Partially-observable Markov decision processes (POMDPs) with discounted-sum payoff are a standard framework to model a wide range of problems related to decision making under uncertainty. Traditionally, the goal has been to obtain policies that optimize the expectation of the discounted-sum payoff. A key drawback of the expectation measure is that even low probability events with extreme payoff can significantly affect the expectation, and thus the obtained policies are not necessarily risk-averse. An alternate approach is to optimize the probability that the payoff is above a certain threshold, which allows obtaining risk-averse policies, but ignores optimization of the expectation. We consider the expectation optimization with probabilistic guarantee (EOPG) problem, where the goal is to optimize the expectation ensuring that the payoff is above a given threshold with at least a specified probability. We present several results on the EOPG problem, including the first algorithm to solve it.

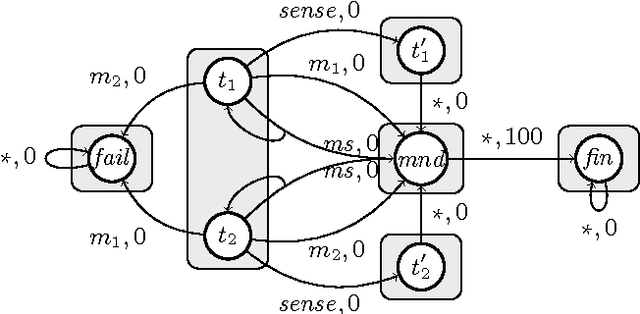
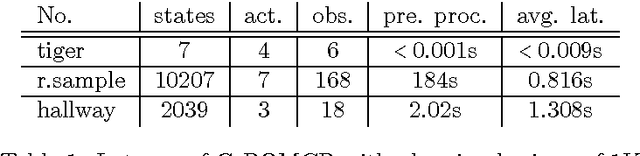
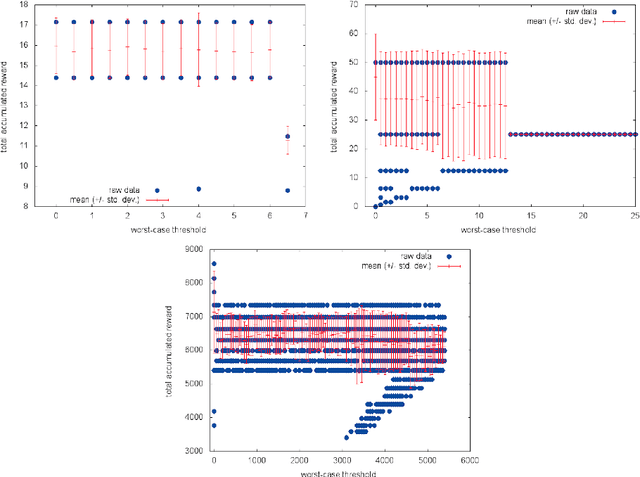
Optimizing Expectation with Guarantees in POMDPs (Technical Report)

A standard objective in partially-observable Markov decision processes (POMDPs) is to find a policy that maximizes the expected discounted-sum payoff. However, such policies may still permit unlikely but highly undesirable outcomes, which is problematic especially in safety-critical applications. Recently, there has been a surge of interest in POMDPs where the goal is to maximize the probability to ensure that the payoff is at least a given threshold, but these approaches do not consider any optimization beyond satisfying this threshold constraint. In this work we go beyond both the "expectation" and "threshold" approaches and consider a "guaranteed payoff optimization (GPO)" problem for POMDPs, where we are given a threshold $t$ and the objective is to find a policy $\sigma$ such that a) each possible outcome of $\sigma$ yields a discounted-sum payoff of at least $t$, and b) the expected discounted-sum payoff of $\sigma$ is optimal (or near-optimal) among all policies satisfying a). We present a practical approach to tackle the GPO problem and evaluate it on standard POMDP benchmarks.

Stochastic Shortest Path with Energy Constraints in POMDPs

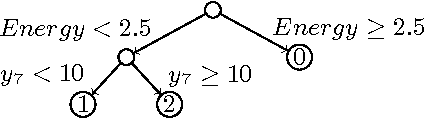
We consider partially observable Markov decision processes (POMDPs) with a set of target states and positive integer costs associated with every transition. The traditional optimization objective (stochastic shortest path) asks to minimize the expected total cost until the target set is reached. We extend the traditional framework of POMDPs to model energy consumption, which represents a hard constraint. The energy levels may increase and decrease with transitions, and the hard constraint requires that the energy level must remain positive in all steps till the target is reached. First, we present a novel algorithm for solving POMDPs with energy levels, developing on existing POMDP solvers and using RTDP as its main method. Our second contribution is related to policy representation. For larger POMDP instances the policies computed by existing solvers are too large to be understandable. We present an automated procedure based on machine learning techniques that automatically extracts important decisions of the policy allowing us to compute succinct human readable policies. Finally, we show experimentally that our algorithm performs well and computes succinct policies on a number of POMDP instances from the literature that were naturally enhanced with energy levels.