Stefan Kiefer
On the Complexity of Iterative Tropical Computation with Applications to Markov Decision Processes
Jul 13, 2018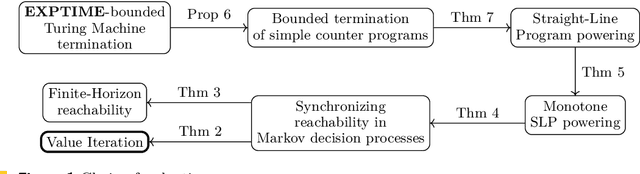
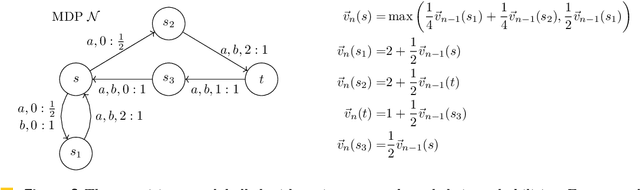
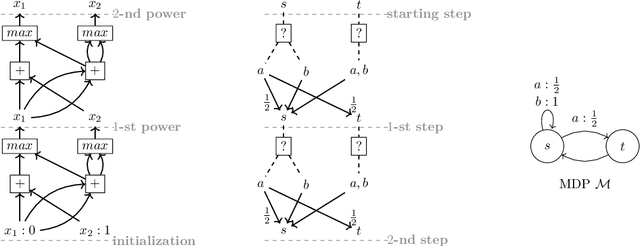
Abstract:We study the complexity of evaluating powered functions implemented by straight-line programs (SLPs) over the tropical semiring (i.e., with max and + operations). In this problem, a given (max,+)-SLP with the same number of input and output wires is composed with H copies of itself, where H is given in binary. The problem of evaluating powered SLPs is intimately connected with iterative arithmetic computations that arise in algorithmic decision making and operations research. Specifically, it is essentially equivalent to finding optimal strategies in finite-horizon Markov Decision Processes (MDPs). We show that evaluating powered SLPs and finding optimal strategies in finite-horizon MDPs are both EXPTIME-complete problems. This resolves an open problem that goes back to the seminal 1987 paper on the complexity of MDPs by Papadimitriou and Tsitsiklis.
Nonnegative Matrix Factorization Requires Irrationality
Mar 22, 2017



Abstract:Nonnegative matrix factorization (NMF) is the problem of decomposing a given nonnegative $n \times m$ matrix $M$ into a product of a nonnegative $n \times d$ matrix $W$ and a nonnegative $d \times m$ matrix $H$. A longstanding open question, posed by Cohen and Rothblum in 1993, is whether a rational matrix $M$ always has an NMF of minimal inner dimension $d$ whose factors $W$ and $H$ are also rational. We answer this question negatively, by exhibiting a matrix for which $W$ and $H$ require irrational entries.
On Restricted Nonnegative Matrix Factorization
May 23, 2016



Abstract:Nonnegative matrix factorization (NMF) is the problem of decomposing a given nonnegative $n \times m$ matrix $M$ into a product of a nonnegative $n \times d$ matrix $W$ and a nonnegative $d \times m$ matrix $H$. Restricted NMF requires in addition that the column spaces of $M$ and $W$ coincide. Finding the minimal inner dimension $d$ is known to be NP-hard, both for NMF and restricted NMF. We show that restricted NMF is closely related to a question about the nature of minimal probabilistic automata, posed by Paz in his seminal 1971 textbook. We use this connection to answer Paz's question negatively, thus falsifying a positive answer claimed in 1974. Furthermore, we investigate whether a rational matrix $M$ always has a restricted NMF of minimal inner dimension whose factors $W$ and $H$ are also rational. We show that this holds for matrices $M$ of rank at most $3$ and we exhibit a rank-$4$ matrix for which $W$ and $H$ require irrational entries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge