Revelations: A Decidable Class of POMDPs with Omega-Regular Objectives

Partially observable Markov decision processes (POMDPs) form a prominent model for uncertainty in sequential decision making. We are interested in constructing algorithms with theoretical guarantees to determine whether the agent has a strategy ensuring a given specification with probability 1. This well-studied problem is known to be undecidable already for very simple omega-regular objectives, because of the difficulty of reasoning on uncertain events. We introduce a revelation mechanism which restricts information loss by requiring that almost surely the agent has eventually full information of the current state. Our main technical results are to construct exact algorithms for two classes of POMDPs called weakly and strongly revealing. Importantly, the decidable cases reduce to the analysis of a finite belief-support Markov decision process. This yields a conceptually simple and exact algorithm for a large class of POMDPs.

Active Learning of Mealy Machines with Timers

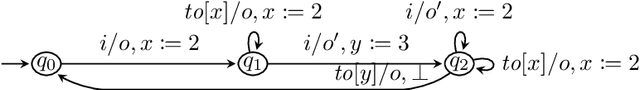
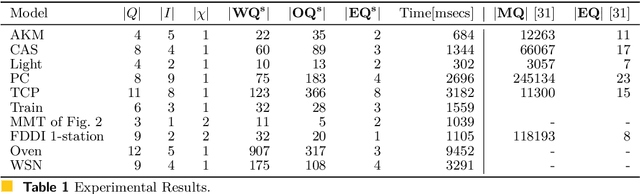
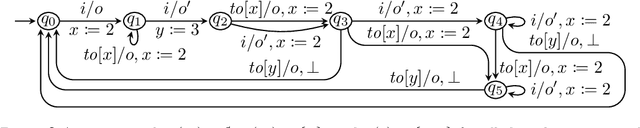
We present the first algorithm for query learning of a general class of Mealy machines with timers (MMTs) in a black-box context. Our algorithm is an extension of the L# algorithm of Vaandrager et al. to a timed setting. Like the algorithm for learning timed automata proposed by Waga, our algorithm is inspired by ideas of Maler & Pnueli. Based on the elementary languages of, both Waga's and our algorithm use symbolic queries, which are then implemented using finitely many concrete queries. However, whereas Waga needs exponentially many concrete queries to implement a single symbolic query, we only need a polynomial number. This is because in order to learn a timed automaton, a learner needs to determine the exact guard and reset for each transition (out of exponentially many possibilities), whereas for learning an MMT a learner only needs to figure out which of the preceding transitions caused a timeout. As shown in our previous work, this can be done efficiently for a subclass of MMTs that are race-avoiding: if a timeout is caused by a preceding input then a slight change in the timing of this input will induce a corresponding change in the timing of the timeout ("wiggling"). Experiments with a prototype implementation, written in Rust, show that our algorithm is able to efficiently learn realistic benchmarks.

Synthesis of Hierarchical Controllers Based on Deep Reinforcement Learning Policies

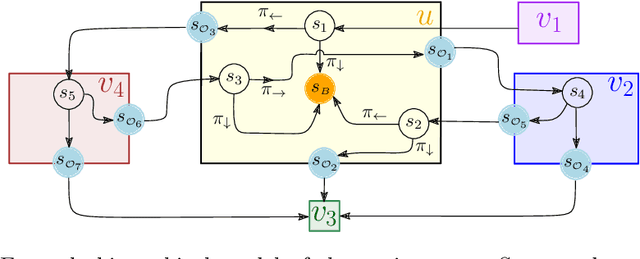
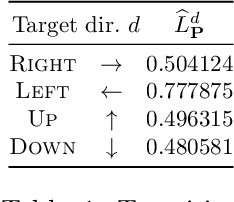
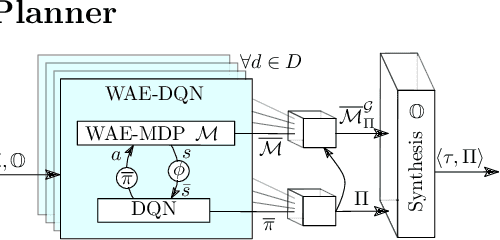
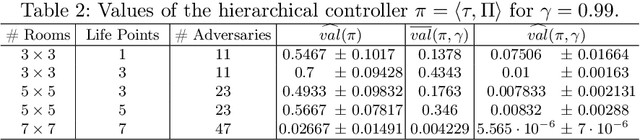
We propose a novel approach to the problem of controller design for environments modeled as Markov decision processes (MDPs). Specifically, we consider a hierarchical MDP a graph with each vertex populated by an MDP called a "room". We first apply deep reinforcement learning (DRL) to obtain low-level policies for each room, scaling to large rooms of unknown structure. We then apply reactive synthesis to obtain a high-level planner that chooses which low-level policy to execute in each room. The central challenge in synthesizing the planner is the need for modeling rooms. We address this challenge by developing a DRL procedure to train concise "latent" policies together with PAC guarantees on their performance. Unlike previous approaches, ours circumvents a model distillation step. Our approach combats sparse rewards in DRL and enables reusability of low-level policies. We demonstrate feasibility in a case study involving agent navigation amid moving obstacles.

Formally-Sharp DAgger for MCTS: Lower-Latency Monte Carlo Tree Search using Data Aggregation with Formal Methods

We study how to efficiently combine formal methods, Monte Carlo Tree Search (MCTS), and deep learning in order to produce high-quality receding horizon policies in large Markov Decision processes (MDPs). In particular, we use model-checking techniques to guide the MCTS algorithm in order to generate offline samples of high-quality decisions on a representative set of states of the MDP. Those samples can then be used to train a neural network that imitates the policy used to generate them. This neural network can either be used as a guide on a lower-latency MCTS online search, or alternatively be used as a full-fledged policy when minimal latency is required. We use statistical model checking to detect when additional samples are needed and to focus those additional samples on configurations where the learnt neural network policy differs from the (computationally-expensive) offline policy. We illustrate the use of our method on MDPs that model the Frozen Lake and Pac-Man environments -- two popular benchmarks to evaluate reinforcement-learning algorithms.

Graph-Based Reductions for Parametric and Weighted MDPs

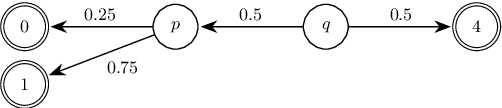
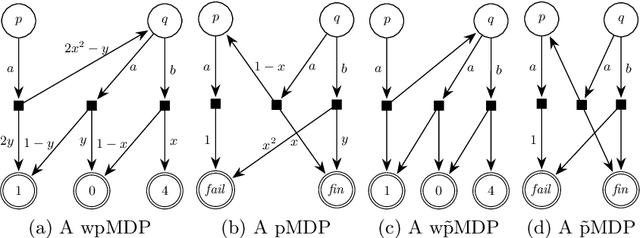
We study the complexity of reductions for weighted reachability in parametric Markov decision processes. That is, we say a state p is never worse than q if for all valuations of the polynomial indeterminates it is the case that the maximal expected weight that can be reached from p is greater than the same value from q. In terms of computational complexity, we establish that determining whether p is never worse than q is coETR-complete. On the positive side, we give a polynomial-time algorithm to compute the equivalence classes of the order we study for Markov chains. Additionally, we describe and implement two inference rules to under-approximate the never-worse relation and empirically show that it can be used as an efficient preprocessing step for the analysis of large Markov decision processes.

Wasserstein Auto-encoded MDPs: Formal Verification of Efficiently Distilled RL Policies with Many-sided Guarantees

Although deep reinforcement learning (DRL) has many success stories, the large-scale deployment of policies learned through these advanced techniques in safety-critical scenarios is hindered by their lack of formal guarantees. Variational Markov Decision Processes (VAE-MDPs) are discrete latent space models that provide a reliable framework for distilling formally verifiable controllers from any RL policy. While the related guarantees address relevant practical aspects such as the satisfaction of performance and safety properties, the VAE approach suffers from several learning flaws (posterior collapse, slow learning speed, poor dynamics estimates), primarily due to the absence of abstraction and representation guarantees to support latent optimization. We introduce the Wasserstein auto-encoded MDP (WAE-MDP), a latent space model that fixes those issues by minimizing a penalized form of the optimal transport between the behaviors of the agent executing the original policy and the distilled policy, for which the formal guarantees apply. Our approach yields bisimulation guarantees while learning the distilled policy, allowing concrete optimization of the abstraction and representation model quality. Our experiments show that, besides distilling policies up to 10 times faster, the latent model quality is indeed better in general. Moreover, we present experiments from a simple time-to-failure verification algorithm on the latent space. The fact that our approach enables such simple verification techniques highlights its applicability.

The Wasserstein Believer: Learning Belief Updates for Partially Observable Environments through Reliable Latent Space Models

Partially Observable Markov Decision Processes (POMDPs) are useful tools to model environments where the full state cannot be perceived by an agent. As such the agent needs to reason taking into account the past observations and actions. However, simply remembering the full history is generally intractable due to the exponential growth in the history space. Keeping a probability distribution that models the belief over what the true state is can be used as a sufficient statistic of the history, but its computation requires access to the model of the environment and is also intractable. Current state-of-the-art algorithms use Recurrent Neural Networks (RNNs) to compress the observation-action history aiming to learn a sufficient statistic, but they lack guarantees of success and can lead to suboptimal policies. To overcome this, we propose the Wasserstein-Belief-Updater (WBU), an RL algorithm that learns a latent model of the POMDP and an approximation of the belief update. Our approach comes with theoretical guarantees on the quality of our approximation ensuring that our outputted beliefs allow for learning the optimal value function.

Distillation of RL Policies with Formal Guarantees via Variational Abstraction of Markov Decision Processes (Technical Report)

We consider the challenge of policy simplification and verification in the context of policies learned through reinforcement learning (RL) in continuous environments. In well-behaved settings, RL algorithms have convergence guarantees in the limit. While these guarantees are valuable, they are insufficient for safety-critical applications. Furthermore, they are lost when applying advanced techniques such as deep-RL. To recover guarantees when applying advanced RL algorithms to more complex environments with (i) reachability, (ii) safety-constrained reachability, or (iii) discounted-reward objectives, we build upon the DeepMDP framework introduced by Gelada et al. to derive new bisimulation bounds between the unknown environment and a learned discrete latent model of it. Our bisimulation bounds enable the application of formal methods for Markov decision processes. Finally, we show how one can use a policy obtained via state-of-the-art RL to efficiently train a variational autoencoder that yields a discrete latent model with provably approximately correct bisimulation guarantees. Additionally, we obtain a distilled version of the policy for the latent model.

Safe Learning for Near Optimal Scheduling

In this paper, we investigate the combination of synthesis techniques and learning techniques to obtain safe and near optimal schedulers for a preemptible task scheduling problem. We study both model-based learning techniques with PAC guarantees and model-free learning techniques based on shielded deep Q-learning. The new learning algorithms have been implemented to conduct experimental evaluations.

Robustness Verification for Classifier Ensembles

We give a formal verification procedure that decides whether a classifier ensemble is robust against arbitrary randomized attacks. Such attacks consist of a set of deterministic attacks and a distribution over this set. The robustness-checking problem consists of assessing, given a set of classifiers and a labelled data set, whether there exists a randomized attack that induces a certain expected loss against all classifiers. We show the NP-hardness of the problem and provide an upper bound on the number of attacks that is sufficient to form an optimal randomized attack. These results provide an effective way to reason about the robustness of a classifier ensemble. We provide SMT and MILP encodings to compute optimal randomized attacks or prove that there is no attack inducing a certain expected loss. In the latter case, the classifier ensemble is provably robust. Our prototype implementation verifies multiple neural-network ensembles trained for image-classification tasks. The experimental results using the MILP encoding are promising both in terms of scalability and the general applicability of our verification procedure.