Bharat Garhewal
Active Learning of Mealy Machines with Timers
Mar 04, 2024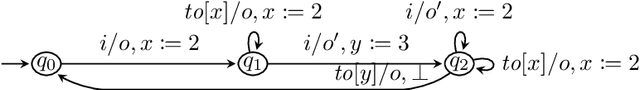
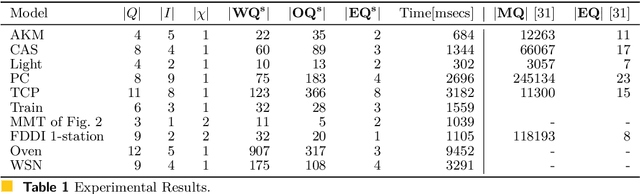
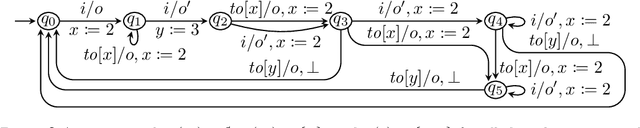

Abstract:We present the first algorithm for query learning of a general class of Mealy machines with timers (MMTs) in a black-box context. Our algorithm is an extension of the L# algorithm of Vaandrager et al. to a timed setting. Like the algorithm for learning timed automata proposed by Waga, our algorithm is inspired by ideas of Maler & Pnueli. Based on the elementary languages of, both Waga's and our algorithm use symbolic queries, which are then implemented using finitely many concrete queries. However, whereas Waga needs exponentially many concrete queries to implement a single symbolic query, we only need a polynomial number. This is because in order to learn a timed automaton, a learner needs to determine the exact guard and reset for each transition (out of exponentially many possibilities), whereas for learning an MMT a learner only needs to figure out which of the preceding transitions caused a timeout. As shown in our previous work, this can be done efficiently for a subclass of MMTs that are race-avoiding: if a timeout is caused by a preceding input then a slight change in the timing of this input will induce a corresponding change in the timing of the timeout ("wiggling"). Experiments with a prototype implementation, written in Rust, show that our algorithm is able to efficiently learn realistic benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge