ShiQ: Bringing back Bellman to LLMs

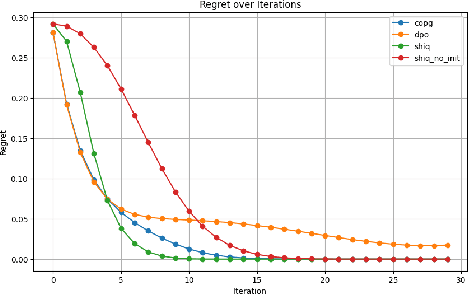
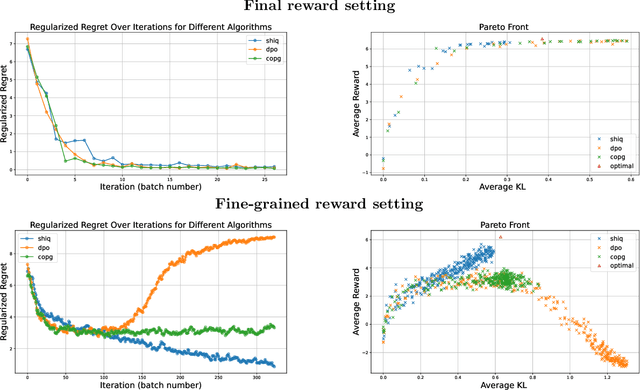
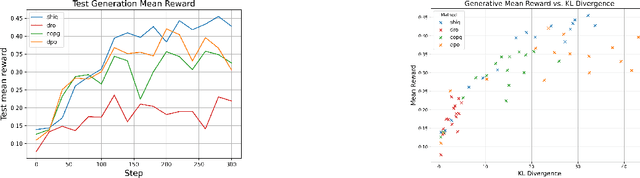
The fine-tuning of pre-trained large language models (LLMs) using reinforcement learning (RL) is generally formulated as direct policy optimization. This approach was naturally favored as it efficiently improves a pretrained LLM, seen as an initial policy. Another RL paradigm, Q-learning methods, has received far less attention in the LLM community while demonstrating major success in various non-LLM RL tasks. In particular, Q-learning effectiveness comes from its sample efficiency and ability to learn offline, which is particularly valuable given the high computational cost of sampling with LLMs. However, naively applying a Q-learning-style update to the model's logits is ineffective due to the specificity of LLMs. Our core contribution is to derive theoretically grounded loss functions from Bellman equations to adapt Q-learning methods to LLMs. To do so, we carefully adapt insights from the RL literature to account for LLM-specific characteristics, ensuring that the logits become reliable Q-value estimates. We then use this loss to build a practical algorithm, ShiQ for Shifted-Q, that supports off-policy, token-wise learning while remaining simple to implement. Finally, we evaluate ShiQ on both synthetic data and real-world benchmarks, e.g., UltraFeedback and BFCL-V3, demonstrating its effectiveness in both single-turn and multi-turn LLM settings

Online Planning in POMDPs with State-Requests

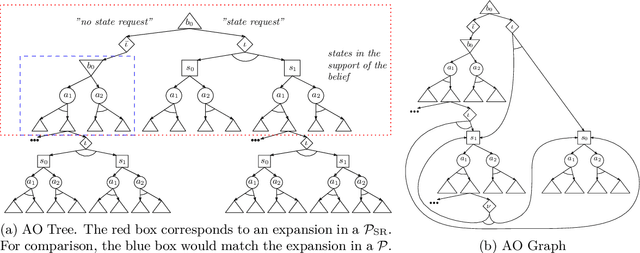
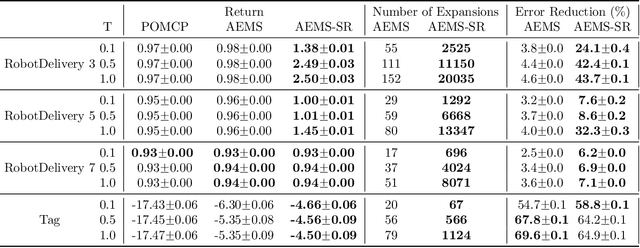
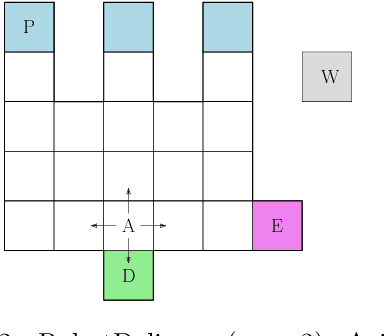
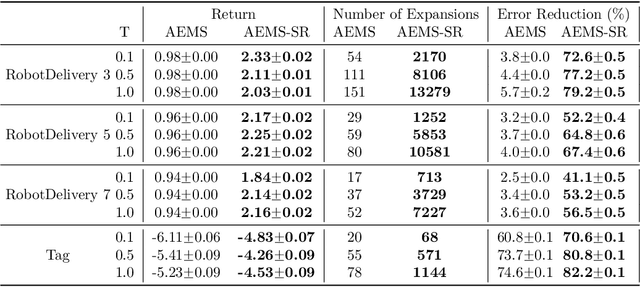
In key real-world problems, full state information is sometimes available but only at a high cost, like activating precise yet energy-intensive sensors or consulting humans, thereby compelling the agent to operate under partial observability. For this scenario, we propose AEMS-SR (Anytime Error Minimization Search with State Requests), a principled online planning algorithm tailored for POMDPs with state requests. By representing the search space as a graph instead of a tree, AEMS-SR avoids the exponential growth of the search space originating from state requests. Theoretical analysis demonstrates AEMS-SR's $\varepsilon$-optimality, ensuring solution quality, while empirical evaluations illustrate its effectiveness compared with AEMS and POMCP, two SOTA online planning algorithms. AEMS-SR enables efficient planning in domains characterized by partial observability and costly state requests offering practical benefits across various applications.

The Wasserstein Believer: Learning Belief Updates for Partially Observable Environments through Reliable Latent Space Models

Partially Observable Markov Decision Processes (POMDPs) are useful tools to model environments where the full state cannot be perceived by an agent. As such the agent needs to reason taking into account the past observations and actions. However, simply remembering the full history is generally intractable due to the exponential growth in the history space. Keeping a probability distribution that models the belief over what the true state is can be used as a sufficient statistic of the history, but its computation requires access to the model of the environment and is also intractable. Current state-of-the-art algorithms use Recurrent Neural Networks (RNNs) to compress the observation-action history aiming to learn a sufficient statistic, but they lack guarantees of success and can lead to suboptimal policies. To overcome this, we propose the Wasserstein-Belief-Updater (WBU), an RL algorithm that learns a latent model of the POMDP and an approximation of the belief update. Our approach comes with theoretical guarantees on the quality of our approximation ensuring that our outputted beliefs allow for learning the optimal value function.