Synthesis of Hierarchical Controllers Based on Deep Reinforcement Learning Policies

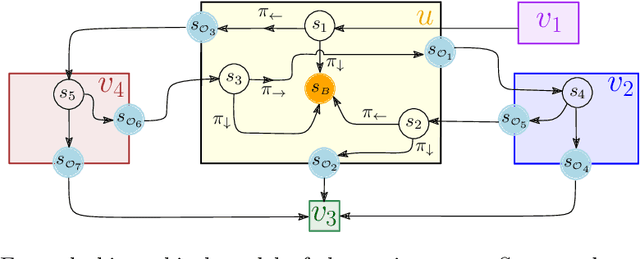
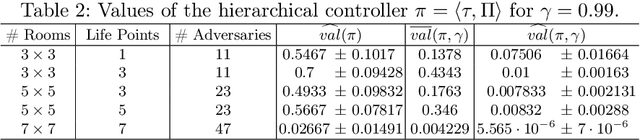
We propose a novel approach to the problem of controller design for environments modeled as Markov decision processes (MDPs). Specifically, we consider a hierarchical MDP a graph with each vertex populated by an MDP called a "room". We first apply deep reinforcement learning (DRL) to obtain low-level policies for each room, scaling to large rooms of unknown structure. We then apply reactive synthesis to obtain a high-level planner that chooses which low-level policy to execute in each room. The central challenge in synthesizing the planner is the need for modeling rooms. We address this challenge by developing a DRL procedure to train concise "latent" policies together with PAC guarantees on their performance. Unlike previous approaches, ours circumvents a model distillation step. Our approach combats sparse rewards in DRL and enables reusability of low-level policies. We demonstrate feasibility in a case study involving agent navigation amid moving obstacles.

Wasserstein Auto-encoded MDPs: Formal Verification of Efficiently Distilled RL Policies with Many-sided Guarantees

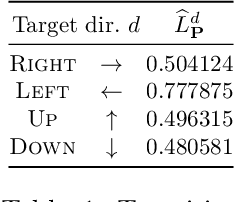
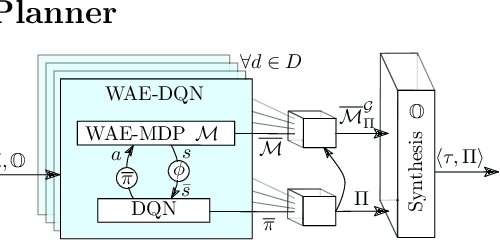
Although deep reinforcement learning (DRL) has many success stories, the large-scale deployment of policies learned through these advanced techniques in safety-critical scenarios is hindered by their lack of formal guarantees. Variational Markov Decision Processes (VAE-MDPs) are discrete latent space models that provide a reliable framework for distilling formally verifiable controllers from any RL policy. While the related guarantees address relevant practical aspects such as the satisfaction of performance and safety properties, the VAE approach suffers from several learning flaws (posterior collapse, slow learning speed, poor dynamics estimates), primarily due to the absence of abstraction and representation guarantees to support latent optimization. We introduce the Wasserstein auto-encoded MDP (WAE-MDP), a latent space model that fixes those issues by minimizing a penalized form of the optimal transport between the behaviors of the agent executing the original policy and the distilled policy, for which the formal guarantees apply. Our approach yields bisimulation guarantees while learning the distilled policy, allowing concrete optimization of the abstraction and representation model quality. Our experiments show that, besides distilling policies up to 10 times faster, the latent model quality is indeed better in general. Moreover, we present experiments from a simple time-to-failure verification algorithm on the latent space. The fact that our approach enables such simple verification techniques highlights its applicability.

The Wasserstein Believer: Learning Belief Updates for Partially Observable Environments through Reliable Latent Space Models

Partially Observable Markov Decision Processes (POMDPs) are useful tools to model environments where the full state cannot be perceived by an agent. As such the agent needs to reason taking into account the past observations and actions. However, simply remembering the full history is generally intractable due to the exponential growth in the history space. Keeping a probability distribution that models the belief over what the true state is can be used as a sufficient statistic of the history, but its computation requires access to the model of the environment and is also intractable. Current state-of-the-art algorithms use Recurrent Neural Networks (RNNs) to compress the observation-action history aiming to learn a sufficient statistic, but they lack guarantees of success and can lead to suboptimal policies. To overcome this, we propose the Wasserstein-Belief-Updater (WBU), an RL algorithm that learns a latent model of the POMDP and an approximation of the belief update. Our approach comes with theoretical guarantees on the quality of our approximation ensuring that our outputted beliefs allow for learning the optimal value function.

Distillation of RL Policies with Formal Guarantees via Variational Abstraction of Markov Decision Processes (Technical Report)

We consider the challenge of policy simplification and verification in the context of policies learned through reinforcement learning (RL) in continuous environments. In well-behaved settings, RL algorithms have convergence guarantees in the limit. While these guarantees are valuable, they are insufficient for safety-critical applications. Furthermore, they are lost when applying advanced techniques such as deep-RL. To recover guarantees when applying advanced RL algorithms to more complex environments with (i) reachability, (ii) safety-constrained reachability, or (iii) discounted-reward objectives, we build upon the DeepMDP framework introduced by Gelada et al. to derive new bisimulation bounds between the unknown environment and a learned discrete latent model of it. Our bisimulation bounds enable the application of formal methods for Markov decision processes. Finally, we show how one can use a policy obtained via state-of-the-art RL to efficiently train a variational autoencoder that yields a discrete latent model with provably approximately correct bisimulation guarantees. Additionally, we obtain a distilled version of the policy for the latent model.

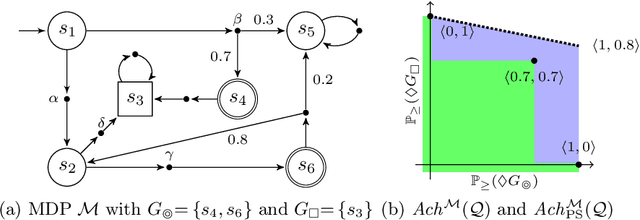
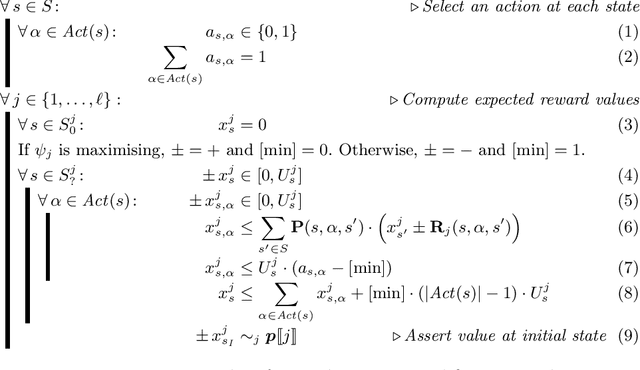
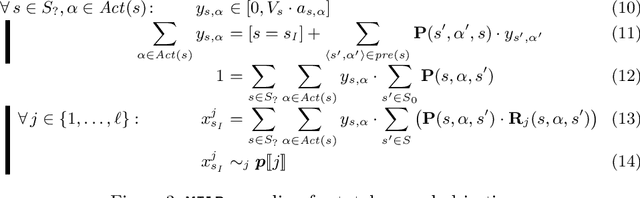
Simple Strategies in Multi-Objective MDPs (Technical Report)

We consider the verification of multiple expected reward objectives at once on Markov decision processes (MDPs). This enables a trade-off analysis among multiple objectives by obtaining the Pareto front. We focus on strategies that are easy to employ and implement. That is, strategies that are pure (no randomization) and have bounded memory. We show that checking whether a point is achievable by a pure stationary strategy is NP-complete, even for two objectives, and we provide an MILP encoding to solve the corresponding problem. The bounded memory case can be reduced to the stationary one by a product construction. Experimental results using \Storm and Gurobi show the feasibility of our algorithms.

Life is Random, Time is Not: Markov Decision Processes with Window Objectives

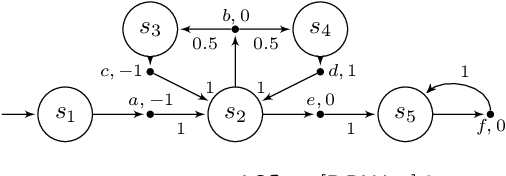
The window mechanism was introduced by Chatterjee et al. [1] to strengthen classical game objectives with time bounds. It permits to synthesize system controllers that exhibit acceptable behaviors within a configurable time frame, all along their infinite execution, in contrast to the traditional objectives that only require correctness of behaviors in the limit. The window concept has proved its interest in a variety of two-player zero-sum games, thanks to the ability to reason about such time bounds in system specifications, but also the increased tractability that it usually yields. In this work, we extend the window framework to stochastic environments by considering the fundamental threshold probability problem in Markov decision processes for window objectives. That is, given such an objective, we want to synthesize strategies that guarantee satisfying runs with a given probability. We solve this problem for the usual variants of window objectives, where either the time frame is set as a parameter, or we ask if such a time frame exists. We develop a generic approach for window-based objectives and instantiate it for the classical mean-payoff and parity objectives, already considered in games. Our work paves the way to a wide use of the window mechanism in stochastic models. [1] Krishnendu Chatterjee, Laurent Doyen, Mickael Randour, and Jean-Fran\c{c}ois Raskin. Looking at mean-payoff and total-payoff through windows. Inf. Comput., 242:25-52, 2015.