Scalable Multi-Objective Reinforcement Learning with Fairness Guarantees using Lorenz Dominance

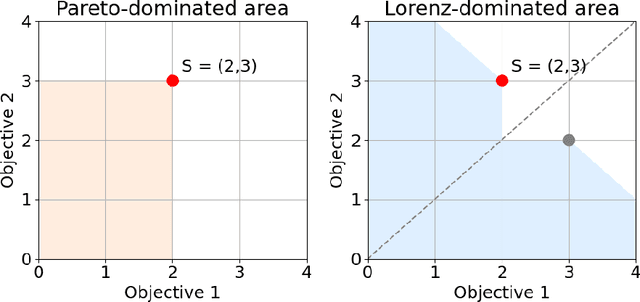
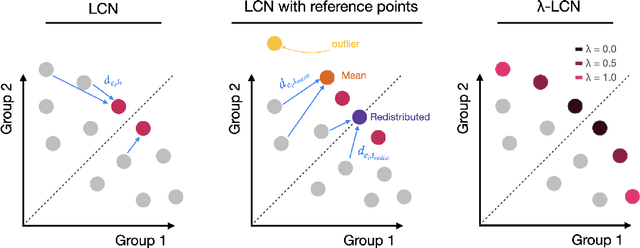
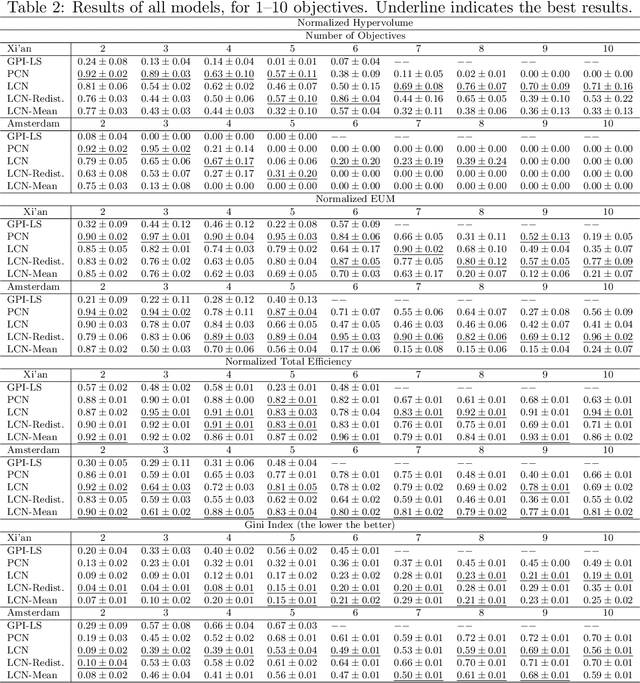
Multi-Objective Reinforcement Learning (MORL) aims to learn a set of policies that optimize trade-offs between multiple, often conflicting objectives. MORL is computationally more complex than single-objective RL, particularly as the number of objectives increases. Additionally, when objectives involve the preferences of agents or groups, ensuring fairness is socially desirable. This paper introduces a principled algorithm that incorporates fairness into MORL while improving scalability to many-objective problems. We propose using Lorenz dominance to identify policies with equitable reward distributions and introduce {\lambda}-Lorenz dominance to enable flexible fairness preferences. We release a new, large-scale real-world transport planning environment and demonstrate that our method encourages the discovery of fair policies, showing improved scalability in two large cities (Xi'an and Amsterdam). Our methods outperform common multi-objective approaches, particularly in high-dimensional objective spaces.

Online Planning in POMDPs with State-Requests

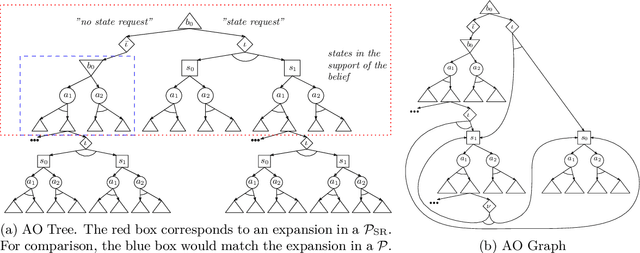
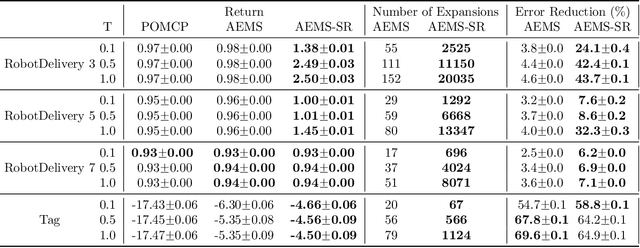
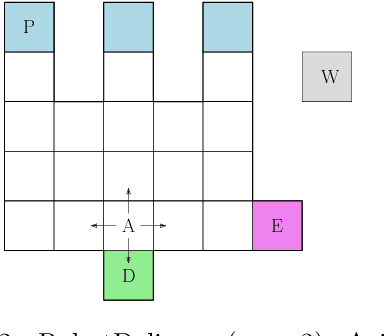
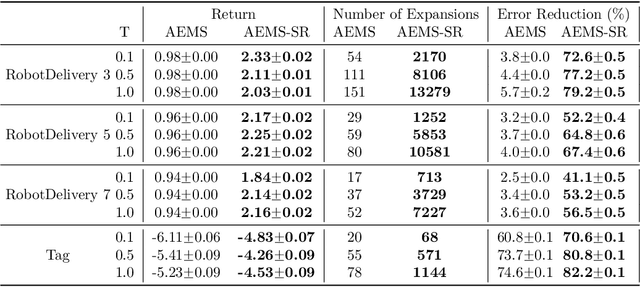
In key real-world problems, full state information is sometimes available but only at a high cost, like activating precise yet energy-intensive sensors or consulting humans, thereby compelling the agent to operate under partial observability. For this scenario, we propose AEMS-SR (Anytime Error Minimization Search with State Requests), a principled online planning algorithm tailored for POMDPs with state requests. By representing the search space as a graph instead of a tree, AEMS-SR avoids the exponential growth of the search space originating from state requests. Theoretical analysis demonstrates AEMS-SR's $\varepsilon$-optimality, ensuring solution quality, while empirical evaluations illustrate its effectiveness compared with AEMS and POMCP, two SOTA online planning algorithms. AEMS-SR enables efficient planning in domains characterized by partial observability and costly state requests offering practical benefits across various applications.

MOMAland: A Set of Benchmarks for Multi-Objective Multi-Agent Reinforcement Learning

Many challenging tasks such as managing traffic systems, electricity grids, or supply chains involve complex decision-making processes that must balance multiple conflicting objectives and coordinate the actions of various independent decision-makers (DMs). One perspective for formalising and addressing such tasks is multi-objective multi-agent reinforcement learning (MOMARL). MOMARL broadens reinforcement learning (RL) to problems with multiple agents each needing to consider multiple objectives in their learning process. In reinforcement learning research, benchmarks are crucial in facilitating progress, evaluation, and reproducibility. The significance of benchmarks is underscored by the existence of numerous benchmark frameworks developed for various RL paradigms, including single-agent RL (e.g., Gymnasium), multi-agent RL (e.g., PettingZoo), and single-agent multi-objective RL (e.g., MO-Gymnasium). To support the advancement of the MOMARL field, we introduce MOMAland, the first collection of standardised environments for multi-objective multi-agent reinforcement learning. MOMAland addresses the need for comprehensive benchmarking in this emerging field, offering over 10 diverse environments that vary in the number of agents, state representations, reward structures, and utility considerations. To provide strong baselines for future research, MOMAland also includes algorithms capable of learning policies in such settings.

Deep Multi-Objective Reinforcement Learning for Utility-Based Infrastructural Maintenance Optimization

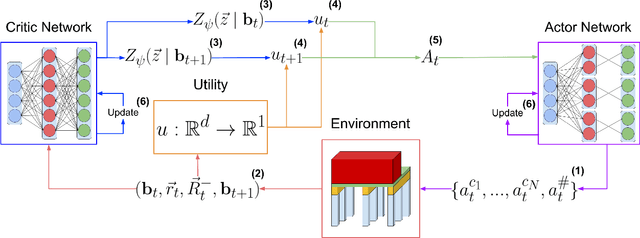
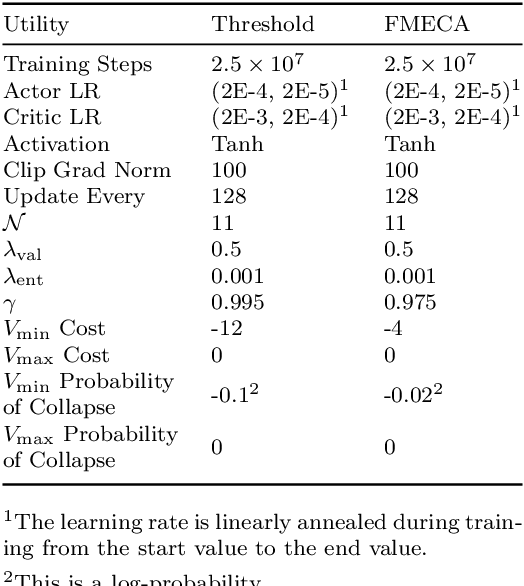
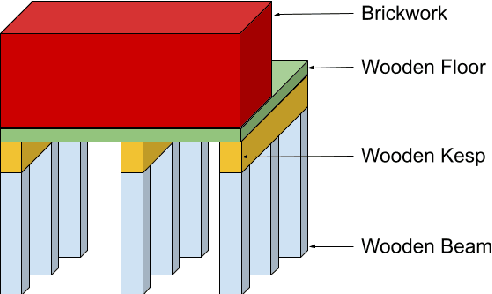
In this paper, we introduce Multi-Objective Deep Centralized Multi-Agent Actor-Critic (MO- DCMAC), a multi-objective reinforcement learning (MORL) method for infrastructural maintenance optimization, an area traditionally dominated by single-objective reinforcement learning (RL) approaches. Previous single-objective RL methods combine multiple objectives, such as probability of collapse and cost, into a singular reward signal through reward-shaping. In contrast, MO-DCMAC can optimize a policy for multiple objectives directly, even when the utility function is non-linear. We evaluated MO-DCMAC using two utility functions, which use probability of collapse and cost as input. The first utility function is the Threshold utility, in which MO-DCMAC should minimize cost so that the probability of collapse is never above the threshold. The second is based on the Failure Mode, Effects, and Criticality Analysis (FMECA) methodology used by asset managers to asses maintenance plans. We evaluated MO-DCMAC, with both utility functions, in multiple maintenance environments, including ones based on a case study of the historical quay walls of Amsterdam. The performance of MO-DCMAC was compared against multiple rule-based policies based on heuristics currently used for constructing maintenance plans. Our results demonstrate that MO-DCMAC outperforms traditional rule-based policies across various environments and utility functions.

Divide and Conquer: Provably Unveiling the Pareto Front with Multi-Objective Reinforcement Learning

A significant challenge in multi-objective reinforcement learning is obtaining a Pareto front of policies that attain optimal performance under different preferences. We introduce Iterated Pareto Referent Optimisation (IPRO), a principled algorithm that decomposes the task of finding the Pareto front into a sequence of single-objective problems for which various solution methods exist. This enables us to establish convergence guarantees while providing an upper bound on the distance to undiscovered Pareto optimal solutions at each step. Empirical evaluations demonstrate that IPRO matches or outperforms methods that require additional domain knowledge. By leveraging problem-specific single-objective solvers, our approach also holds promise for applications beyond multi-objective reinforcement learning, such as in pathfinding and optimisation.

Utility-Based Reinforcement Learning: Unifying Single-objective and Multi-objective Reinforcement Learning

Research in multi-objective reinforcement learning (MORL) has introduced the utility-based paradigm, which makes use of both environmental rewards and a function that defines the utility derived by the user from those rewards. In this paper we extend this paradigm to the context of single-objective reinforcement learning (RL), and outline multiple potential benefits including the ability to perform multi-policy learning across tasks relating to uncertain objectives, risk-aware RL, discounting, and safe RL. We also examine the algorithmic implications of adopting a utility-based approach.

What Lies beyond the Pareto Front? A Survey on Decision-Support Methods for Multi-Objective Optimization

We present a review that unifies decision-support methods for exploring the solutions produced by multi-objective optimization (MOO) algorithms. As MOO is applied to solve diverse problems, approaches for analyzing the trade-offs offered by MOO algorithms are scattered across fields. We provide an overview of the advances on this topic, including methods for visualization, mining the solution set, and uncertainty exploration as well as emerging research directions, including interactivity, explainability, and ethics. We synthesize these methods drawing from different fields of research to build a unified approach, independent of the application. Our goals are to reduce the entry barrier for researchers and practitioners on using MOO algorithms and to provide novel research directions.

Distributional Multi-Objective Decision Making

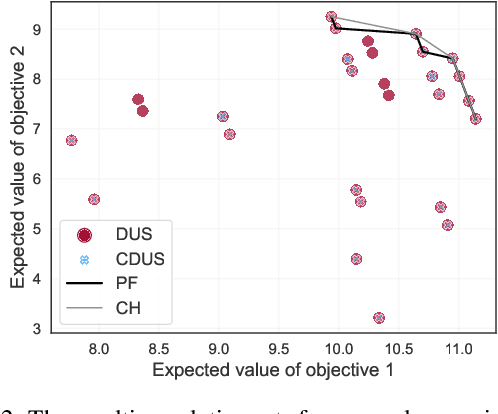
For effective decision support in scenarios with conflicting objectives, sets of potentially optimal solutions can be presented to the decision maker. We explore both what policies these sets should contain and how such sets can be computed efficiently. With this in mind, we take a distributional approach and introduce a novel dominance criterion relating return distributions of policies directly. Based on this criterion, we present the distributional undominated set and show that it contains optimal policies otherwise ignored by the Pareto front. In addition, we propose the convex distributional undominated set and prove that it comprises all policies that maximise expected utility for multivariate risk-averse decision makers. We propose a novel algorithm to learn the distributional undominated set and further contribute pruning operators to reduce the set to the convex distributional undominated set. Through experiments, we demonstrate the feasibility and effectiveness of these methods, making this a valuable new approach for decision support in real-world problems.

The Wasserstein Believer: Learning Belief Updates for Partially Observable Environments through Reliable Latent Space Models

Partially Observable Markov Decision Processes (POMDPs) are useful tools to model environments where the full state cannot be perceived by an agent. As such the agent needs to reason taking into account the past observations and actions. However, simply remembering the full history is generally intractable due to the exponential growth in the history space. Keeping a probability distribution that models the belief over what the true state is can be used as a sufficient statistic of the history, but its computation requires access to the model of the environment and is also intractable. Current state-of-the-art algorithms use Recurrent Neural Networks (RNNs) to compress the observation-action history aiming to learn a sufficient statistic, but they lack guarantees of success and can lead to suboptimal policies. To overcome this, we propose the Wasserstein-Belief-Updater (WBU), an RL algorithm that learns a latent model of the POMDP and an approximation of the belief update. Our approach comes with theoretical guarantees on the quality of our approximation ensuring that our outputted beliefs allow for learning the optimal value function.

Sample-Efficient Multi-Objective Learning via Generalized Policy Improvement Prioritization

Multi-objective reinforcement learning (MORL) algorithms tackle sequential decision problems where agents may have different preferences over (possibly conflicting) reward functions. Such algorithms often learn a set of policies (each optimized for a particular agent preference) that can later be used to solve problems with novel preferences. We introduce a novel algorithm that uses Generalized Policy Improvement (GPI) to define principled, formally-derived prioritization schemes that improve sample-efficient learning. They implement active-learning strategies by which the agent can (i) identify the most promising preferences/objectives to train on at each moment, to more rapidly solve a given MORL problem; and (ii) identify which previous experiences are most relevant when learning a policy for a particular agent preference, via a novel Dyna-style MORL method. We prove our algorithm is guaranteed to always converge to an optimal solution in a finite number of steps, or an $\epsilon$-optimal solution (for a bounded $\epsilon$) if the agent is limited and can only identify possibly sub-optimal policies. We also prove that our method monotonically improves the quality of its partial solutions while learning. Finally, we introduce a bound that characterizes the maximum utility loss (with respect to the optimal solution) incurred by the partial solutions computed by our method throughout learning. We empirically show that our method outperforms state-of-the-art MORL algorithms in challenging multi-objective tasks, both with discrete and continuous state spaces.