Sample-Efficient Multi-Objective Learning via Generalized Policy Improvement Prioritization

Multi-objective reinforcement learning (MORL) algorithms tackle sequential decision problems where agents may have different preferences over (possibly conflicting) reward functions. Such algorithms often learn a set of policies (each optimized for a particular agent preference) that can later be used to solve problems with novel preferences. We introduce a novel algorithm that uses Generalized Policy Improvement (GPI) to define principled, formally-derived prioritization schemes that improve sample-efficient learning. They implement active-learning strategies by which the agent can (i) identify the most promising preferences/objectives to train on at each moment, to more rapidly solve a given MORL problem; and (ii) identify which previous experiences are most relevant when learning a policy for a particular agent preference, via a novel Dyna-style MORL method. We prove our algorithm is guaranteed to always converge to an optimal solution in a finite number of steps, or an $\epsilon$-optimal solution (for a bounded $\epsilon$) if the agent is limited and can only identify possibly sub-optimal policies. We also prove that our method monotonically improves the quality of its partial solutions while learning. Finally, we introduce a bound that characterizes the maximum utility loss (with respect to the optimal solution) incurred by the partial solutions computed by our method throughout learning. We empirically show that our method outperforms state-of-the-art MORL algorithms in challenging multi-objective tasks, both with discrete and continuous state spaces.

Optimistic Linear Support and Successor Features as a Basis for Optimal Policy Transfer

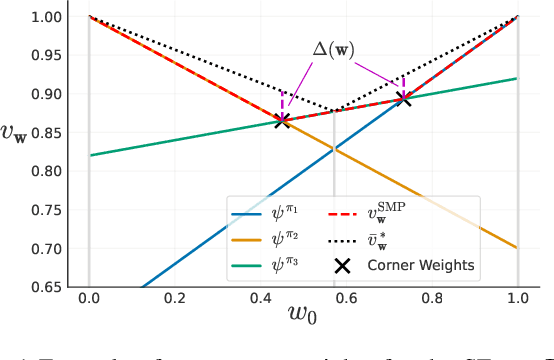
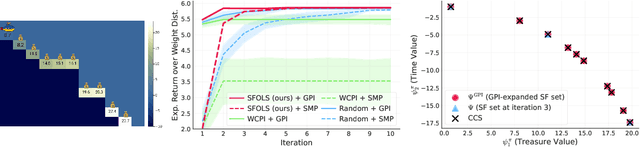
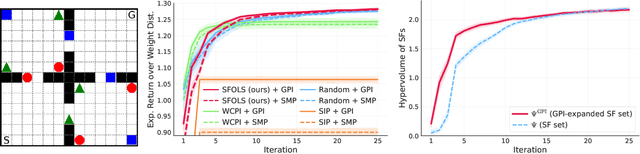
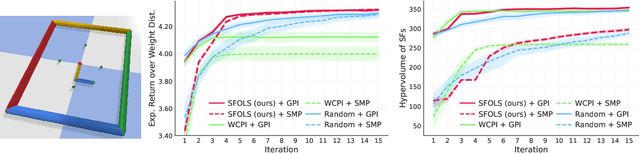
In many real-world applications, reinforcement learning (RL) agents might have to solve multiple tasks, each one typically modeled via a reward function. If reward functions are expressed linearly, and the agent has previously learned a set of policies for different tasks, successor features (SFs) can be exploited to combine such policies and identify reasonable solutions for new problems. However, the identified solutions are not guaranteed to be optimal. We introduce a novel algorithm that addresses this limitation. It allows RL agents to combine existing policies and directly identify optimal policies for arbitrary new problems, without requiring any further interactions with the environment. We first show (under mild assumptions) that the transfer learning problem tackled by SFs is equivalent to the problem of learning to optimize multiple objectives in RL. We then introduce an SF-based extension of the Optimistic Linear Support algorithm to learn a set of policies whose SFs form a convex coverage set. We prove that policies in this set can be combined via generalized policy improvement to construct optimal behaviors for any new linearly-expressible tasks, without requiring any additional training samples. We empirically show that our method outperforms state-of-the-art competing algorithms both in discrete and continuous domains under value function approximation.

Minimum-Delay Adaptation in Non-Stationary Reinforcement Learning via Online High-Confidence Change-Point Detection

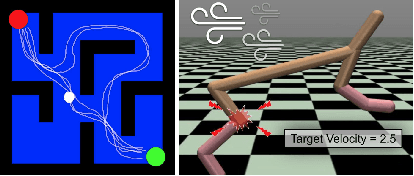
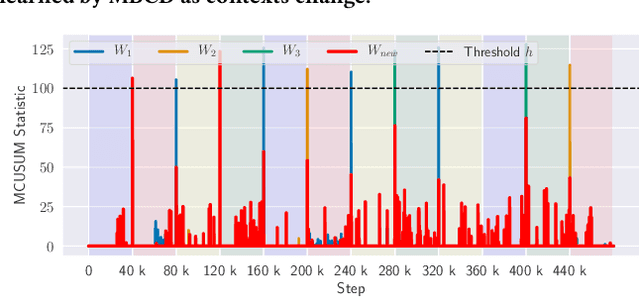
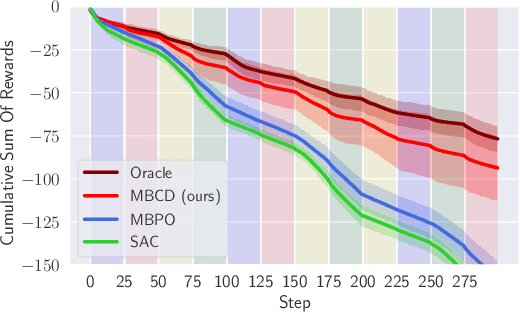
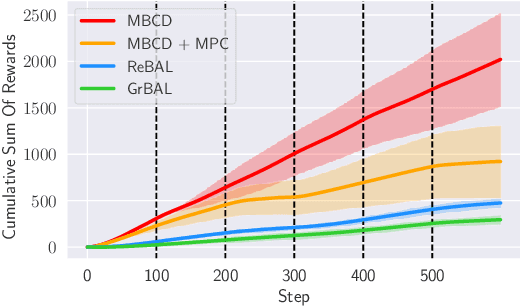
Non-stationary environments are challenging for reinforcement learning algorithms. If the state transition and/or reward functions change based on latent factors, the agent is effectively tasked with optimizing a behavior that maximizes performance over a possibly infinite random sequence of Markov Decision Processes (MDPs), each of which drawn from some unknown distribution. We call each such MDP a context. Most related works make strong assumptions such as knowledge about the distribution over contexts, the existence of pre-training phases, or a priori knowledge about the number, sequence, or boundaries between contexts. We introduce an algorithm that efficiently learns policies in non-stationary environments. It analyzes a possibly infinite stream of data and computes, in real-time, high-confidence change-point detection statistics that reflect whether novel, specialized policies need to be created and deployed to tackle novel contexts, or whether previously-optimized ones might be reused. We show that (i) this algorithm minimizes the delay until unforeseen changes to a context are detected, thereby allowing for rapid responses; and (ii) it bounds the rate of false alarm, which is important in order to minimize regret. Our method constructs a mixture model composed of a (possibly infinite) ensemble of probabilistic dynamics predictors that model the different modes of the distribution over underlying latent MDPs. We evaluate our algorithm on high-dimensional continuous reinforcement learning problems and show that it outperforms state-of-the-art (model-free and model-based) RL algorithms, as well as state-of-the-art meta-learning methods specially designed to deal with non-stationarity.

Quantifying the Impact of Non-Stationarity in Reinforcement Learning-Based Traffic Signal Control

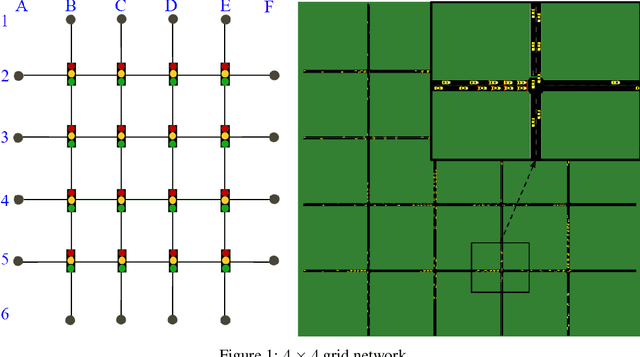
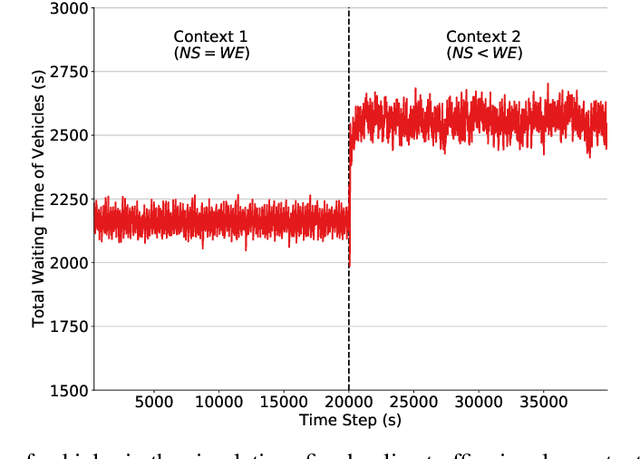
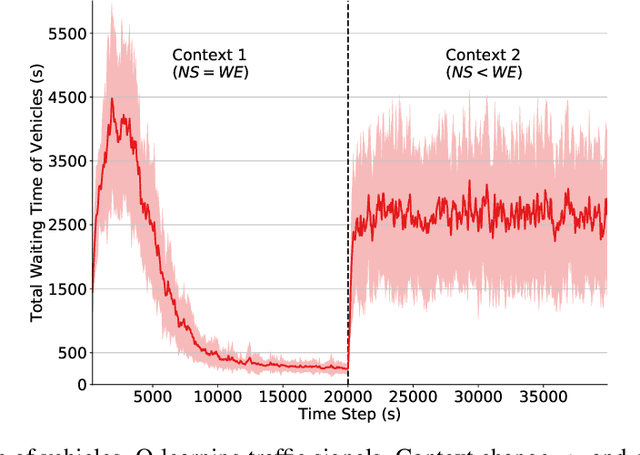
In reinforcement learning (RL), dealing with non-stationarity is a challenging issue. However, some domains such as traffic optimization are inherently non-stationary. Causes for and effects of this are manifold. In particular, when dealing with traffic signal controls, addressing non-stationarity is key since traffic conditions change over time and as a function of traffic control decisions taken in other parts of a network. In this paper we analyze the effects that different sources of non-stationarity have in a network of traffic signals, in which each signal is modeled as a learning agent. More precisely, we study both the effects of changing the \textit{context} in which an agent learns (e.g., a change in flow rates experienced by it), as well as the effects of reducing agent observability of the true environment state. Partial observability may cause distinct states (in which distinct actions are optimal) to be seen as the same by the traffic signal agents. This, in turn, may lead to sub-optimal performance. We show that the lack of suitable sensors to provide a representative observation of the real state seems to affect the performance more drastically than the changes to the underlying traffic patterns.

A Compression-Inspired Framework for Macro Discovery

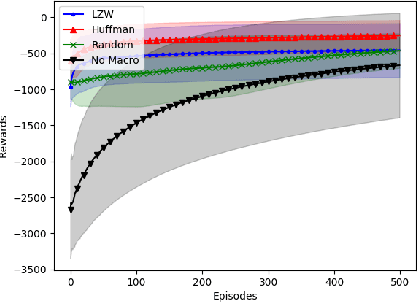
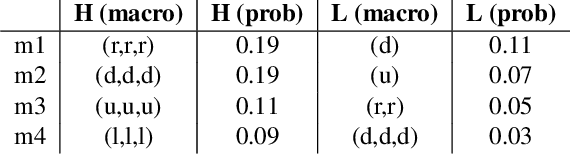
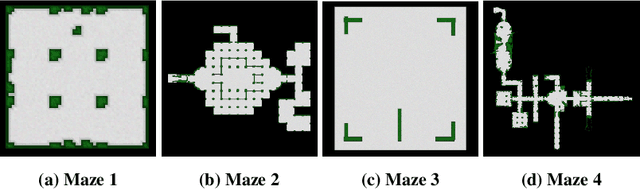
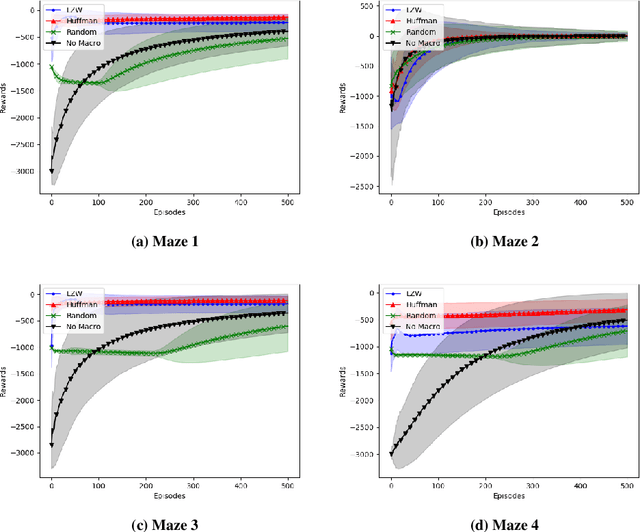
In this paper we consider the problem of how a reinforcement learning agent tasked with solving a set of related Markov decision processes can use knowledge acquired early in its lifetime to improve its ability to more rapidly solve novel, but related, tasks. One way of exploiting this experience is by identifying recurrent patterns in trajectories obtained from well-performing policies. We propose a three-step framework in which an agent 1) generates a set of candidate open-loop macros by compressing trajectories drawn from near-optimal policies; 2) evaluates the value of each macro; and 3) selects a maximally diverse subset of macros that spans the space of policies typically required for solving the set of related tasks. Our experiments show that extending the original primitive action-set of the agent with the identified macros allows it to more rapidly learn an optimal policy in unseen, but similar MDPs.