Optimistic Linear Support and Successor Features as a Basis for Optimal Policy Transfer
Paper and Code
Jun 22, 2022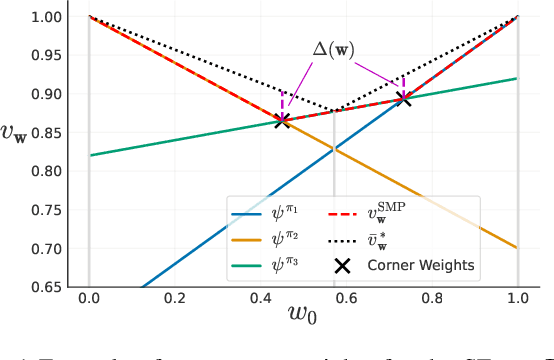
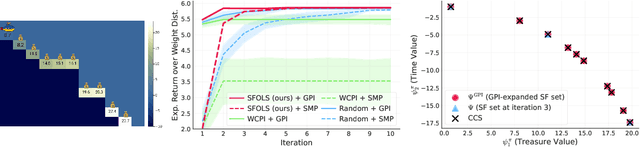
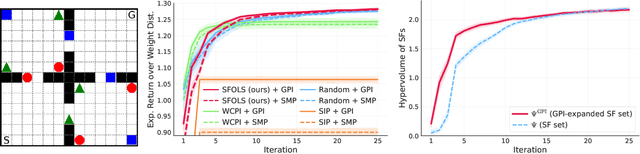
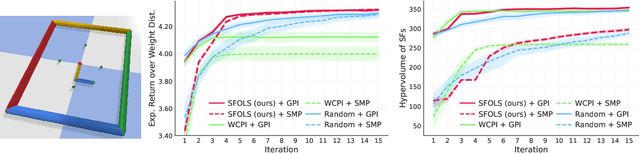
In many real-world applications, reinforcement learning (RL) agents might have to solve multiple tasks, each one typically modeled via a reward function. If reward functions are expressed linearly, and the agent has previously learned a set of policies for different tasks, successor features (SFs) can be exploited to combine such policies and identify reasonable solutions for new problems. However, the identified solutions are not guaranteed to be optimal. We introduce a novel algorithm that addresses this limitation. It allows RL agents to combine existing policies and directly identify optimal policies for arbitrary new problems, without requiring any further interactions with the environment. We first show (under mild assumptions) that the transfer learning problem tackled by SFs is equivalent to the problem of learning to optimize multiple objectives in RL. We then introduce an SF-based extension of the Optimistic Linear Support algorithm to learn a set of policies whose SFs form a convex coverage set. We prove that policies in this set can be combined via generalized policy improvement to construct optimal behaviors for any new linearly-expressible tasks, without requiring any additional training samples. We empirically show that our method outperforms state-of-the-art competing algorithms both in discrete and continuous domains under value function approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge