Minimum-Delay Adaptation in Non-Stationary Reinforcement Learning via Online High-Confidence Change-Point Detection
Paper and Code
May 20, 2021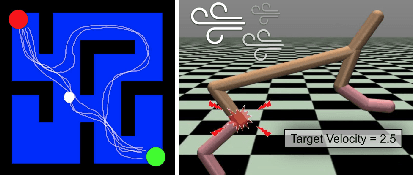
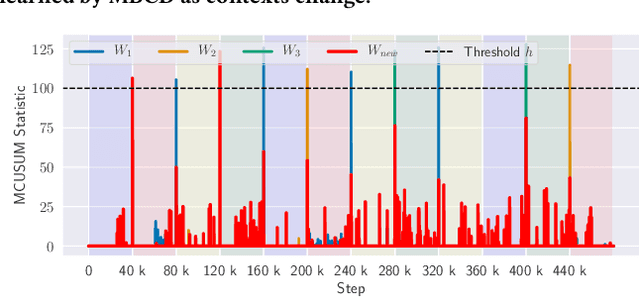
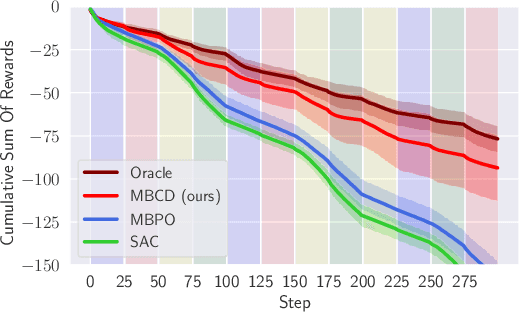
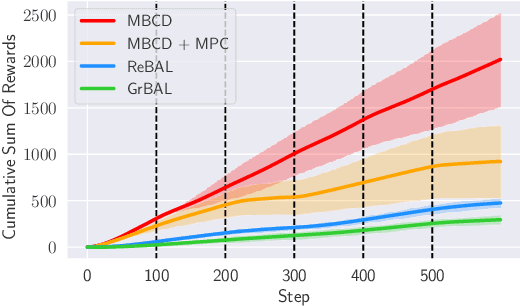
Non-stationary environments are challenging for reinforcement learning algorithms. If the state transition and/or reward functions change based on latent factors, the agent is effectively tasked with optimizing a behavior that maximizes performance over a possibly infinite random sequence of Markov Decision Processes (MDPs), each of which drawn from some unknown distribution. We call each such MDP a context. Most related works make strong assumptions such as knowledge about the distribution over contexts, the existence of pre-training phases, or a priori knowledge about the number, sequence, or boundaries between contexts. We introduce an algorithm that efficiently learns policies in non-stationary environments. It analyzes a possibly infinite stream of data and computes, in real-time, high-confidence change-point detection statistics that reflect whether novel, specialized policies need to be created and deployed to tackle novel contexts, or whether previously-optimized ones might be reused. We show that (i) this algorithm minimizes the delay until unforeseen changes to a context are detected, thereby allowing for rapid responses; and (ii) it bounds the rate of false alarm, which is important in order to minimize regret. Our method constructs a mixture model composed of a (possibly infinite) ensemble of probabilistic dynamics predictors that model the different modes of the distribution over underlying latent MDPs. We evaluate our algorithm on high-dimensional continuous reinforcement learning problems and show that it outperforms state-of-the-art (model-free and model-based) RL algorithms, as well as state-of-the-art meta-learning methods specially designed to deal with non-stationarity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge