Under-Approximating Expected Total Rewards in POMDPs

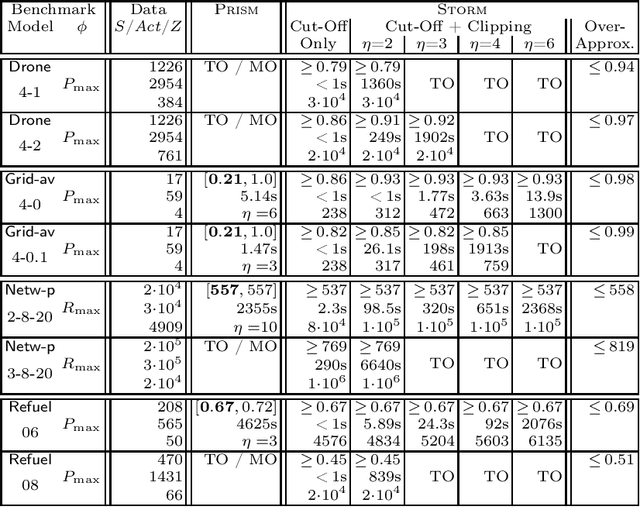
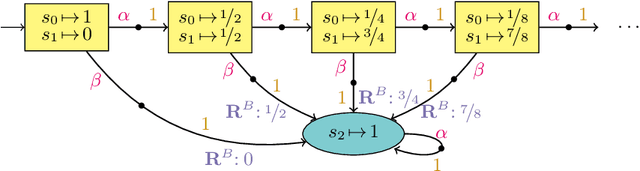
We consider the problem: is the optimal expected total reward to reach a goal state in a partially observable Markov decision process (POMDP) below a given threshold? We tackle this -- generally undecidable -- problem by computing under-approximations on these total expected rewards. This is done by abstracting finite unfoldings of the infinite belief MDP of the POMDP. The key issue is to find a suitable under-approximation of the value function. We provide two techniques: a simple (cut-off) technique that uses a good policy on the POMDP, and a more advanced technique (belief clipping) that uses minimal shifts of probabilities between beliefs. We use mixed-integer linear programming (MILP) to find such minimal probability shifts and experimentally show that our techniques scale quite well while providing tight lower bounds on the expected total reward.

Verification of indefinite-horizon POMDPs

The verification problem in MDPs asks whether, for any policy resolving the nondeterminism, the probability that something bad happens is bounded by some given threshold. This verification problem is often overly pessimistic, as the policies it considers may depend on the complete system state. This paper considers the verification problem for partially observable MDPs, in which the policies make their decisions based on (the history of) the observations emitted by the system. We present an abstraction-refinement framework extending previous instantiations of the Lovejoy-approach. Our experiments show that this framework significantly improves the scalability of the approach.

Simple Strategies in Multi-Objective MDPs (Technical Report)

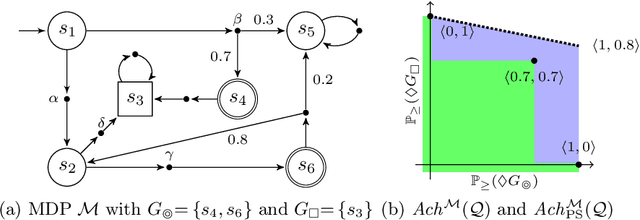
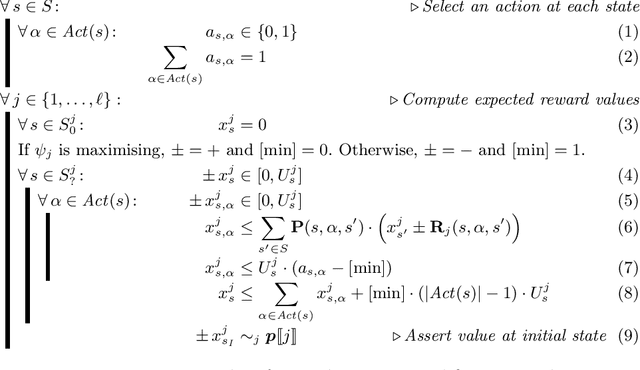
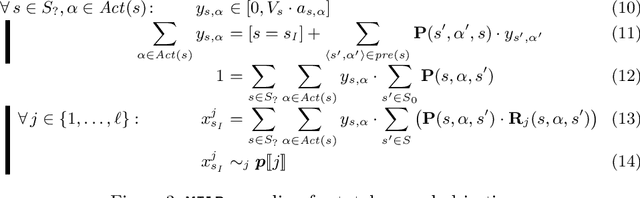
We consider the verification of multiple expected reward objectives at once on Markov decision processes (MDPs). This enables a trade-off analysis among multiple objectives by obtaining the Pareto front. We focus on strategies that are easy to employ and implement. That is, strategies that are pure (no randomization) and have bounded memory. We show that checking whether a point is achievable by a pure stationary strategy is NP-complete, even for two objectives, and we provide an MILP encoding to solve the corresponding problem. The bounded memory case can be reduced to the stationary one by a product construction. Experimental results using \Storm and Gurobi show the feasibility of our algorithms.