Alexander Bork
Learning Explainable and Better Performing Representations of POMDP Strategies
Jan 20, 2024



Abstract:Strategies for partially observable Markov decision processes (POMDP) typically require memory. One way to represent this memory is via automata. We present a method to learn an automaton representation of a strategy using a modification of the L*-algorithm. Compared to the tabular representation of a strategy, the resulting automaton is dramatically smaller and thus also more explainable. Moreover, in the learning process, our heuristics may even improve the strategy's performance. In contrast to approaches that synthesize an automaton directly from the POMDP thereby solving it, our approach is incomparably more scalable.
Under-Approximating Expected Total Rewards in POMDPs
Jan 21, 2022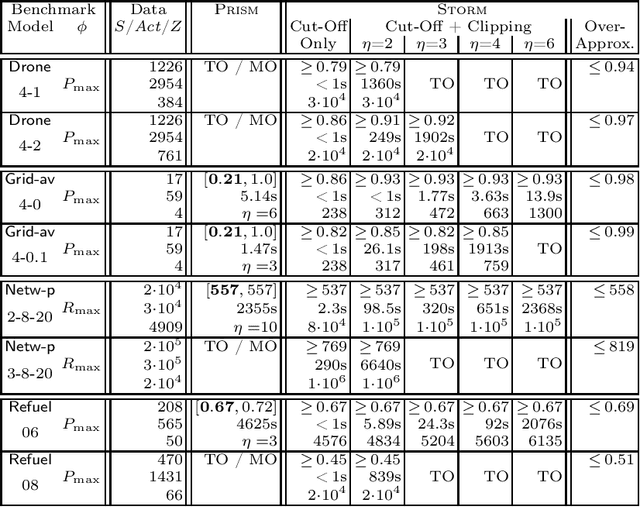


Abstract:We consider the problem: is the optimal expected total reward to reach a goal state in a partially observable Markov decision process (POMDP) below a given threshold? We tackle this -- generally undecidable -- problem by computing under-approximations on these total expected rewards. This is done by abstracting finite unfoldings of the infinite belief MDP of the POMDP. The key issue is to find a suitable under-approximation of the value function. We provide two techniques: a simple (cut-off) technique that uses a good policy on the POMDP, and a more advanced technique (belief clipping) that uses minimal shifts of probabilities between beliefs. We use mixed-integer linear programming (MILP) to find such minimal probability shifts and experimentally show that our techniques scale quite well while providing tight lower bounds on the expected total reward.
Verification of indefinite-horizon POMDPs
Jun 30, 2020



Abstract:The verification problem in MDPs asks whether, for any policy resolving the nondeterminism, the probability that something bad happens is bounded by some given threshold. This verification problem is often overly pessimistic, as the policies it considers may depend on the complete system state. This paper considers the verification problem for partially observable MDPs, in which the policies make their decisions based on (the history of) the observations emitted by the system. We present an abstraction-refinement framework extending previous instantiations of the Lovejoy-approach. Our experiments show that this framework significantly improves the scalability of the approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge