Simple Strategies in Multi-Objective MDPs (Technical Report)
Paper and Code
Oct 25, 2019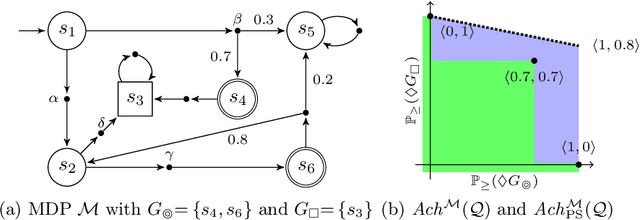
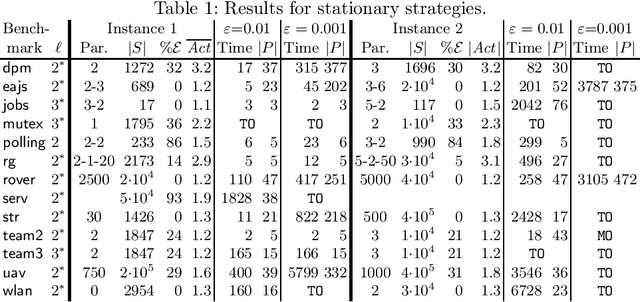
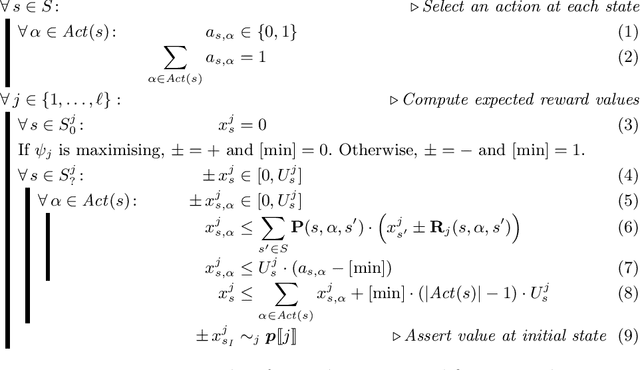
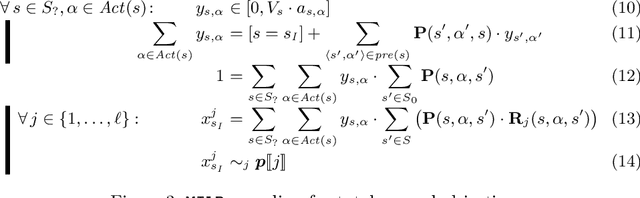
We consider the verification of multiple expected reward objectives at once on Markov decision processes (MDPs). This enables a trade-off analysis among multiple objectives by obtaining the Pareto front. We focus on strategies that are easy to employ and implement. That is, strategies that are pure (no randomization) and have bounded memory. We show that checking whether a point is achievable by a pure stationary strategy is NP-complete, even for two objectives, and we provide an MILP encoding to solve the corresponding problem. The bounded memory case can be reduced to the stationary one by a product construction. Experimental results using \Storm and Gurobi show the feasibility of our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge