Bidding Games on Markov Decision Processes with Quantitative Reachability Objectives

Graph games are fundamental in strategic reasoning of multi-agent systems and their environments. We study a new family of graph games which combine stochastic environmental uncertainties and auction-based interactions among the agents, formalized as bidding games on (finite) Markov decision processes (MDP). Normally, on MDPs, a single decision-maker chooses a sequence of actions, producing a probability distribution over infinite paths. In bidding games on MDPs, two players -- called the reachability and safety players -- bid for the privilege of choosing the next action at each step. The reachability player's goal is to maximize the probability of reaching a target vertex, whereas the safety player's goal is to minimize it. These games generalize traditional bidding games on graphs, and the existing analysis techniques do not extend. For instance, the central property of traditional bidding games is the existence of a threshold budget, which is a necessary and sufficient budget to guarantee winning for the reachability player. For MDPs, the threshold becomes a relation between the budgets and probabilities of reaching the target. We devise value-iteration algorithms that approximate thresholds and optimal policies for general MDPs, and compute the exact solutions for acyclic MDPs, and show that finding thresholds is at least as hard as solving simple-stochastic games.

Synthesis of Hierarchical Controllers Based on Deep Reinforcement Learning Policies

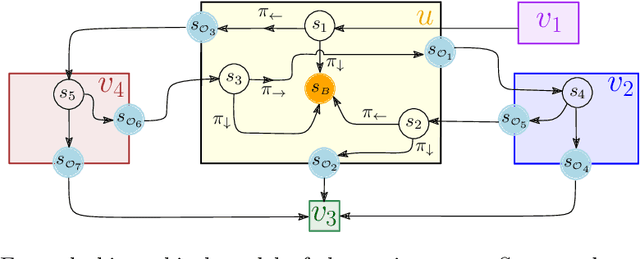
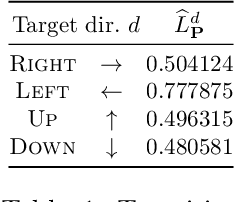
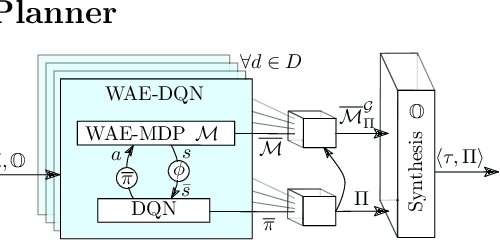
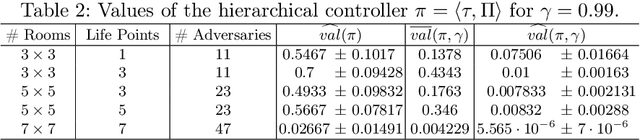
We propose a novel approach to the problem of controller design for environments modeled as Markov decision processes (MDPs). Specifically, we consider a hierarchical MDP a graph with each vertex populated by an MDP called a "room". We first apply deep reinforcement learning (DRL) to obtain low-level policies for each room, scaling to large rooms of unknown structure. We then apply reactive synthesis to obtain a high-level planner that chooses which low-level policy to execute in each room. The central challenge in synthesizing the planner is the need for modeling rooms. We address this challenge by developing a DRL procedure to train concise "latent" policies together with PAC guarantees on their performance. Unlike previous approaches, ours circumvents a model distillation step. Our approach combats sparse rewards in DRL and enables reusability of low-level policies. We demonstrate feasibility in a case study involving agent navigation amid moving obstacles.

Auction-Based Scheduling

Many sequential decision-making tasks require satisfaction of multiple, partially contradictory objectives. Existing approaches are monolithic, namely all objectives are fulfilled using a single policy, which is a function that selects a sequence of actions. We present auction-based scheduling, a modular framework for multi-objective decision-making problems. Each objective is fulfilled using a separate policy, and the policies can be independently created, modified, and replaced. Understandably, different policies with conflicting goals may choose conflicting actions at a given time. In order to resolve conflicts, and compose policies, we employ a novel auction-based mechanism. We allocate a bounded budget to each policy, and at each step, the policies simultaneously bid from their available budgets for the privilege of being scheduled and choosing an action. Policies express their scheduling urgency using their bids and the bounded budgets ensure long-run scheduling fairness. We lay the foundations of auction-based scheduling using path planning problems on finite graphs with two temporal objectives. We present decentralized algorithms to synthesize a pair of policies, their initially allocated budgets, and bidding strategies. We consider three categories of decentralized synthesis problems, parameterized by the assumptions that the policies make on each other: (a) strong synthesis, with no assumptions and strongest guarantees, (b) assume-admissible synthesis, with weakest rationality assumptions, and (c) assume-guarantee synthesis, with explicit contract-based assumptions. For reachability objectives, we show that, surprisingly, decentralized assume-admissible synthesis is always possible when the out-degrees of all vertices are at most two.

Reachability Poorman Discrete-Bidding Games

We consider {\em bidding games}, a class of two-player zero-sum {\em graph games}. The game proceeds as follows. Both players have bounded budgets. A token is placed on a vertex of a graph, in each turn the players simultaneously submit bids, and the higher bidder moves the token, where we break bidding ties in favor of Player 1. Player 1 wins the game iff the token visits a designated target vertex. We consider, for the first time, {\em poorman discrete-bidding} in which the granularity of the bids is restricted and the higher bid is paid to the bank. Previous work either did not impose granularity restrictions or considered {\em Richman} bidding (bids are paid to the opponent). While the latter mechanisms are technically more accessible, the former is more appealing from a practical standpoint. Our study focuses on {\em threshold budgets}, which is the necessary and sufficient initial budget required for Player 1 to ensure winning against a given Player 2 budget. We first show existence of thresholds. In DAGs, we show that threshold budgets can be approximated with error bounds by thresholds under continuous-bidding and that they exhibit a periodic behavior. We identify closed-form solutions in special cases. We implement and experiment with an algorithm to find threshold budgets.

ASQ-IT: Interactive Explanations for Reinforcement-Learning Agents

As reinforcement learning methods increasingly amass accomplishments, the need for comprehending their solutions becomes more crucial. Most explainable reinforcement learning (XRL) methods generate a static explanation depicting their developers' intuition of what should be explained and how. In contrast, literature from the social sciences proposes that meaningful explanations are structured as a dialog between the explainer and the explainee, suggesting a more active role for the user and her communication with the agent. In this paper, we present ASQ-IT -- an interactive tool that presents video clips of the agent acting in its environment based on queries given by the user that describe temporal properties of behaviors of interest. Our approach is based on formal methods: queries in ASQ-IT's user interface map to a fragment of Linear Temporal Logic over finite traces (LTLf), which we developed, and our algorithm for query processing is based on automata theory. User studies show that end-users can understand and formulate queries in ASQ-IT, and that using ASQ-IT assists users in identifying faulty agent behaviors.

Formal Methods with a Touch of Magic

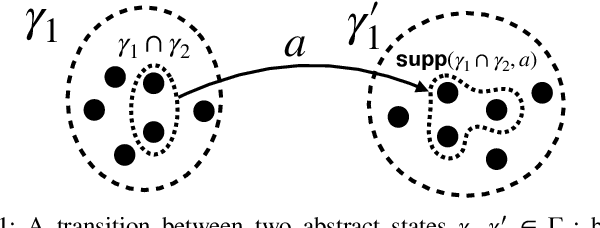
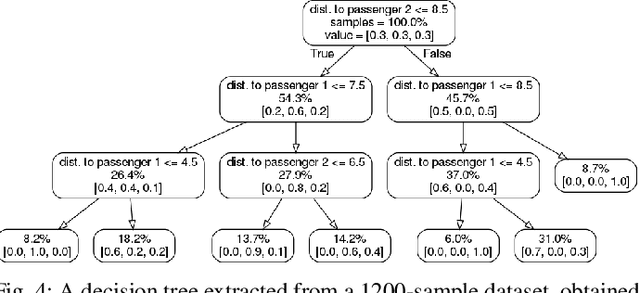
Machine learning and formal methods have complimentary benefits and drawbacks. In this work, we address the controller-design problem with a combination of techniques from both fields. The use of black-box neural networks in deep reinforcement learning (deep RL) poses a challenge for such a combination. Instead of reasoning formally about the output of deep RL, which we call the {\em wizard}, we extract from it a decision-tree based model, which we refer to as the {\em magic book}. Using the extracted model as an intermediary, we are able to handle problems that are infeasible for either deep RL or formal methods by themselves. First, we suggest, for the first time, combining a magic book in a synthesis procedure. We synthesize a stand-alone correct-by-design controller that enjoys the favorable performance of RL. Second, we incorporate a magic book in a bounded model checking (BMC) procedure. BMC allows us to find numerous traces of the plant under the control of the wizard, which a user can use to increase the trustworthiness of the wizard and direct further training.

All-Pay Bidding Games on Graphs

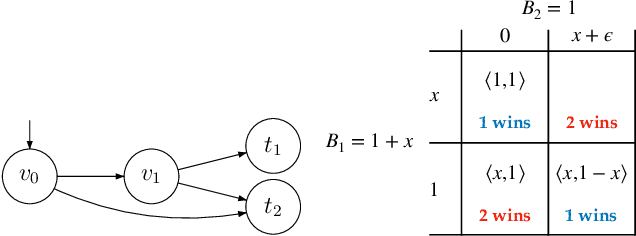
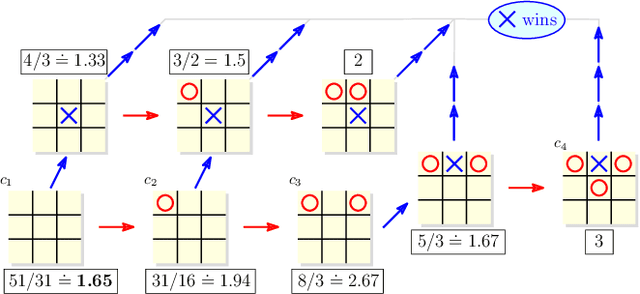
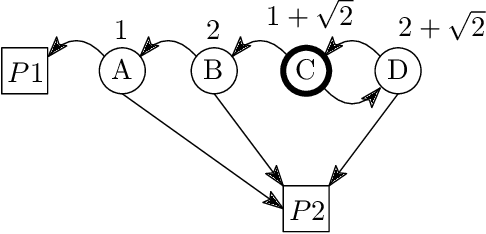
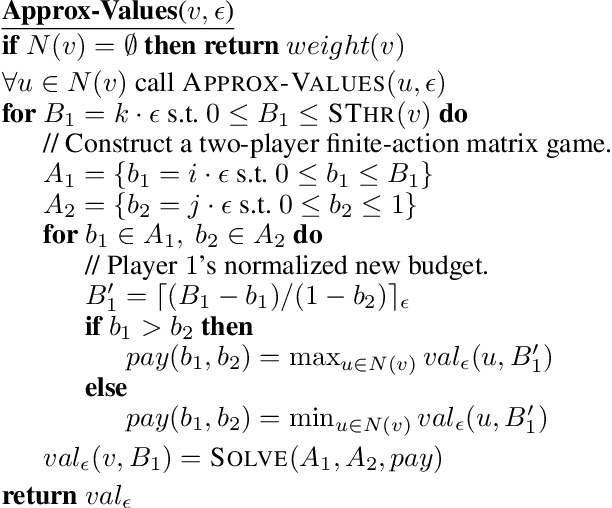
In this paper we introduce and study {\em all-pay bidding games}, a class of two player, zero-sum games on graphs. The game proceeds as follows. We place a token on some vertex in the graph and assign budgets to the two players. Each turn, each player submits a sealed legal bid (non-negative and below their remaining budget), which is deducted from their budget and the highest bidder moves the token onto an adjacent vertex. The game ends once a sink is reached, and \PO pays \PT the outcome that is associated with the sink. The players attempt to maximize their expected outcome. Our games model settings where effort (of no inherent value) needs to be invested in an ongoing and stateful manner. On the negative side, we show that even in simple games on DAGs, optimal strategies may require a distribution over bids with infinite support. A central quantity in bidding games is the {\em ratio} of the players budgets. On the positive side, we show a simple FPTAS for DAGs, that, for each budget ratio, outputs an approximation for the optimal strategy for that ratio. We also implement it, show that it performs well, and suggests interesting properties of these games. Then, given an outcome $c$, we show an algorithm for finding the necessary and sufficient initial ratio for guaranteeing outcome $c$ with probability~$1$ and a strategy ensuring such. Finally, while the general case has not previously been studied, solving the specific game in which \PO wins iff he wins the first two auctions, has been long stated as an open question, which we solve.