All-Pay Bidding Games on Graphs
Paper and Code
Nov 19, 2019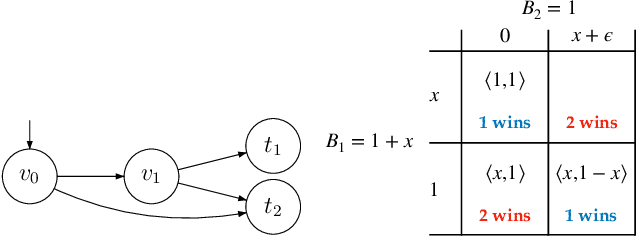
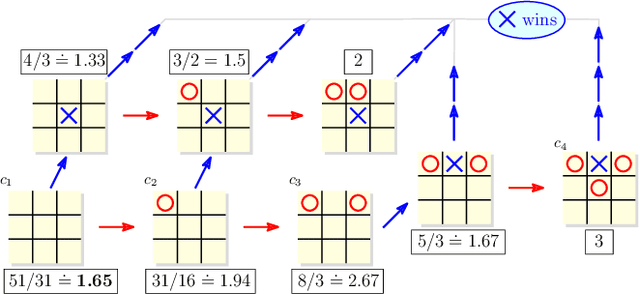
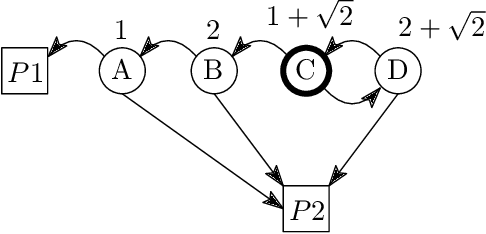
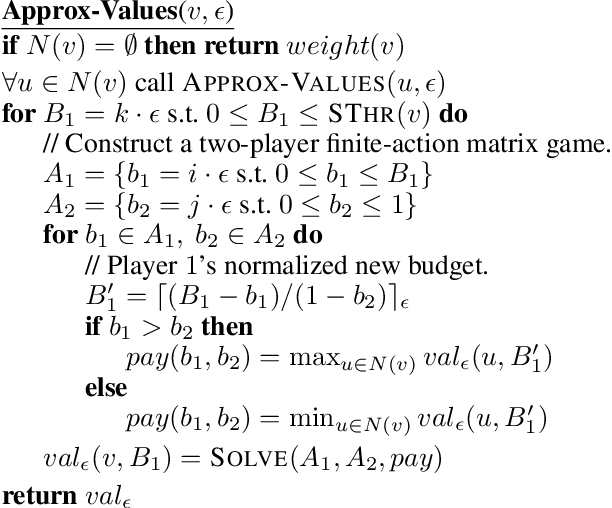
In this paper we introduce and study {\em all-pay bidding games}, a class of two player, zero-sum games on graphs. The game proceeds as follows. We place a token on some vertex in the graph and assign budgets to the two players. Each turn, each player submits a sealed legal bid (non-negative and below their remaining budget), which is deducted from their budget and the highest bidder moves the token onto an adjacent vertex. The game ends once a sink is reached, and \PO pays \PT the outcome that is associated with the sink. The players attempt to maximize their expected outcome. Our games model settings where effort (of no inherent value) needs to be invested in an ongoing and stateful manner. On the negative side, we show that even in simple games on DAGs, optimal strategies may require a distribution over bids with infinite support. A central quantity in bidding games is the {\em ratio} of the players budgets. On the positive side, we show a simple FPTAS for DAGs, that, for each budget ratio, outputs an approximation for the optimal strategy for that ratio. We also implement it, show that it performs well, and suggests interesting properties of these games. Then, given an outcome $c$, we show an algorithm for finding the necessary and sufficient initial ratio for guaranteeing outcome $c$ with probability~$1$ and a strategy ensuring such. Finally, while the general case has not previously been studied, solving the specific game in which \PO wins iff he wins the first two auctions, has been long stated as an open question, which we solve.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge