All-Pay Bidding Games on Graphs

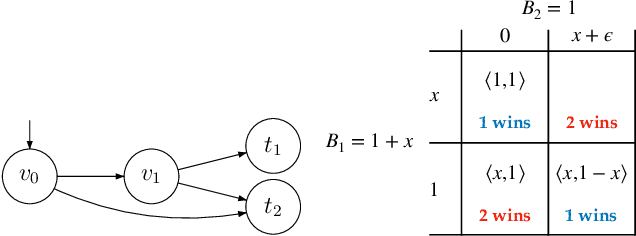
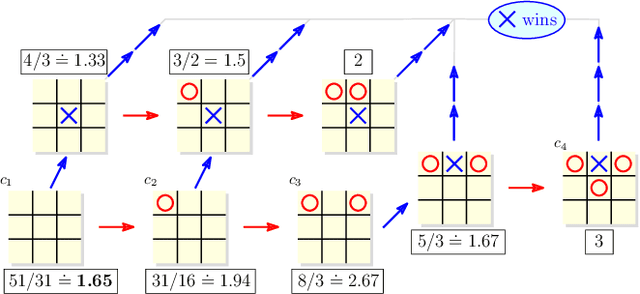
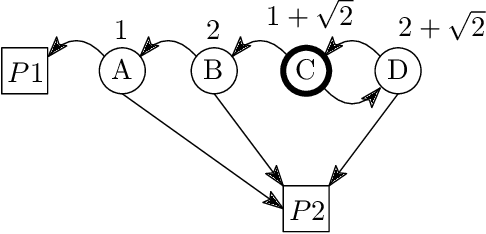
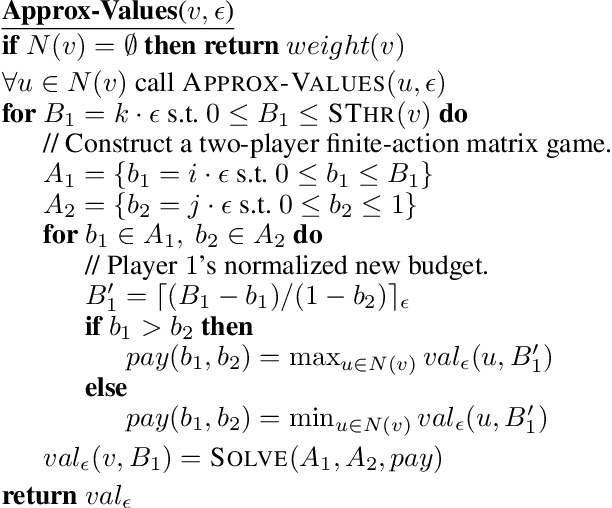
In this paper we introduce and study {\em all-pay bidding games}, a class of two player, zero-sum games on graphs. The game proceeds as follows. We place a token on some vertex in the graph and assign budgets to the two players. Each turn, each player submits a sealed legal bid (non-negative and below their remaining budget), which is deducted from their budget and the highest bidder moves the token onto an adjacent vertex. The game ends once a sink is reached, and \PO pays \PT the outcome that is associated with the sink. The players attempt to maximize their expected outcome. Our games model settings where effort (of no inherent value) needs to be invested in an ongoing and stateful manner. On the negative side, we show that even in simple games on DAGs, optimal strategies may require a distribution over bids with infinite support. A central quantity in bidding games is the {\em ratio} of the players budgets. On the positive side, we show a simple FPTAS for DAGs, that, for each budget ratio, outputs an approximation for the optimal strategy for that ratio. We also implement it, show that it performs well, and suggests interesting properties of these games. Then, given an outcome $c$, we show an algorithm for finding the necessary and sufficient initial ratio for guaranteeing outcome $c$ with probability~$1$ and a strategy ensuring such. Finally, while the general case has not previously been studied, solving the specific game in which \PO wins iff he wins the first two auctions, has been long stated as an open question, which we solve.

Faster Monte-Carlo Algorithms for Fixation Probability of the Moran Process on Undirected Graphs

Evolutionary graph theory studies the evolutionary dynamics in a population structure given as a connected graph. Each node of the graph represents an individual of the population, and edges determine how offspring are placed. We consider the classical birth-death Moran process where there are two types of individuals, namely, the residents with fitness 1 and mutants with fitness r. The fitness indicates the reproductive strength. The evolutionary dynamics happens as follows: in the initial step, in a population of all resident individuals a mutant is introduced, and then at each step, an individual is chosen proportional to the fitness of its type to reproduce, and the offspring replaces a neighbor uniformly at random. The process stops when all individuals are either residents or mutants. The probability that all individuals in the end are mutants is called the fixation probability. We present faster polynomial-time Monte-Carlo algorithms for finidng the fixation probability on undirected graphs. Our algorithms are always at least a factor O(n^2/log n) faster as compared to the previous algorithms, where n is the number of nodes, and is polynomial even if r is given in binary. We also present lower bounds showing that the upper bound on the expected number of effective steps we present is asymptotically tight for undirected graphs.

Generalized Risk-Aversion in Stochastic Multi-Armed Bandits

We consider the problem of minimizing the regret in stochastic multi-armed bandit, when the measure of goodness of an arm is not the mean return, but some general function of the mean and the variance.We characterize the conditions under which learning is possible and present examples for which no natural algorithm can achieve sublinear regret.