Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Reachability Poorman Discrete-Bidding Games

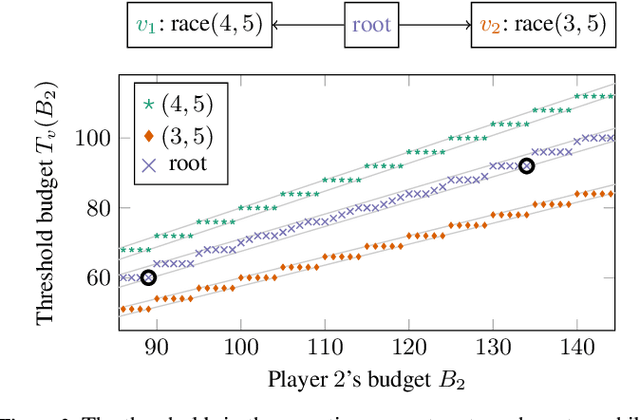
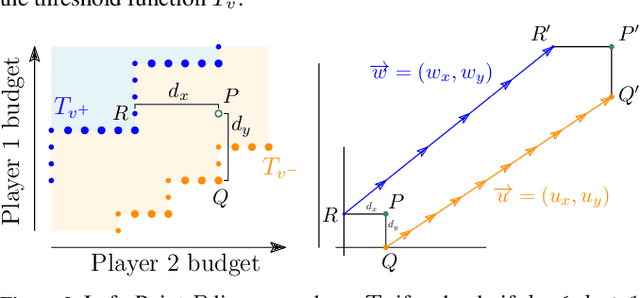
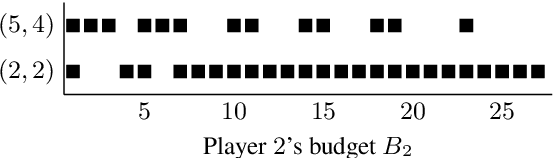
We consider {\em bidding games}, a class of two-player zero-sum {\em graph games}. The game proceeds as follows. Both players have bounded budgets. A token is placed on a vertex of a graph, in each turn the players simultaneously submit bids, and the higher bidder moves the token, where we break bidding ties in favor of Player 1. Player 1 wins the game iff the token visits a designated target vertex. We consider, for the first time, {\em poorman discrete-bidding} in which the granularity of the bids is restricted and the higher bid is paid to the bank. Previous work either did not impose granularity restrictions or considered {\em Richman} bidding (bids are paid to the opponent). While the latter mechanisms are technically more accessible, the former is more appealing from a practical standpoint. Our study focuses on {\em threshold budgets}, which is the necessary and sufficient initial budget required for Player 1 to ensure winning against a given Player 2 budget. We first show existence of thresholds. In DAGs, we show that threshold budgets can be approximated with error bounds by thresholds under continuous-bidding and that they exhibit a periodic behavior. We identify closed-form solutions in special cases. We implement and experiment with an algorithm to find threshold budgets.

All-Pay Bidding Games on Graphs

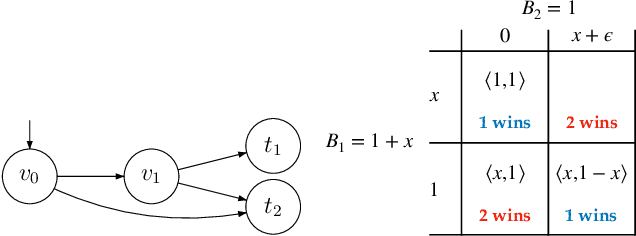
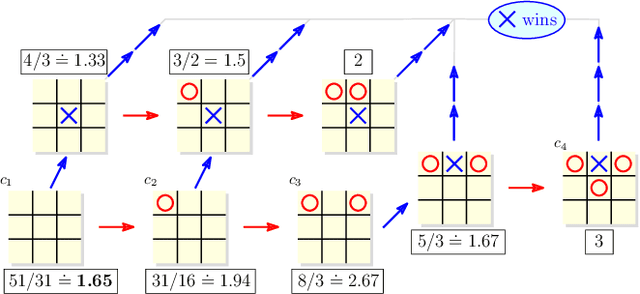
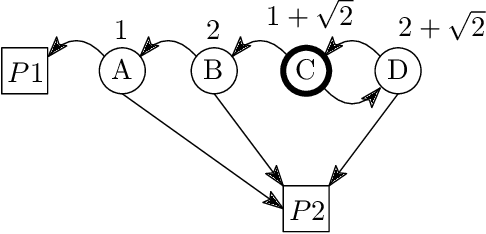
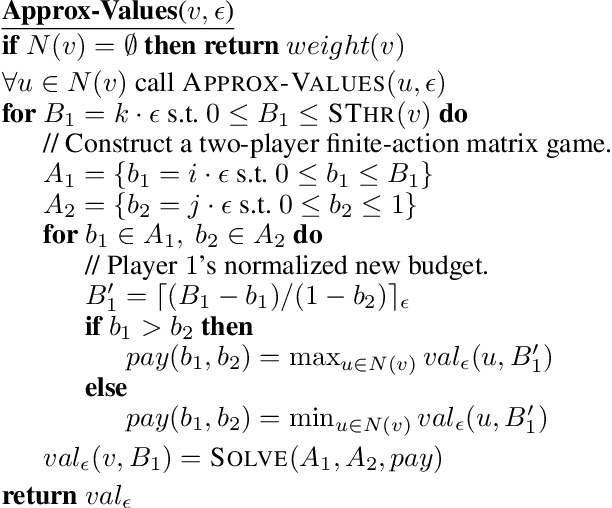
In this paper we introduce and study {\em all-pay bidding games}, a class of two player, zero-sum games on graphs. The game proceeds as follows. We place a token on some vertex in the graph and assign budgets to the two players. Each turn, each player submits a sealed legal bid (non-negative and below their remaining budget), which is deducted from their budget and the highest bidder moves the token onto an adjacent vertex. The game ends once a sink is reached, and \PO pays \PT the outcome that is associated with the sink. The players attempt to maximize their expected outcome. Our games model settings where effort (of no inherent value) needs to be invested in an ongoing and stateful manner. On the negative side, we show that even in simple games on DAGs, optimal strategies may require a distribution over bids with infinite support. A central quantity in bidding games is the {\em ratio} of the players budgets. On the positive side, we show a simple FPTAS for DAGs, that, for each budget ratio, outputs an approximation for the optimal strategy for that ratio. We also implement it, show that it performs well, and suggests interesting properties of these games. Then, given an outcome $c$, we show an algorithm for finding the necessary and sufficient initial ratio for guaranteeing outcome $c$ with probability~$1$ and a strategy ensuring such. Finally, while the general case has not previously been studied, solving the specific game in which \PO wins iff he wins the first two auctions, has been long stated as an open question, which we solve.