Bidding Games on Markov Decision Processes with Quantitative Reachability Objectives

Graph games are fundamental in strategic reasoning of multi-agent systems and their environments. We study a new family of graph games which combine stochastic environmental uncertainties and auction-based interactions among the agents, formalized as bidding games on (finite) Markov decision processes (MDP). Normally, on MDPs, a single decision-maker chooses a sequence of actions, producing a probability distribution over infinite paths. In bidding games on MDPs, two players -- called the reachability and safety players -- bid for the privilege of choosing the next action at each step. The reachability player's goal is to maximize the probability of reaching a target vertex, whereas the safety player's goal is to minimize it. These games generalize traditional bidding games on graphs, and the existing analysis techniques do not extend. For instance, the central property of traditional bidding games is the existence of a threshold budget, which is a necessary and sufficient budget to guarantee winning for the reachability player. For MDPs, the threshold becomes a relation between the budgets and probabilities of reaching the target. We devise value-iteration algorithms that approximate thresholds and optimal policies for general MDPs, and compute the exact solutions for acyclic MDPs, and show that finding thresholds is at least as hard as solving simple-stochastic games.

Auction-Based Scheduling

Many sequential decision-making tasks require satisfaction of multiple, partially contradictory objectives. Existing approaches are monolithic, namely all objectives are fulfilled using a single policy, which is a function that selects a sequence of actions. We present auction-based scheduling, a modular framework for multi-objective decision-making problems. Each objective is fulfilled using a separate policy, and the policies can be independently created, modified, and replaced. Understandably, different policies with conflicting goals may choose conflicting actions at a given time. In order to resolve conflicts, and compose policies, we employ a novel auction-based mechanism. We allocate a bounded budget to each policy, and at each step, the policies simultaneously bid from their available budgets for the privilege of being scheduled and choosing an action. Policies express their scheduling urgency using their bids and the bounded budgets ensure long-run scheduling fairness. We lay the foundations of auction-based scheduling using path planning problems on finite graphs with two temporal objectives. We present decentralized algorithms to synthesize a pair of policies, their initially allocated budgets, and bidding strategies. We consider three categories of decentralized synthesis problems, parameterized by the assumptions that the policies make on each other: (a) strong synthesis, with no assumptions and strongest guarantees, (b) assume-admissible synthesis, with weakest rationality assumptions, and (c) assume-guarantee synthesis, with explicit contract-based assumptions. For reachability objectives, we show that, surprisingly, decentralized assume-admissible synthesis is always possible when the out-degrees of all vertices are at most two.

Reachability Poorman Discrete-Bidding Games

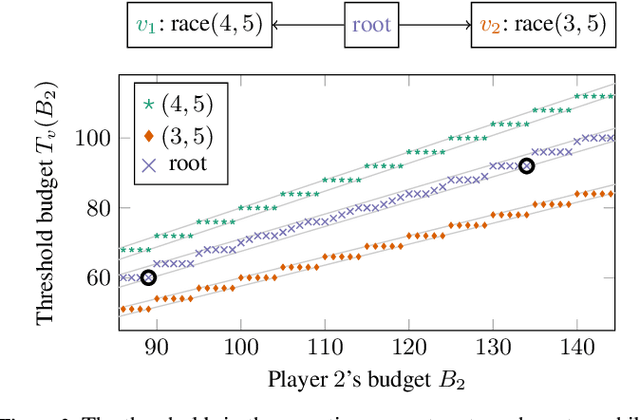
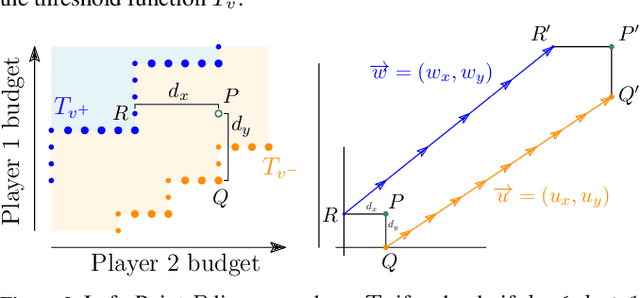
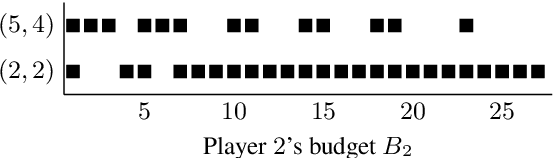
We consider {\em bidding games}, a class of two-player zero-sum {\em graph games}. The game proceeds as follows. Both players have bounded budgets. A token is placed on a vertex of a graph, in each turn the players simultaneously submit bids, and the higher bidder moves the token, where we break bidding ties in favor of Player 1. Player 1 wins the game iff the token visits a designated target vertex. We consider, for the first time, {\em poorman discrete-bidding} in which the granularity of the bids is restricted and the higher bid is paid to the bank. Previous work either did not impose granularity restrictions or considered {\em Richman} bidding (bids are paid to the opponent). While the latter mechanisms are technically more accessible, the former is more appealing from a practical standpoint. Our study focuses on {\em threshold budgets}, which is the necessary and sufficient initial budget required for Player 1 to ensure winning against a given Player 2 budget. We first show existence of thresholds. In DAGs, we show that threshold budgets can be approximated with error bounds by thresholds under continuous-bidding and that they exhibit a periodic behavior. We identify closed-form solutions in special cases. We implement and experiment with an algorithm to find threshold budgets.