Pierre H. Richemond
ShiQ: Bringing back Bellman to LLMs
May 16, 2025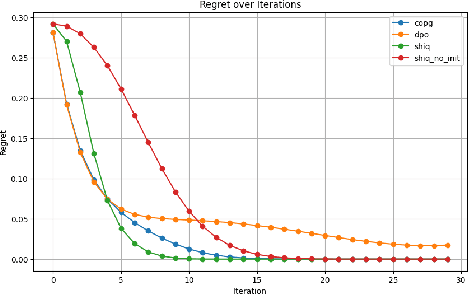
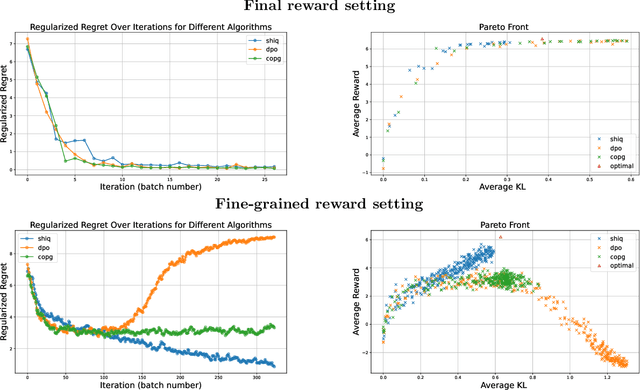

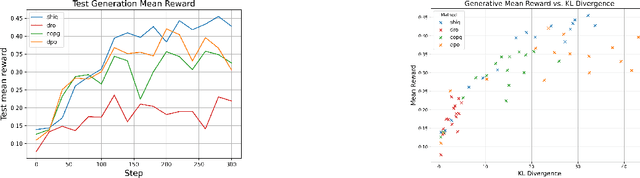
Abstract:The fine-tuning of pre-trained large language models (LLMs) using reinforcement learning (RL) is generally formulated as direct policy optimization. This approach was naturally favored as it efficiently improves a pretrained LLM, seen as an initial policy. Another RL paradigm, Q-learning methods, has received far less attention in the LLM community while demonstrating major success in various non-LLM RL tasks. In particular, Q-learning effectiveness comes from its sample efficiency and ability to learn offline, which is particularly valuable given the high computational cost of sampling with LLMs. However, naively applying a Q-learning-style update to the model's logits is ineffective due to the specificity of LLMs. Our core contribution is to derive theoretically grounded loss functions from Bellman equations to adapt Q-learning methods to LLMs. To do so, we carefully adapt insights from the RL literature to account for LLM-specific characteristics, ensuring that the logits become reliable Q-value estimates. We then use this loss to build a practical algorithm, ShiQ for Shifted-Q, that supports off-policy, token-wise learning while remaining simple to implement. Finally, we evaluate ShiQ on both synthetic data and real-world benchmarks, e.g., UltraFeedback and BFCL-V3, demonstrating its effectiveness in both single-turn and multi-turn LLM settings
The Edge of Orthogonality: A Simple View of What Makes BYOL Tick
Feb 09, 2023Abstract:Self-predictive unsupervised learning methods such as BYOL or SimSiam have shown impressive results, and counter-intuitively, do not collapse to trivial representations. In this work, we aim at exploring the simplest possible mathematical arguments towards explaining the underlying mechanisms behind self-predictive unsupervised learning. We start with the observation that those methods crucially rely on the presence of a predictor network (and stop-gradient). With simple linear algebra, we show that when using a linear predictor, the optimal predictor is close to an orthogonal projection, and propose a general framework based on orthonormalization that enables to interpret and give intuition on why BYOL works. In addition, this framework demonstrates the crucial role of the exponential moving average and stop-gradient operator in BYOL as an efficient orthonormalization mechanism. We use these insights to propose four new \emph{closed-form predictor} variants of BYOL to support our analysis. Our closed-form predictors outperform standard linear trainable predictor BYOL at $100$ and $300$ epochs (top-$1$ linear accuracy on ImageNet).
SemPPL: Predicting pseudo-labels for better contrastive representations
Jan 12, 2023Abstract:Learning from large amounts of unsupervised data and a small amount of supervision is an important open problem in computer vision. We propose a new semi-supervised learning method, Semantic Positives via Pseudo-Labels (SemPPL), that combines labelled and unlabelled data to learn informative representations. Our method extends self-supervised contrastive learning -- where representations are shaped by distinguishing whether two samples represent the same underlying datum (positives) or not (negatives) -- with a novel approach to selecting positives. To enrich the set of positives, we leverage the few existing ground-truth labels to predict the missing ones through a $k$-nearest neighbours classifier by using the learned embeddings of the labelled data. We thus extend the set of positives with datapoints having the same pseudo-label and call these semantic positives. We jointly learn the representation and predict bootstrapped pseudo-labels. This creates a reinforcing cycle. Strong initial representations enable better pseudo-label predictions which then improve the selection of semantic positives and lead to even better representations. SemPPL outperforms competing semi-supervised methods setting new state-of-the-art performance of $68.5\%$ and $76\%$ top-$1$ accuracy when using a ResNet-$50$ and training on $1\%$ and $10\%$ of labels on ImageNet, respectively. Furthermore, when using selective kernels, SemPPL significantly outperforms previous state-of-the-art achieving $72.3\%$ and $78.3\%$ top-$1$ accuracy on ImageNet with $1\%$ and $10\%$ labels, respectively, which improves absolute $+7.8\%$ and $+6.2\%$ over previous work. SemPPL also exhibits state-of-the-art performance over larger ResNet models as well as strong robustness, out-of-distribution and transfer performance.
Continuous diffusion for categorical data
Dec 15, 2022



Abstract:Diffusion models have quickly become the go-to paradigm for generative modelling of perceptual signals (such as images and sound) through iterative refinement. Their success hinges on the fact that the underlying physical phenomena are continuous. For inherently discrete and categorical data such as language, various diffusion-inspired alternatives have been proposed. However, the continuous nature of diffusion models conveys many benefits, and in this work we endeavour to preserve it. We propose CDCD, a framework for modelling categorical data with diffusion models that are continuous both in time and input space. We demonstrate its efficacy on several language modelling tasks.
Categorical SDEs with Simplex Diffusion
Oct 26, 2022Abstract:Diffusion models typically operate in the standard framework of generative modelling by producing continuously-valued datapoints. To this end, they rely on a progressive Gaussian smoothing of the original data distribution, which admits an SDE interpretation involving increments of a standard Brownian motion. However, some applications such as text generation or reinforcement learning might naturally be better served by diffusing categorical-valued data, i.e., lifting the diffusion to a space of probability distributions. To this end, this short theoretical note proposes Simplex Diffusion, a means to directly diffuse datapoints located on an n-dimensional probability simplex. We show how this relates to the Dirichlet distribution on the simplex and how the analogous SDE is realized thanks to a multi-dimensional Cox-Ingersoll-Ross process (abbreviated as CIR), previously used in economics and mathematical finance. Finally, we make remarks as to the numerical implementation of trajectories of the CIR process, and discuss some limitations of our approach.
Zipfian environments for Reinforcement Learning
Mar 15, 2022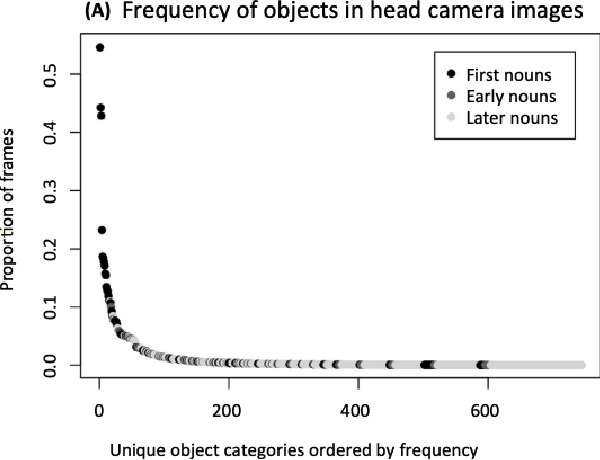

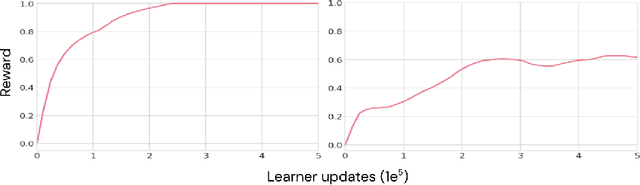

Abstract:As humans and animals learn in the natural world, they encounter distributions of entities, situations and events that are far from uniform. Typically, a relatively small set of experiences are encountered frequently, while many important experiences occur only rarely. The highly-skewed, heavy-tailed nature of reality poses particular learning challenges that humans and animals have met by evolving specialised memory systems. By contrast, most popular RL environments and benchmarks involve approximately uniform variation of properties, objects, situations or tasks. How will RL algorithms perform in worlds (like ours) where the distribution of environment features is far less uniform? To explore this question, we develop three complementary RL environments where the agent's experience varies according to a Zipfian (discrete power law) distribution. On these benchmarks, we find that standard Deep RL architectures and algorithms acquire useful knowledge of common situations and tasks, but fail to adequately learn about rarer ones. To understand this failure better, we explore how different aspects of current approaches may be adjusted to help improve performance on rare events, and show that the RL objective function, the agent's memory system and self-supervised learning objectives can all influence an agent's ability to learn from uncommon experiences. Together, these results show that learning robustly from skewed experience is a critical challenge for applying Deep RL methods beyond simulations or laboratories, and our Zipfian environments provide a basis for measuring future progress towards this goal.
BYOL works even without batch statistics
Oct 20, 2020

Abstract:Bootstrap Your Own Latent (BYOL) is a self-supervised learning approach for image representation. From an augmented view of an image, BYOL trains an online network to predict a target network representation of a different augmented view of the same image. Unlike contrastive methods, BYOL does not explicitly use a repulsion term built from negative pairs in its training objective. Yet, it avoids collapse to a trivial, constant representation. Thus, it has recently been hypothesized that batch normalization (BN) is critical to prevent collapse in BYOL. Indeed, BN flows gradients across batch elements, and could leak information about negative views in the batch, which could act as an implicit negative (contrastive) term. However, we experimentally show that replacing BN with a batch-independent normalization scheme (namely, a combination of group normalization and weight standardization) achieves performance comparable to vanilla BYOL ($73.9\%$ vs. $74.3\%$ top-1 accuracy under the linear evaluation protocol on ImageNet with ResNet-$50$). Our finding disproves the hypothesis that the use of batch statistics is a crucial ingredient for BYOL to learn useful representations.
Bootstrap Your Own Latent: A New Approach to Self-Supervised Learning
Jun 13, 2020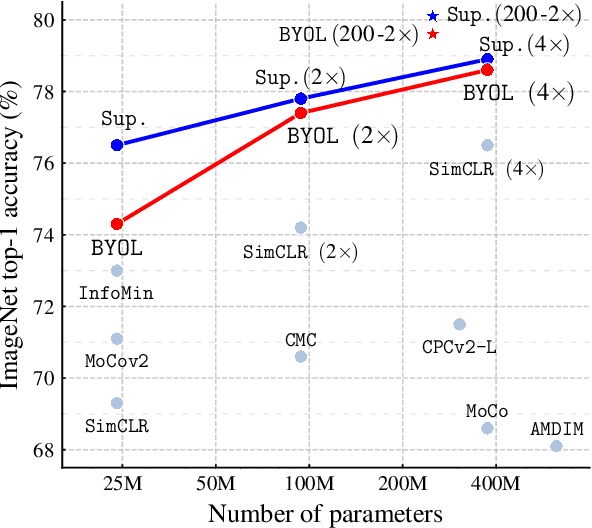

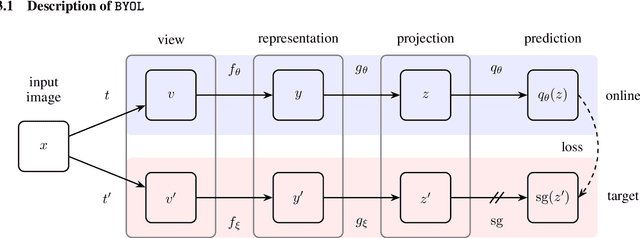
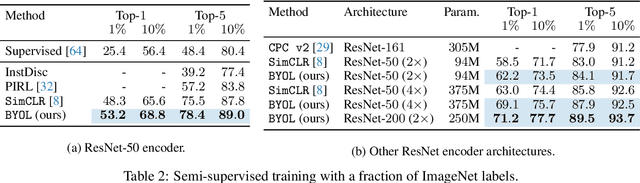
Abstract:We introduce Bootstrap Your Own Latent (BYOL), a new approach to self-supervised image representation learning. BYOL relies on two neural networks, referred to as online and target networks, that interact and learn from each other. From an augmented view of an image, we train the online network to predict the target network representation of the same image under a different augmented view. At the same time, we update the target network with a slow-moving average of the online network. While state-of-the art methods intrinsically rely on negative pairs, BYOL achieves a new state of the art without them. BYOL reaches $74.3\%$ top-1 classification accuracy on ImageNet using the standard linear evaluation protocol with a ResNet-50 architecture and $79.6\%$ with a larger ResNet. We show that BYOL performs on par or better than the current state of the art on both transfer and semi-supervised benchmarks.
Biologically inspired architectures for sample-efficient deep reinforcement learning
Nov 25, 2019

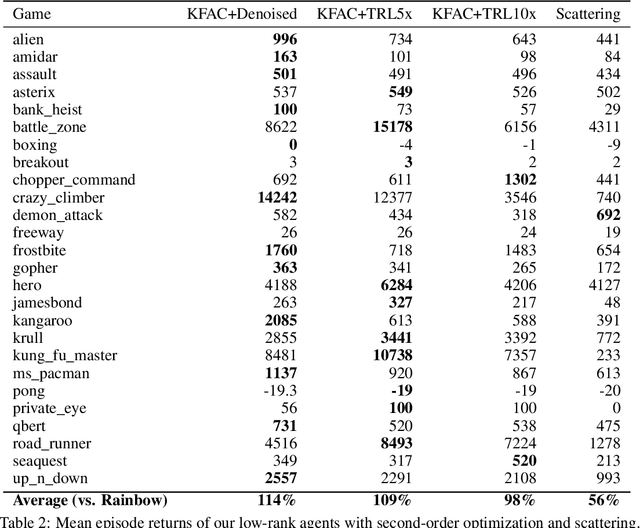
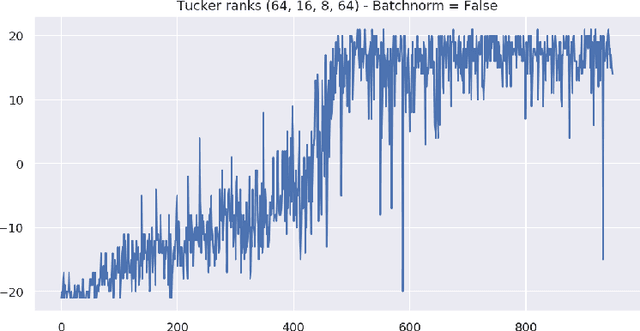
Abstract:Deep reinforcement learning requires a heavy price in terms of sample efficiency and overparameterization in the neural networks used for function approximation. In this work, we use tensor factorization in order to learn more compact representation for reinforcement learning policies. We show empirically that in the low-data regime, it is possible to learn online policies with 2 to 10 times less total coefficients, with little to no loss of performance. We also leverage progress in second order optimization, and use the theory of wavelet scattering to further reduce the number of learned coefficients, by foregoing learning the topmost convolutional layer filters altogether. We evaluate our results on the Atari suite against recent baseline algorithms that represent the state-of-the-art in data efficiency, and get comparable results with an order of magnitude gain in weight parsimony.
Static Activation Function Normalization
May 03, 2019



Abstract:Recent seminal work at the intersection of deep neural networks practice and random matrix theory has linked the convergence speed and robustness of these networks with the combination of random weight initialization and nonlinear activation function in use. Building on those principles, we introduce a process to transform an existing activation function into another one with better properties. We term such transform \emph{static activation normalization}. More specifically we focus on this normalization applied to the ReLU unit, and show empirically that it significantly promotes convergence robustness, maximum training depth, and anytime performance. We verify these claims by examining empirical eigenvalue distributions of networks trained with those activations. Our static activation normalization provides a first step towards giving benefits similar in spirit to schemes like batch normalization, but without computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge