Biologically inspired architectures for sample-efficient deep reinforcement learning
Paper and Code
Nov 25, 2019

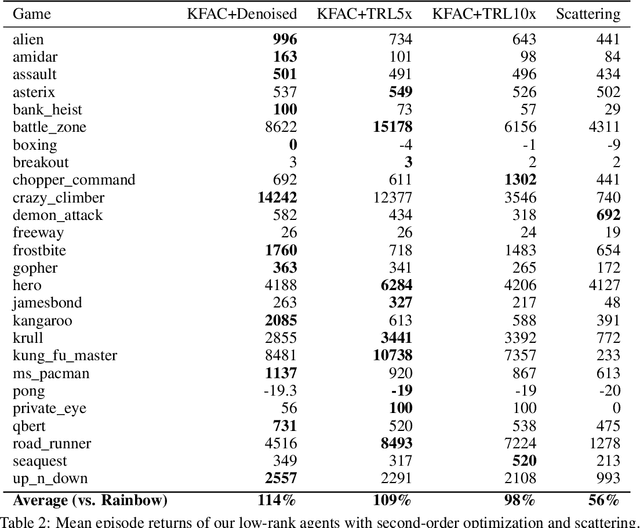
Deep reinforcement learning requires a heavy price in terms of sample efficiency and overparameterization in the neural networks used for function approximation. In this work, we use tensor factorization in order to learn more compact representation for reinforcement learning policies. We show empirically that in the low-data regime, it is possible to learn online policies with 2 to 10 times less total coefficients, with little to no loss of performance. We also leverage progress in second order optimization, and use the theory of wavelet scattering to further reduce the number of learned coefficients, by foregoing learning the topmost convolutional layer filters altogether. We evaluate our results on the Atari suite against recent baseline algorithms that represent the state-of-the-art in data efficiency, and get comparable results with an order of magnitude gain in weight parsimony.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge