Optimizing Expectation with Guarantees in POMDPs (Technical Report)
Paper and Code
Jan 29, 2017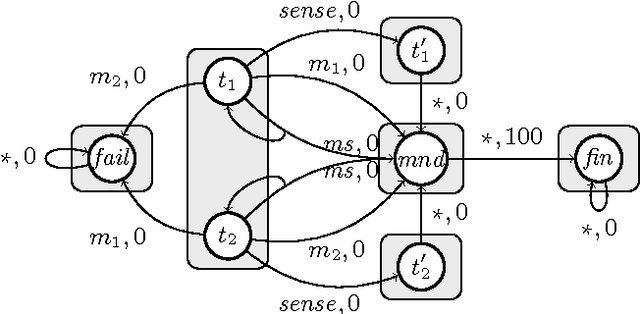
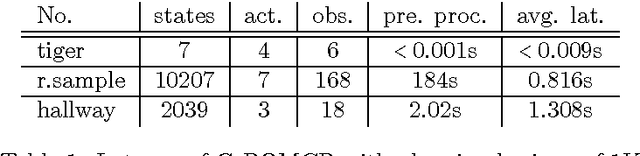
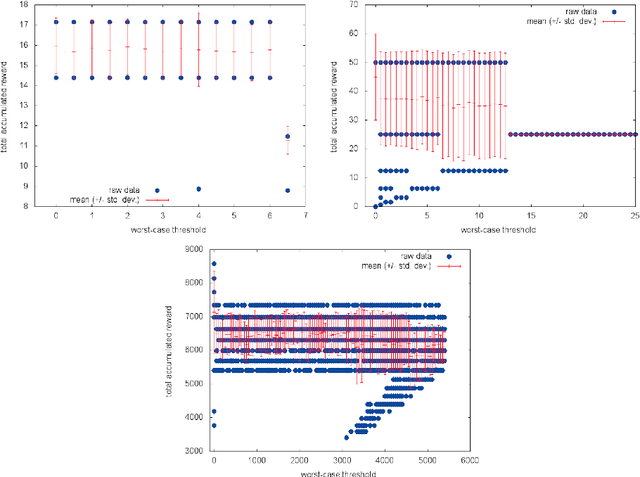
A standard objective in partially-observable Markov decision processes (POMDPs) is to find a policy that maximizes the expected discounted-sum payoff. However, such policies may still permit unlikely but highly undesirable outcomes, which is problematic especially in safety-critical applications. Recently, there has been a surge of interest in POMDPs where the goal is to maximize the probability to ensure that the payoff is at least a given threshold, but these approaches do not consider any optimization beyond satisfying this threshold constraint. In this work we go beyond both the "expectation" and "threshold" approaches and consider a "guaranteed payoff optimization (GPO)" problem for POMDPs, where we are given a threshold $t$ and the objective is to find a policy $\sigma$ such that a) each possible outcome of $\sigma$ yields a discounted-sum payoff of at least $t$, and b) the expected discounted-sum payoff of $\sigma$ is optimal (or near-optimal) among all policies satisfying a). We present a practical approach to tackle the GPO problem and evaluate it on standard POMDP benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge